§ 4. Основная теорема зубчатого зацепления.

Понятия о линии и полюсе зацепления. Профилирование зубьев

3.15. Для обеспечения нормальной работы пары зубчатых колес с по-:тоянным передаточным числом профили зубьев должны быть очерчены ~о кривым, подчиняющимся определенным законам. Эти законы вытека­ют из основной теоремы зацепления, сущность которой заключается в сле-гующем.

Пусть имеется пара зубчатых колес с центрами О₁ и О₂, вращающихся :эответственно с угловыми скоростями со, и со₂. На рис. 3.18, а показаны г сложения, которые последовательно занимает пара сопряженных (эволь-нгнтных) зубьев в процессе их зацепления; прямую О₁О₂ называют межосе-еой линией зубчатой передачи. Проведем в точках касания зубьев К₁, К₂,

а) б)

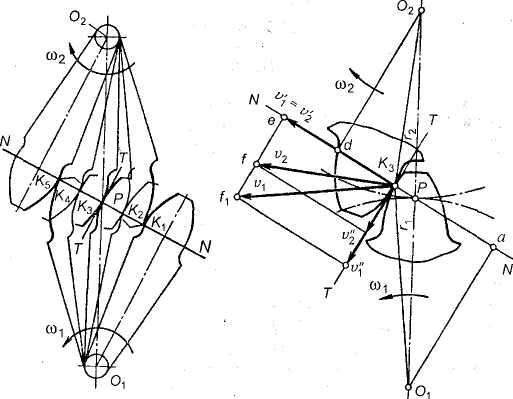
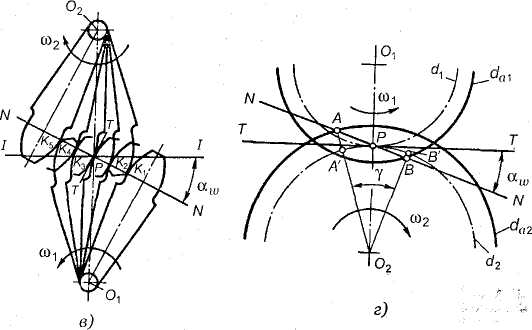
Рис. 3.18. Элементы зубчатого зацепления

К_г, ... общие нормали к профилям. Все эти нормали NN должны пересекать межосевую линию О₁ О₂ в постоянной точке Р. Эту точку называют полюсом зацепления; ее положение на межосевой линии определяется отношением уг­ловых скоростей колес, т. е. их отношением:

.

Основную теорему зацепления можно сформулировать так: общая нор­маль к профилям зубьев в точке их касания пересекает межосевую линию в точке Р, называемой полюсом зацепления и делящей межосевое расстояние не отрезки, обратно пропорционально угловым скоростям.

Следствие: для обеспечения постоянного передаточного отношения по­ложение полюса Р на линии центров должно быть постоянным.

3.16. В процессе работы сопряженных (эвольвентных) профилей точка их касания все время перемещается по прямой NN. Эту прямую называют линией зацепления.

Место (точку) входа в зацепление и выхода из него сопряженных зубь­ев можно определить при следующем геометрическом построении.

Возьмем произвольное межосевое расстояние О₁ О₂ (рис. 3.18, г) и раз­делим его в произвольном отношении O₂P/O₁P = и. Радиусами О₂Р и O₁P проведем начальные окружности зубчатых колес через точку Р, касатель­ную ТТ к этим окружностям и линию NN — нормаль к боковым поверхно­стям зубьев — под углом а_ω и касательной ТТ. Угол a_ω называют углом за­цепления; в СНГ а_ω принят 20°.

Примем произвольную высоту головки зубьев и проведем радиусами. равными 1/2d_a1 и 1/2d_a2, окружности выступов зубчатых колес (высота го­ловки зуба шестерни и колеса должна быть одинаковой). При направлении вращения колес, указанном на рисунке, зубья войдут в зацепление в точке А (точке пересечения нормали с окружностью выступов колеса) и выйду: из зацепления в точке В (точке пересечения нормали с окружностью вы­ступов шестерни).

Все точки касания сопряженных зубьев будут лежать на участке АВ ли­нии зацепления. Участок АВ называется рабочим участком линии зацепле­ния.

Необходимое условие непрерывности зацепления: дуга зацепления должна быть больше шага. В противном случае при выходе из зацепления одной пары зубьев вторая пара еще не войдет.

Длина линии зацепления q_a — отрезок линии зацепления, отсекаемы;: окружностями вершин зубьев сопряженных колес. Он определяет начало у. конец зацепления пары сопряженных зубьев. Длина зацепления — актив­ная часть линии зацепления.

Коэффициент торцового перекрытия ε_a — отношение длины линии за­цепления к шагу:

.

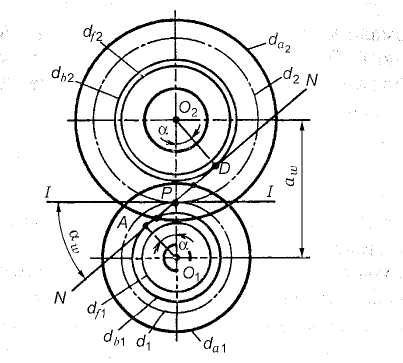
Рис. 3.19. Геометрические параметры зубчатой передачи

Можно ли увидеть на зубчатом колесе (рис. 3.19) линию зацепления NN и угол зацепления a_w или это только теоретически представляемые геометри­ческие элементы?

3.17. Полюс зацепления Р (см. рис. 3.18, б) сохраняет неизменное положе­ние на линии центров 0₁0₂. Следовательно, радиусы 0₁Р (r₁) и 0₂Р (r₂) также неизменны. Окружности радиусов r₁ и r₂ называют начальными (делитель­ными — см. шаг 3.13). При вращении зубчатых колес эти окружности пе­рекатываются одна по другой без скольжения, о чем свидетельствует ра­венство их окружных скоростей ω₁ r₁ = ω₂r₂ (см. доказательство основной теоремы зацепления). Теоретически боковые поверхности зубьев (профи­ли) могут быть очерчены любыми кривыми, удовлетворяющими основному закону зубчатого зацепления. Такие профили называют сопряженными. В современном машиностроении для построения сопряженных профилей применяют ограниченное число кривых.

Уточните основное условие для обеспечения постоянства передаточного числа зубчатой передачи.

3.18. Профили зубьев должны быть технологичными, т. е. такими, чтобы их можно было получить в производственных условиях наиболее простыми методами. Из теоретически возможных профилей преимущественное приме­ нение получили эвольвентные профили (см. рис. 3.18, б), так как такие про­ фили проще обработать и они обладают большими преимуществами. Эвольвентное зацепление предложено Эйлером более 200 лет назад. Это зацепление по сравнению с другими имеет следующие преимущества: при изменении межосевого расстояния не нарушается правильность их зацеп­ ления (не изменяется передаточное число); это зацепление может быть ис- тользовано и в сменных колесах.

В зацеплении М. Л. Новикова рабочие профили зубьев очерчены дуга­ми окружностей (рис. 3.20, 3.21). По сравнению с эвольвентными передачи : зацеплением Новикова могут при одних и тех же габаритных размерах г.ередавать в 1,5—2 раза большую мощность. Ввиду сложности изготовле- ния и монтажа передачи с зацеплением Новикова пока нашли применен: только в специальном машиностроении.

Шестерня Колесо

Рис. 3.20. Колесо с зацеплением М. Л. Новикова

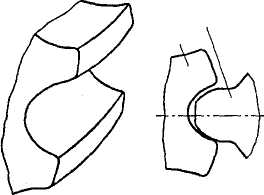
Рис. 3.21. Кинематика зацеп ния зубчатых колес

Какой профиль зуба получил наибольшее распространение в машиностроении?

3.19. Ответить на вопросы контрольной карточки 3.3.

Контрольная карточка 3.3

Вопрос	: Ответы	Ксл
Что называется полюсом зацепле­ния?	Точка касания двух соседних зубьев Отношение числа к к шагу зацепления Точка касания делительных (или начальных) ок­ружностей шестерни и колеса Точка касания линии зацепления с основной ок­ружностью шестерни или колеса	1 2 3 4
Покажите на рис. 3.22 активную линию зацепления (рабочий уча­сток)	Отрезок АД Отрезок ВС На чертеже не показан	5 6 7
Какой профиль имеют зубья пе­редачи, показанной на рис. 3.21?	Эльвовентный Циклоидальный Зацепление Новикова Эти профили в машиностроении не используются	8 9 10 11
Определить, сколько пар зубьев находится одновременно в зацеп­лении, если εa = 1,7	В течение 70 % времени в зацеплении находятся две пары, а в течение 30% времени — одна В течение 30 % времени в зацеплении находятся две пары, а в течение 70 % — одна	12 13
Какой угол зацепления принят для стандартных зубчатых колес, нарезанных без смещения	15 20 25 Любой	14 15 16 17

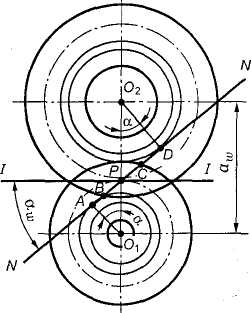
Рис. 3.22