§ 3. Основные элементы зубчатой передачи. Термины, определения и обозначения

3.12. Одноступенчатая зубчатая передача состоит из двух зубчатых ко­лес — ведущего и ведомого. Меньшее по числу зубьев из пары колес назы­вают шестерней, а большее колесом. Термин «зубчатое колесо» является об­щим. Параметрам шестерни (ведущего колеса) приписывают при обозначе­нии нечетные индексы (1, 3, 5 и т. д.), а параметрам ведомого колеса — четные (2, 4, 6 и т. д.).

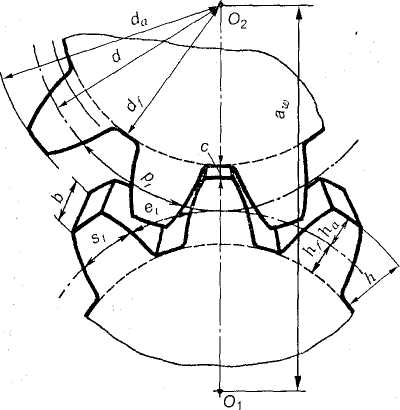
Зубчатое зацепление характеризуется следующими основными пара­метрами:

d_a — диаметр вершин зубьев;

d_r — диаметр впадин зубьев;

d_a — начальный диаметр;

d — делительный диаметр;

р — окружной шаг;

h — высота зуба;

h_a — высота ножки зуба;

с — радиальный зазор;

b — ширина венца (длина зуба);

е, — окружная ширина впадины зуба;

s, — окружная толщина зуба;

а_ш — межосевое расстояние;

а — делительное межосевое расстояние;

Z — число зубьев.

Делительная окружность — окружность, по которой обкатывается ин­струмент при нарезании. Делительная окружность связана с колесом и де­лит зуб на головку и ножку.

Основные элементы зубчатых колес представлены на рис. 3.15.

Рис. 3.15. Геометрические параметры цилиндрических зубчатых колес

Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.

Линейную величину, в п раз меньшую окружного шага зубьев, называют окружным модулем зубьев и обозначают т:

Размеры цилиндрических прямозубых колес вычисляют по окружному модулю, который называют расчетным модулем зубчатого колеса, или про­сто модулем; обозначают буквой т. Модуль измеряют в миллиметрах. Мо­дули стандартизованы (табл. 3.1).

Таблица 3.1. Стандартные значения модулей

1-й ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-й ряд
1	1,125	3	3,5	10	11	32	36
1,25	1,375	4	4,5	12	14	40	45
1,5	1,75	5	5,5	16	18	50	55
2	2,25	6	7	20	22	60	70
2,5	2,75	8.	9	25	28	80	90

Примечание. При назначении модулей первый ряд значений следует предпочитать второму.

Как условно делят зуб на две части — головку и ножку?

3.13. Ниже приведены определения остальных параметров зацепления.

Начальная окружность — каждая из взаимокасающихся окружностей зубчатых колес передачи, принадлежащая начальной поверхности данного зубчатого колеса.

Начальные окружности являются сопряженными, т. е. это понятие от­носится к паре колес, находящихся в зацеплении (к передаче). При измене­нии межосевого расстояния a_w начальные диаметры тоже соответственно изменяются, так как a_w равно сумме радиусов этих окружностей. Таким об­разом, у пары колес,; находящихся в зацеплении, может быть сколько угод­но начальных окружностей, в то время как для отдельно взятого зубчатого :<олеса понятие начальной окружности вообще лишено смысла.

По делительному диаметру d окружные шаги соответствуют стандарт­ному модулю т. Для цилиндрических прямозубых колес, например, p_t = тπ пли d= mz.

Для определения основных параметров зубчатой передачи принимают делительный радиус. Если межосевое расстояние в передаче равно сумме делительных радиусов, то начальные и делительные окружности в этом случае совпадают. В дальнейшем рассматривается именно такой частный случай зацепления.

Высота зуба h — радиальное расстояние между окружностями вершин и впадин зубчатого колеса:

h = h_a + h_f.

Головка зуба — его часть, расположенная между делительной окружно­стью цилиндрического зубчатого колеса и окружностью вершин зубьев; h — высота головки зуба.

Ножка зуба — часть зуба, расположенная между делительной окружно­стью и окружностью впадин (высота ножки зуба h_f).

Радиальный зазор — расстояние между поверхностями вершин зубьев и впадин шестерни и колеса:

c = h_f-h_a.

Окружная толщина зуба s, — расстояние между разноименными профи­лями зуба по дуге концентрической окружности зубчатого колеса.

Ширина венца b — наибольшее расстояние между торцами зубьев ци­линдрического зубчатого колеса по линии, параллельной его оси.

Межосевое расстояние а_ш — расстояние между осями зубчатых колес передачи.

Как определяется модуль зубьев? Могут ли иметь разный модуль шестер­ня и колесо в одной паре зубчатых колес? А у двух пар?

3.14. Ответить на вопросы контрольной карточки 3.2.

Контрольная карточка 3.2

Вопрос	Ответы	Код
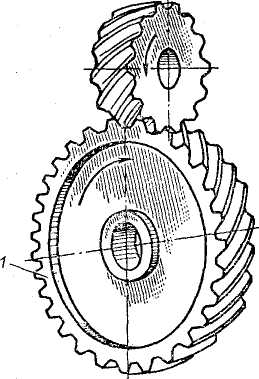
Как называется деталь, изображенная на рис. 3.16?	Зубчатое колесо цилиндрическое Зубчатое колесо коническое Червячное колесо	1 2 3
Как называется деталь 1, изображенная на рис. 3.17?	Червяк Шестерня Колесо зубчатое Звездочка Шкив	4 5 6 7 8
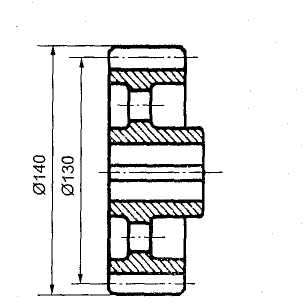
Как называется окружность (см. рис. 3.16), диаметр которой Ø 140 мм?	Начальная окружность Окружность вершин зубьев Делительная окружность Окружность впадин	9 10 11 12
Как называется окружность (см. рис. 3.16), диаметр которой Ø 130 мм?	Окружность ступицы колеса Окружность впадин Окружность вершин зубьев Делительная окружность	13 14 15 16
Напишите формулу для определения моду­ля зубчатого зацепления	π/рt р,/π hf-ha	17 18 19

Рис. 3.16 Рис. 3.17