5. Случайные величины

5.1. Основные понятия

Определение 5.1. Функция , определенная на множестве элементарных исходов , называется случайной величиной, если для каждого события вида , вероятность имеет смысл.

Определение 5.2. Законом распределения случайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всех возможных событий, связанных со случайной величиной.

Закон распределения случайной величины может быть задан, в частности, с помощью функции распределения.

Определение 5.3. Функция , определенная для всех , называется функцией распределения случайной величины Х.

Свойства функции распределения .

1. определена для всех .

2. для всех .

3. не убывает, то есть для любых .

4. , .

5. .

6. , где , то есть – непрерывная слева функция.

5.2. Дискретные случайные величины

Определение 5.4. Случайная величина Х называется дискретной, если множество ее возможных значений конечно или счетно.

Распределение дискретной случайной величины удобно описывать с помощью ряда распределения.

Определение 5.5. Рядом распределения (вероятностей) дискретной случайной величины Х называют таблицу (таблица 5.1), состоящую из двух строк: в первой строке перечислены все возможные значения случайной величины, а во второй – вероятности того, что случайная величина примет эти значения.

Таблица 5.1

			…
			…

Если число значений случайной величины счетное, то таблица содержит бесконечное множество ячеек. В таком случае должно быть задано правило, по которому определяются вероятности . Вероятности в этой таблице подчиняются условию (или соответственно в случае бесконечного множества элементарных исходов.)

Функция распределения дискретной случайной величины определяется как

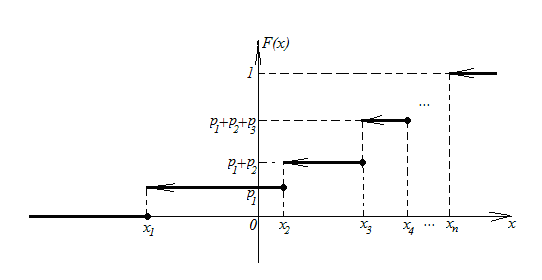
Функция распределения дискретной случайной величины является ступенчатой (рис. 7), причем величины скачков равны вероятностям соответствующих реализаций случайной величины .

рис. 7

Далее рассмотрим наиболее часто встречающиеся на практике распределения дискретных случайных величин.

1. Биномиальное распределение. Говорят, что дискретная случайная величина распределена по биномиальному закону, если она принимает значения с вероятностями

, ,

где , .

Заметим, что биномиальное распределение является распределением числа успехов в испытаниях по схеме Бернулли с вероятностью успеха .

2. Распределение Пуассона. Говорят, что дискретная случайная величина распределена по закону Пуассона, если она принимает целые неотрицательные значения с вероятностями

,

где – параметр распределения Пуассона.

Распределение Пуассона также называют законом редких событий, так как оно проявляется там, где производится большое число испытаний, в каждом из которых с малой вероятностью происходит «редкое» событие. В соответствии с законом Пуассона распределены, например, число вызовов, поступивших в течение суток на телефонную станцию; число метеоритов, упавших в определенном районе; число распавшихся частиц при радиоактивном распаде вещества.

3. Геометрическое распределение. Рассмотрим схему Бернулли. Пусть – число испытаний до первого «успеха». Тогда – дискретная случайная величина, принимающая значения с вероятностями

,

где .

В этом случае говорят, что дискретная случайная величина распределена согласно геометрическому закону.

Пример 5.1. Игральную кость бросают один раз. Если выпадает четное число очков, игрок выигрывает 8 у.е., если нечетное, но больше одного – проигрывает 1 у.е., если выпадает одно очко – проигрывает 10 у.е. Найти распределение случайной величины Х – величины выигрыша в данной игре.

Решение. Пространство элементарных исходов в данном случае имеет вид , где - выпадение i очков. .

Случайная величина Х может принимать три значения: , , , причем справедливо

, , .

Тогда

, , .

Ряд распределения случайной величины Х представлен в таблице 5.2.

Таблица 5.2

	-10	-1	8

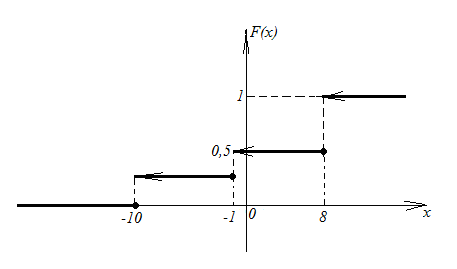
Найдем функцию распределения случайной величины Х. В силу определения получаем

Графическое изображение распределения случайной величины Х приведено на рис. 8.

рис. 8

Пример 5.2. Производят четыре независимых опыта, в каждом из которых некоторое событие А появляется с вероятностью . Построить ряд распределения случайной величины Х – числа появлений события А в четырех опытах.

Решение. В данной задаче реализуется схема Бернулли. Случайная величина Х распределена по биномиальному закону с параметрами , . Следовательно, закон распределения случайной величины Х примет вид:

.

Для получения ряда распределения вычислим соответствующие вероятности:

,

,

,

,

откуда

	0	1	2	3	4
	0,0016	0,0256	0,1536	0,4096	0,4096