Кириллов Исследование операций / Расчетно-графическое задание №3 по ИО вариант 4

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра экономической информатики

Расчетно-графическая работа

по дисциплине

«Исследование операций»

4 вариант

Факультет бизнеса

ФБИ – 22

Студенты:

Преподаватель:

Кириллов Ю.В.

Новосибирск 2014

Цели задания:

1. Понимать смысл, различать, осознанно использовать следующие понятия: математическая модель задачи целочисленного линейного программирования (ЗЦЛП); допустимая область решения ЗЦЛП; правильное отсечение в методе Гомори; релаксированная ЗЦЛП, разбиение множества решений релаксированной ЗЦЛП на подмножества, оценка подмножества решений, дерево решений, рекорд – в методе ветвей и границ для ЗЦЛП.

2. Получить навыки, уметь: строить математические модели ЗЦЛП; использовать различные методы для решения ЗЦЛП; анализировать полученное решение и находить альтернативные варианты при решении любым методом; интерпретировать полученные результаты в терминах решаемой задачи.

Условие задачи.

Коммерческая фирма закупила товары четырех видов по 10 упаковок каждого за пределами своего города. Доставку товаров предполагается осуществить собственным автофургоном грузоподъемностью V кг за несколько рейсов. Вес одной упаковки товара каждого вида равен соответственно v₁, v₂, v₃ и v₄ кг, а стоимость – c₁, c₂, c₃ и c₄ тысяч рублей.

Определить, какие виды товаров и в каком количестве необходимо перевезти первым рейсом, с тем, чтобы их стоимость была максимальной.

№ п/п	V	v1	v2	v3	v4	c1	c2	c3	c4
4	96	8	10	14	18	25	32	45	50

Математическая модель задачи:

Z(X) = 25x₁ + 32x₂ + 45x₃ + 50x₄ → max

8x₁+10x₂+14x₃+18x₄ ≤ 96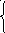

x₁ ,x₂ ,x₃ ,x₄ ≥ 0

Решение задачи методом Гомори:

Полагая, что свободные переменные равны 0, получим первый опорный план:

Таблица 1

Базис	x1	x2	x3	x4	x5	В
x5	8	10	14	18	1	96
∆(X0)	-25	-32	-45	-50	0

Таблица 2

Базис	x1	x2	x3	x4	x5	В
х4	8/18	10/18	14/18	1	1/18	96/18
∆(X0)	-50/18	-76/18	-110/18	0	50/18

Таблица 3

Базис	x1	x2	x3	x4	x5	В
х3	8/14	10/14	1	1	1/14	6
∆(X0)	5/7	1/7	0	110/14	45/14

8x1+10x2+4x4+x5>=12

-8x1-10x2-4x4-x5<=-12

Таблица 4

Базис	x1	x2	x3	x4	x5	х6	В
х3	8/14	10/14	1	1	1/14	0	6
х6	-8	-10	0	-4	-1	1	-12
∆(X0)	5/7	1/7	0	110/56	45/14	0

Вычисляем двойственные отношения (модуль отношения элементов ∆ - строки к соответствующим отрицательным элементам разрешающей строки). Наименьшее из этих отношений определяет разрешающий столбец. Для столбца Х1: ⁵/_56, для столбца Х2: ¹/_70, для столбца Х4: ¹¹⁰/_56, для столбца Х5: ⁴⁵/_14.

Выбираем столбец Х2 в качестве разрешающего:

Таблица 5

Базис	x1	x2	x3	x4	x5	Х6	В
х3	-16/14	0	1	1	0	1/14	6
х2	8/10	1	0	4/10	1/10	-1/10	12/10
∆(X0)	6/10	0	0	267/140	448/140	1/70

-8x₁-4x4-x₅+x₆ <= -12

Таблица 6

Базис	x1	x2	x3	x4	x5	Х6	X7	В
X3	-16/14	0	1	1	0	1/14	0	6
Х2	8/10	1	0	4/10	1/10	-1/10	0	12/10
X7	-8	0	0	-4	-1	1	1	-12
∆(X0)	6/10	0	0	267/140	448/140	1/70	0

Вычисляем двойственные отношения (модуль отношения элементов ∆ - строки к соответствующим отрицательным элементам разрешающей строки). Наименьшее из этих отношений определяет разрешающий столбец. Для столбца Х1: ⁶/_80, для столбца Х4: ²⁶⁷/_560, для столбца Х5: ⁴⁴⁸/_140.

Выбираем столбец Х1 в качестве разрешающего:

Таблица 7

Базис	x1	x2	x3	x4	x5	Х6	X7	В
X3	0	0	1	22/14	2/14	-1/14	-2/14	108/14
Х2	0	1	0	0	0	0	1/10	0
X1	1	0	0	4/8	1/8	-1/8	-1/8	12/8
∆(X0)	0	0	0	444/280	25/8	50/560	6/80

Т.к. max дробная часть в столбце В принадлежит строке Х₃, то она принимается за разрешающую.

-22х4-2х5+х6+2х7<= -10

Таблица 8

Базис	x1	x2	x3	x4	x5	Х6	X7	X8	В
X3	0	0	1	22/14	2/14	-1/14	-2/14	0	108/14
Х2	0	1	0	0	0	0	1/10	0	0
X1	1	0	0	4/8	1/8	-1/8	-1/8	0	12/8
X8	0	0	0	-22	-2	1	2	1	-10
∆(X0)	0	0	0	444/280	25/8	50/560	6/80	0

Для столбца Х4: ⁴⁴⁴/_6160, для столбца Х5: ²⁵/_16.

Выбираем столбец Х4 в качестве разрешающего:

Таблица 9

Базис	x1	x2	x3	x4	x5	Х6	X7	X8	В
X3	0	0	1	0	0	0	0	1/14	7
Х2	0	1	0	0	0	0	1/10	0	0
X1	1	0	0	0	14/176	-18/176	-14/176	4/176	224/176
X4	0	0	0	1	2/22	-1/22	-2/22	-1/22	10/22
∆(X0)	0	0	0	0	9181/3080	71/440	135/616	444/6160

Т.к. max дробная часть в столбце В принадлежит строке Х4, то она принимается за разрешающую.

-2х5+х6+2х7+х8<= -10

Таблица 10

Базис	x1	x2	x3	x4	x5	Х6	X7	X8	Х9	В
X3	0	0	1	0	0	0	0	1/14	0	7
Х2	0	1	0	0	0	0	1/10	0	0	0
X1	1	0	0	0	14/176	-18/176	-14/176	4/176	0	224/176
X4	0	0	0	1	2/22	-1/22	-2/22	-1/22	0	10/22
Х9	0	0	0	0	-2	1	2	1	1	-10
∆(X0)	0	0	0	0	9181/3080	71/440	135/616	444/6160	0

Для столбца Х5: ⁹¹⁸¹/_{6160 ,}

Выбираем столбец Х5 в качестве разрешающего:

Таблица 11

Базис	x1	x2	x3	x4	x5	Х6	X7	X8	Х9	В
X3	0	0	1	0	0					7
Х2	0	1	0	0	0					0
X1	1	0	0	0	0					154/176
X4	0	0	0	1	0					0
Х5	0	0	0	0	1					5
∆(X0)	0	0	0	0	0