Билет№6

1. Уравнение состояния идеального газа ( уравнение Менделеева – Клапейрона). Универсальная газовая постоянная. Изотермический процесс, изохорный процесс, изобарный процесс.

    Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти величины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.          Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона: pV = mRT/M, где р — давление, V — объем, m — масса, М — молярная масса, R — универсальная газовая постоянная. Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К (R = 8,31 ДжДмоль • К)).          Уравнение Менделеева—Клапейрона показывает, что возможно одновременное изменение трех параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два параметра. Особую роль в физике и технике играют три процесса: изотермический, изохорный и изобарный.          Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.          Изотермическим называют процесс, протекающий при постоянной температуре. Т = const. Он описывается законом Бойля—Мариотта: pV = const.          Изохорным называют процесс, протекающий при постоянном объеме. Для него справедлив закон Шарля: V = const, p/T = const.          Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид V/T = const прир = const и называется законом Гей-Люссака. 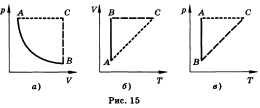Все процессы можно изобразить графически (рис. 15).          Реальные газы удовлетворяют уравнению состояния идеального газа при не слишком высоких давлениях (пока собственный объем молекул пренебрежительно мал по сравнению с объемом сосуда,                     в котором находится газ) и при не слишком низких температурах (пока потенциальной энергией межмолекулярного взаимодействия можно пренебречь по сравнению с кинетической энергией теплового движения молекул), т. е. для реального газа это уравнение и его следствия являются хорошим приближением.

2. Гармонические колебания. Амплитуда, период и частота колебаний маятника.

Механическими колебаниями называют движения тел, повторяющиеся точно или приблизительно одинаково через одинаковые промежутки времени. Силы, действующие между телами внутри рассматриваемой системы тел, называют внутренними силами. Силы, действующие на тела системы со стороны других тел, называют внешними силами. Свободными колебаниями называют колебания, возникшие под воздействием внутренних сил, например – маятник на нитке. Колебания под действиями внешних сил – вынужденные колебания, например – поршень в двигателе. Общим признаков всех видов колебаний является повторяемость процесса движения через определенный интервал времени. Гармоническими называются колебания, описываемые уравнением . В частности колебания, возникающие в системе с одной возвращающей силой, пропорциональной деформации, являются гармоническими. Минимальный интервал, через который происходит повторение движения тела, называется периодом колебаний Т. Физическая величина, обратная периоду колебаний и характеризующая количество колебаний в единицу времени, называется частотой . Частота измеряется в герцах, 1 Гц = 1 с^-1. Используется также понятие циклической частоты, определяющей число колебаний за 2 секунд . Модуль максимального смещения от положения равновесия называется амплитудой. Величина, стоящая под знаком косинуса – фаза колебаний, ₀ – начальная фаза колебаний. Производные также гармонически изменяются, причем , а полная механическая энергия при произвольном отклонении х (угол, координата, и т.д.) равна , где А и В – константы, определяемые параметрами системы. Продифференцировав это выражение и приняв во внимание отсутствие внешних сил, возможно записать, что , откуда .