4.3. Алгоритмы оценки качества окружающей среды с использованием доза-эффект зависимостей

4.3.1. Алгоритм анализа доза-эффект зависимостей для формирования лингвистического словаря оценок качества окружающей среды

Одним из важных этапов логико-вычислительных процедур принятия ре­шений по оценке и управлению качеством ОПС является этап лингвистическо­го (смыслового) представления результатов ранжирования или кластеризации показателей. На этом этапе ранжированные кластеры, полученные на преды­дущем этапе, приводятся к принятой системе лингвистических показателей, ха­рактеризующих качество экологического состояния ОПС и доступных для по­нимания и восприятия ЛПР. При этом следует различать две задачи:

- лингвистическое (смысловое) представление результатов кластеризации и ранжирования;

- пространственное районирование территории в районе промышленных производств в соответствии с лингвистическим представлением.

Понятие лингвистического (смыслового) представления связано с пробле­мой экологического зонирования территорий вокруг источников химического загрязнения природной среды, разработанной в Центре по проблемам экологии и продуктивности лесов РАН.

Экологическое зонирование можно осуществлять, пользуясь результатами анализа доза-эффект зависимостей, которые затем применяются при обработке космических изображений территории. Взаимосвязь доза - эффект позволяет получить объективные критерии для разграничения загрязненных ОПС на зоны экологического качества, что с учетом возможной взаимосвязи яркость изобра­жения - главная компонента МГК может быть использовано для выделения этих зон по космическому снимку.

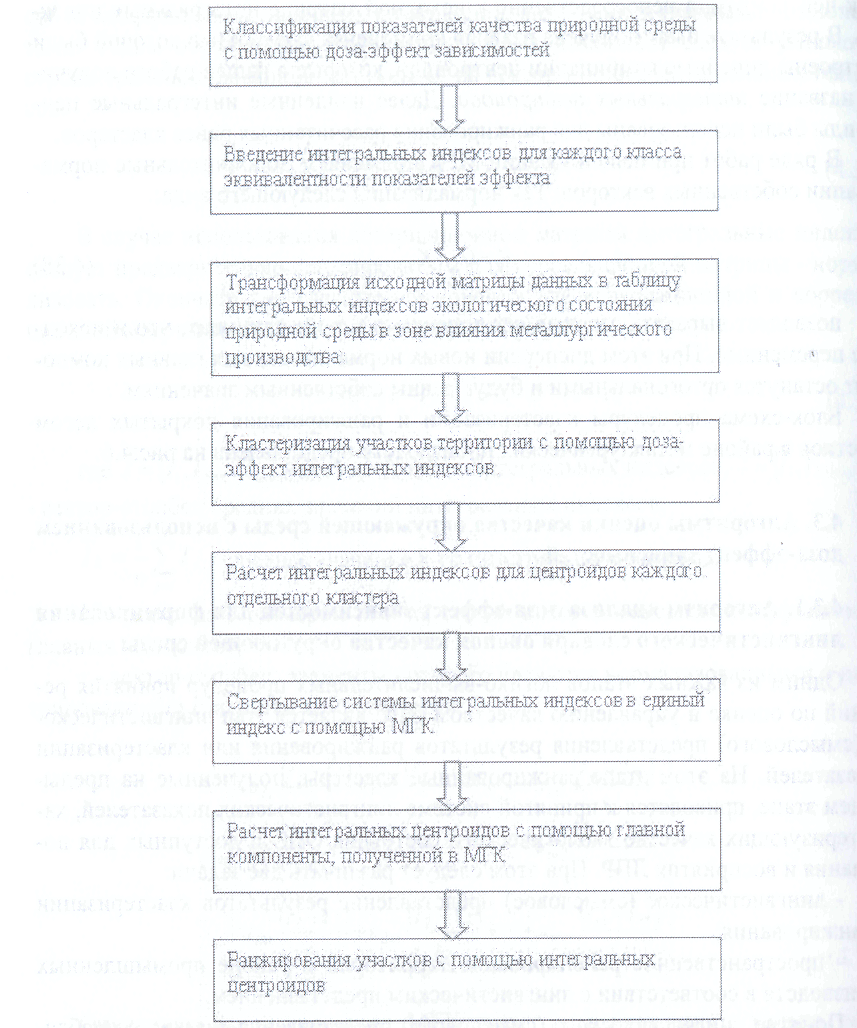
Рис.4.6. Блок-схема процедуры ранжирования участков покрытых ле­сом, расположенных в зоне влияния металлургического производства.

На рис.4.7 приведена экспериментальная зависимость доза-эффект в форме графика интегрального коэффициента сохранности (ИКС) для лесной террито­рии в районе металлургического комбината на Южном Урале.

Как следует из рис.4.7, в первом приближении доза-эффект зависимости можно представить с помощью логистической функции. Однако в ряде случаев такое упрощение не применимо. Так, например, для района металлургических производств могут быть получены графики доза-эффект зависимостей более сложного поведения.

Рис.4.7. Зависимость доза-эффект в форме графика интегрального коэффициента сохранности (ИКС) в %, вычисленного по шести фитоценометрическим показателям (запас древесины, масса хвои, жизненность доминантов, проективное покрытие, фитомасса и видо­вое разнообразие травяно-кустарничкового яруса, видовое разнооб­разие, мощность и запас подстилки) от суммарной нормализованной концентрации девяти основных загрязняющих токсикантов (S04, Мп, Cu,Zn,Cd,Pb,Fe,Co,Ni) в %

Рис.4.8. Доза - эффект зависимости: ИКС9 и ИКСВ9 в функции от суммарного загрязнения

Можно выделить четыре различных типа доза-эффект зависимостей, кото­рые приведены на рис.4.9. Поэтому вопрос о зонировании территории по доза-эффект зависимостям представляется гораздо более сложным. Если предполо­жить, что главную роль в эволюции лесных экосистем играют доза-эффект за­висимости логистического типа, то экологическое районирование можно про­водить, используя особенности логистической кривой.

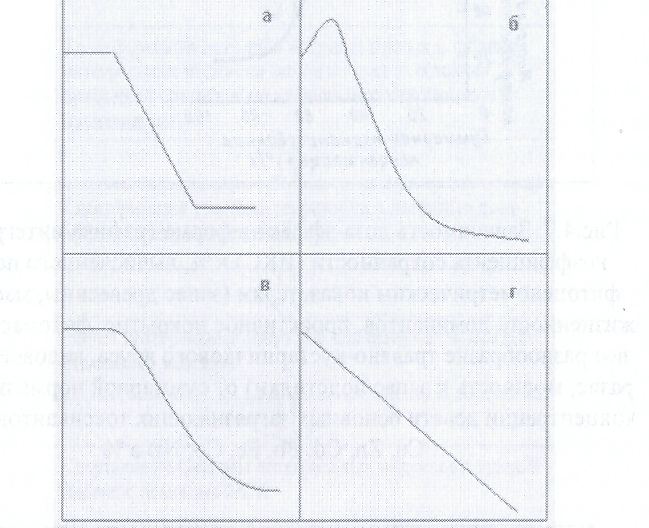
Рис.4.9. Различные типы доза-эффект зависимостей для лесных

экосистем: а - выраженные пороги токсического воздействия и полной

деградации; б - явление стимуляции вблизи порога токсического

воздействия; в - логистическая зависимость; г - отсутствуют пороги

токсического воздействия и полной деградации.

Обозначим эффект буквой - Y, а дозу буквой - X. Для выделения зон де­градации необходимо изучение зависимостей Y(X) доза - эффект. Нелинейная логистическая доза-эффект зависимость описывается функцией Ричардса. Для логистической зависимости, показанной на рис.4.7, функция Ричардса может быть представлена в следующем виде:

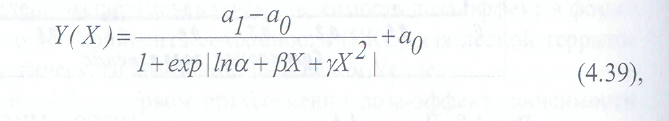
ские зоны: импактную, буферную и фоновую.

На рис.4.10 представлена теоретическая логистическая кривая (или логи­ста) построенная по формуле (4.39), а также ее производные первого, второго и тпетьего порядков, при следующих значениях параметров:

a=0, a₁=100, b=0.005, y=5

В уравнении (4.39) минимум первой производной dY/dX соответствует ко­ординате Хс = 0,32 - и отмечает центр зоны кризиса или зоны критических на­рушений (буферной зоны), а максимум второй производной diYldXi соответст­вует координате Х_р ~ 0,55 - центру буферной зоны. Третья производная имеет два экстремума: точка максимума Xf = 0,25 и точка минимума Х_,m„ = 0,75. Таким образом, дополнительное исследование функции Ричардса с помощью произ­водной третьего порядка выявляет две дополнительные критические точки на логистической кривой.

Все описанные выше особые точки могут быть использованы в качестве объективных критериев для экологического районирования территории и ран­жирования покрытых лесом участков в районе металлургических комбинатов.

Введем в соответствии с особыми точками графиков рис.4.10 следующие пять зон экологического районирования и соответствующие этим зонам лин­гвистические термы. Результаты представлены в табл.4.1.

Таким образом, могут быть получены объективные критерии, которые по­зволяют по критическим точкам логистической кривой "доза-эффект" выделять зоны деградации воздушно-загрязненных лесных экосистем. Точки экстрему­мов первой, второй и третьей производной от функции доза - эффект являются объективными критериями для выделения зон техногенной деградации лесов в районе металлургических комбинатов. Реально для практического районирова­ния территории могут быть использованы космические снимки. При этом необ­ходимо установление связи: космический снимок - интегральные индексы эффекта.

На рис.4.7 показана экспериментальная зависимость доза-эффект для тер­ритории в районе металлургического комбината на Южном Урале в форме за­висимости: эффект - интегральный коэффициент сохранности (ИКС), вычис­ленный по биогеоценометрическим показателям, и доза - суммарная нормали­зованная концентрация ингредиентов загрязнения. Уровень дозы определялся по содержанию токсикантов в снежном покрове. На рис.4.8 представлен график ИКС, вычисленный по девяти биогеоценометрическим показателям (запас дре­весины, масса хвои, жизненность доминантов, проективное покрытие, фито-масса и видовое разнообразие травяно-кустарничкового яруса, видовое разно­образие, мощность и запас подстилки) в функции суммарной нормализованной концентрации девяти основных загрязняющих токсикантов (SO₄, Mn, Cu, Zn, Cd, Pb, Fe, Co, Ni) в %. Экспериментальный максимум третей производной от­мечает первую критическую точку Х₁=22,342%, которая обозначает порог ток­сического воздействия и границу фоновой зоны. Минимум третей производной отмечает критическую точку при X₂=64,25%%, которая обозначает начало импактной зоны.

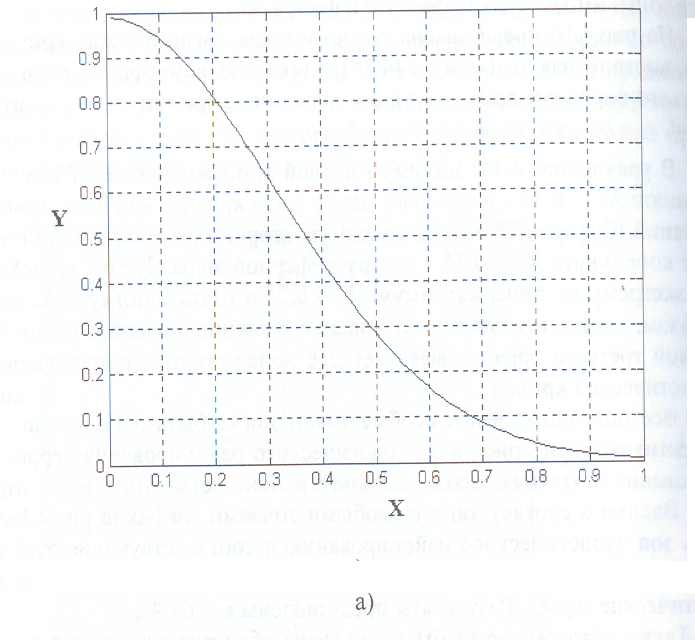
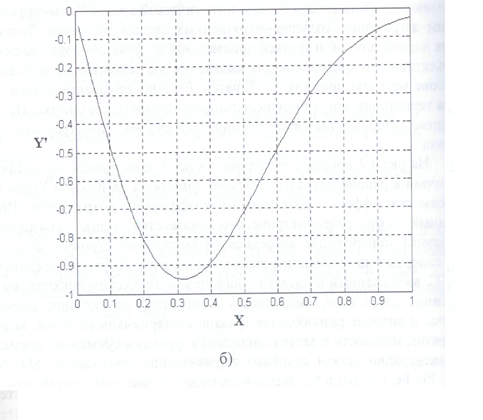
Рис.4.10. Теоретическая логистическая кривая, построенная по фор­муле (4.39) и ее производные первого и второго порядков: а - логистическая функция Ричардса, б, в и г - производные первого второго и третьего порядков функции Ричардса.

Введенные типовые лингвистические переменные, или термы образуют лингвистический словарь, который может быть использован для приписывания каждому из найденных и ранжированных кластеров определенного терма, соответствующего конкретной экологической зоне. Из рис.4.10,а следует, что имеется центральная зона, которая в нашей классификации (см. табл.4.1) полу­чила название буферной зоны. При делении термов на положительные и отри­цательные эта зона могла бы быть принята в качестве нейтрального терма. Од­нако в нашем алгоритме в качестве нейтрального терма принята вторая зона - зона риска. Центральная точка зоны риска - X_g = 0,29 разделят кластеры на две группы, которые нами были названы группами с положительной и отрицатель­ной экологией.

Рассмотрим случай, когда количество кластеров совпадает с количеством термов лингвистического словаря. Соответствующая блок-схема алгоритма экологического районирования представлена на рис.4.11.

В этом случае работа алгоритма идентификации (соответствия) кластеров термам лингвистического словаря должна начинаться с нахождения централь­ного кластера, центроид которого должен быть расположен предельно близко к центральной точке зоны риска - X_g = 0,29 в интервале:

Далее алгоритм идентификации, или соответствия разделяет все кластеры на две группы: с положительным и отрицательным состоянием ОПС. Кластеры с положительным состоянием ОПС расположены по дозе в диапазоне: 0 - 0,26, а кластеры с отрицательным состоянием ОПС в диапазоне 0,32 - 1.

Аналогичным образом термы лингвистического словаря также разделяют на две группы: {Фоновая зона} и {Буферная зона, Зона деградации, Импактная зона}.

Во второй группе кластеры получают имена термов в соответствии с результатами ранжирования.