4.2. Алгоритмы расчета многокритериальных и многоатрибутных по­казателей качества окружающей среды

4.2.1. Алгоритмы кластеризации лесных массивов

В предыдущем разделе описана методика получения таблиц интегральных индексов с нижними и верхними пределами (см. раздел 4.1). Каждый элемент таблицы представляет собой интегральный индекс в виде нечеткого симмет­ричного числа.

Для ранжирования и кластеризации земельных участков, покрытых лесом по экологическим показателям необходимо рассчитать показатели качества экосистемы соответствующего участка, выраженное в системе нечетких инте­гральных индексов. Дальнейшая кластеризация проводится в три этапа: для центров интегральных индексов, а также отдельно для нижней и верхней гра­ниц нечеткости интегральных индексов. В результате альтернативы (земельные участки) группировались в нечеткие кластеры (или классы). Известно, что классификация включает два основных метода: неконтролируемая классифика­ция без обучения (кластеризация) и контролируемая классификация с обучени­ем.

При неконтролируемой классификации объекты объединяются в отдель­ные кластеры, отличающиеся друг от друга по величине выбранных показате­лей. При наличии только двух показателей результат кластеризации может быть наглядно представлен на координатной плоскости. В настоящее время разработано достаточно большое количество алгоритмов кластеризации с ис­пользованием, как четких, так и нечетких методов обработки. Эти алгоритм¹"' можно разделить на три больших класса: эвристические, иерархические и разделительные. Последний класс наиболее часто используется для кластеризации изображений..

Кластерный анализ основан на понятиях плотности объектов, которая и кластера выше, чем вне его, на понятиях дисперсии, отделимости от их кластеров, формы (например, кластер может иметь очертания гиперсферы, гиперэллипсоида), размера и пр. Методы кластеризации делятся на агломеративные и дивизивные. В агломеративных, или объединительных методах ^Л исходит последовательное объединение наиболее близких объектов в один тер. процесс такого последовательного объединения можно представить физически _{в виде} дендрограммы, или дерева объединения. Это удобное представление позволяет наглядно изобразить процесс кластеризации, выполняемый агломеративными алгоритмами.

Исходными данными для анализа могут быть собственно объекты и их параметры, например, интегральные индексы, категория земель, состав насажде­ний возраст, диаметр, полнота, тип леса и др. В некоторых случаях данные для анализа удобно представлять матрицей расстояний между объектами, в которой на пересечении строки с номером i и столбца с номером о записано расстояние между 1-м и_)-м объектом. При отсутствии матрицы расстояний агломеративные алгоритмы начинают свою работу с вычисления расстояний между объектами. Расстояние между объектами в пространстве параметров является одной из многих мер сходства между объектами: чем меньше расстояние между объек­тами, тем они более схожи. При определении расстояний важную роль играет выбор метрики. Часто используют обычную евклидову метрику, например, ес­ли объект описывается двумя параметрами, то он может быть изображен точ­кой на фазовой плоскости, а расстояние между объектами — это расстояние между точками, вычисленное по теореме Пифагора. Если не возводить в квад­рат координаты вектора, а использовать их абсолютные значения то получится так называемое манхэттенское расстояние, или расстояние «городских кварта­лов».

Для некоторых задач евклидова метрика может оказаться вовсе неподхо­дящей. В этих задачах используется понятие меры сходства объектов (расстоя­ние - одна из возможных мер сходства). Важной мерой сходства, которая тра­диционно используется в статистике, является статистический коэффициент корреляции, например, коэффициент корреляции Пирсона.

Для бинарных данных используют другие меры сходства, например, вы­числяют количество параметров, которые совпадают у объектов, а затем полу­денный результат делят на общее число параметров и получают меру сходства. Такие меры называют коэффициентами ассоциативности. Из этих коэффициент наиболее популярны коэффициенты Жаккара и Гауэра.

При анализе результатов кластеризации необходимо учитывать особенно-использованных алгоритмов. В агломеративных методах применяются алгоритмы: одиночных связей, полных связей, средних связей и алгоритм Уорда. алгоритма Уорда состоит в том, чтобы проводить объединение, дающее минимальное приращение внутригрупповой дисперсии. Алгоритм Уорда при-^{т к} образованию кластеров примерно равных размеров и имеющих форму гиперсфер.

В некоторых алгоритмах кластеризации при отнесении объекта к очеред­ному кластеру используются интегральные характеристики кластеров. Приме­ром таких методов является итеративный алгоритм к-средних. В алгоритме к-средних вводится понятие центра кластера. Под расстоянием между объектом и кластером понимается расстояние между объектом и центром кластера. Клас­сифицируемый объект относится к тому кластеру, расстояние до которого ми­нимально. Обычно под расстоянием понимается евклидово расстояние, то есть объекты рассматриваются как точки евклидова пространства. Алгоритм к-средних состоит из следующих шагов:

1. Задается начальное разбиение данных на кластеры (число кластеров оп­ределяется пользователем). Затем вычисляются координаты центров кластеров.

2. Вычисляются расстояния от объектов до центров кластеров, в результа­те чего объекты перераспределяются по кластерам.

1. Вычисляются центры вновь образованных кластеров.

4) Шаги 2, 3 повторяются до тех пор, пока не будет найдена стабильная конфигурация, при которой кластеры перестанут изменяться, или число итера­ций не превысит заданное пользователем предельное значение.

Большую популярность в последнее время получили нечеткие алгоритмы, среди которых особенно широко известен алгоритм под названием «нечетких средних» - FСМА. Следует отметить, что главным недостатком алгоритмов к- и с-средних является необходимость априорного за­дания требуемого числа кластеров, а также других численных параметров, от величины которых существенно зависят результаты кластеризации. Из этого следует что, при использовании алгоритмов кластеризации необходимо иметь дополнительные критерии качества разделения объектов на кластеры, позво­ляющие численно оценить результат применения тех или иных параметров. Наиболее известные оценки качества кластеризации получили название коэф­фициентов кластеризации и энтропии.

Важной характеристикой алгоритма нечетких с-средних является то, что в результате его применения формируются нечеткие кластеры. При этом степень принадлежности объекта кластеру описывается с помощью функции принад­лежности. Рассмотрим сущность алгоритма нечетких с-средних. Пусть X = {х₁,х₂,...,х_п} заданная система из -векторов в пространстве признаков. При этом х_k^j - jя компонента к-го вектора, соответствующая j-му параметру. При нечеткой кластеризации не существует жесткого деления на классы, при кото­рой каждый вектор принадлежит только одному классу. Вместо этого вводятся степени принадлежности вектора каждому классу, которые называются функ­цией принадлежности (ФП): и_1к = и_к /,(x_k), где i= 1,с, с - число классов. Функция

принадлежности должна удовлетворять условию нормировки: ∑U_ik=1для всех k

Функция принадлежности заключает в себе гораздо больше полезной ин­формации, чем четкое разделение на классы. Так, например, при делении на три а объект, ФП которого примерно равна {1/3, 1/3, 1/3}, может рассматри-¹⁰¹ я как неподдающийся классификации и, соответственно, не принадлежа­щий ни одному из кластеров.

Целевая функция (ЦФ), используемая в алгоритме РСМА, имеет следую­щий вид:

(4.16)

где с! - расстояние в пространстве признаков между объектом к и центром

1-го кластера, т - параметр алгоритма.

Таким образом, ЦФ представляет собой сумму квадратов расстояний от всех объектов до центров кластеров, которая должна быть минимальной, т. е. ЦФ (4.16) является нечетким аналогом метода наименьших квадратов. Случай ш=0 соответствует алгоритму четкой кластеризации - жестких с-средних НСМА. Наилучшим решением задачи (4.16) является следующее:

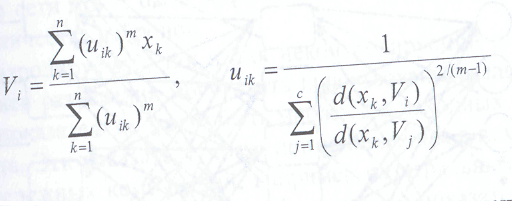
(4.17)

Из формул (4.17) следует, что центры кластеров рассчитываются, как средние арифметические, а функция принадлежности строится из отношений, показывающих на сколько объект к ближе к 1-му кластеру, чем к остальным.

Для расчета центров кластеров V_i по формулам (4.17) требуется предвари­тельно рассчитать функции принадлежности U_ik , которые в свою очередь тре­буют знания V_i;. Решение может быть найдено методом последовательных при­ближений.

К сожалению, алгоритмы нечетких средних (4.17) отсутствуют во многих популярных пакетах кластеризации и классификации.

Рассмотрим теперь преимущества и недостатки алгоритма контролируе­мой классификации (классификации с учителем). При контролируемой класси­фикации используются предварительно классифицированные опытным путем данные, которые составляют обучающую выборку. В результате обработки этих данных рассчитываются некоторые интегральные характеристики классов. Эти характеристики далее используются в процедуре классификации.

Подчеркнем, что успешность и эффективность алгоритма классификации с учителем в первую очередь определяется качеством и надежностью обучающей выборки, во-вторых - разделимостью используемых интегральных показателей ^и' в-третьих, эффективностью алгоритмов классификации. Так, например, в численных экспериментах, в случае использования плохо определенной обучающей выборки наблюдалась неудовлетворительная сходимость итерационно­го процесса обучения одного из мощнейших классификаторов - искусственной нейронной сети (ИНС).

В настоящее время ИНС все чаще используются для классификации и кла­стеризации объектов различного типа. Особенностью ИНС-алгоритмов являет­ся высокое требование, предъявляемое к быстродействию и оперативной памя­ти компьютеров в процессе обучения ИНС.

ИНС состоит из большого числа обрабатывающих элементов или нейро­нов, организованных в иерархические слои, в которых выходная переменная одного нейрона является входной переменной следующего нейрона. Нейрон­ные сети различаются способом соединения нейронов между собой и конструк­цией промежуточных слоев. Типичная нейронная сеть включает входной слой, промежуточные скрытые слои и выходной слой. Пример нейронной сети пока­зан на рис.4.

Рис.4.5. Блок-схема использованной для классификации искусствен­ной нейронной сети прямого распространения с алгоритмом обрат­ного распространения ошибки: Размер ИНС: 5x7 нейронов

Поясним работу ИНС на примере простейшей нейронной сети с к входны­ми нейронами, одним скрытым слоем с р нейронами и выходным слоем, со­стоящим из одного нейрона. Каждый нейрон скрытого слоя получает сигнал от нейронов входного слоя в следующем виде:I_j=∑ W_ij*, X_i, где i - номер узла входного слоя, j - номер узла скрытого слоя, X_i, - сигнал от i-го нейрона входно­го слоя, W_ij - весовые коэффициенты связи нейронов скрытого и входного сло­ев. Входной сигнал нейрона скрытого слоя I_j может быть преобразован в вы­ходной сигнал V_j при помощи различных нелинейных функций. Чаше других пользуется логистическое преобразование с монотонно возрастающим от нуля до единицы выходным сигналом следующего вида:

Выходной нейрон суммирует входные сигналы от нейронов скрытого слоя нормализует результат при помощи собственной передаточной функции. Обучающая выборка, включающая входные и известные результирующие вы­ходные данные, используется для настройки весовых коэффициентов сети, т.е. для обучения ИНС. При этом данные, полученные с выходного слоя, сравнива­ются с заранее известными результатами, и рассчитывается ошибка рассогласо­вания.

Эта ошибка передается по алгоритму нейронной сети в обратном направ­лении, что позволяет корректировать весовые коэффициенты в соответствии с используемым в данной ИНС алгоритмом минимизации. Эта процедура на­стройки весовых коэффициентов и называется обучением ИНС. Процесс обу­чения заканчивается либо при уменьшении ошибки рассогласования ниже за­данного порога, либо при выходе итерационного процесса на установившийся режим. В случае нечетких образов, характерных для космических изображений лесов, нейронные сети могут быть эффективны лишь при условии использова­ния большого количества нейронов.

Как для контролируемой, так и для неконтролируемой классификации в качестве критериев разделения могут быть использованы различные показате­ли. Исходными показателями могут быть множества исходных измеряемых по­казателей объекта. Эти показатели могут применяться как в исходном виде, так и в виде более сложных комбинаций, например интегральных индексов и пр. При применении контролируемой классификации эти показатели должны быть рассчитаны для каждого класса обучающей выборки. Таким образом, отклоне­ние характеристик объекта от интегральных характеристик кластера или класса может быть представлено в виде следующего много компонентного вектора, который назовем вектором рассогласования:

где аi^(k) - 1-я компонента к-о кластера, bi- характеристика объекта, n- ко­личество показателей, использованных для классификации.

Компоненты вектора рассогласования используются для построения раз­личных критериев и алгоритмов классификации. Самым простейшим и наибо­лее часто используемым на практике является линейная комбинация:

(4.19)

Где W_j - весовые коэффициенты, характеризующие приоритет соответствующего показателя. Линейные преобразования могут быть представлены в ви­де декомпозиции двух последовательных преобразований: подобия и поворота. Преобразование подобия изменяет длину радиуса-вектора объекта (в простран­стве признаков), а преобразование поворота - поворачивает радиус-вектор. При этом распознаваемый объект перемещается в пространстве признаков, удаляясь от одних кластеров и приближаясь к другим.

Аналогичный преобразователь используется при построении нелинейных ИНС:

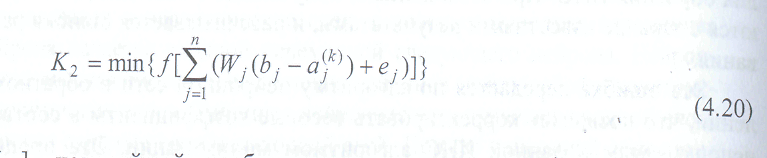
где f[...] - нелинейный преобразователь логистического (или ступенчатого) типа

Кроме простых рассогласований типа (4.18) в задачах классификации мо­гут быть использованы и более сложные комбинации.

Так вместо (4.18) хорошие результаты могут быть получены введением нормированных отклонений посредством деления абсолютных отклонений на стандартные отклонения соответствующих эталонов, т.е. с использованием не­линейных комбинаций показателей, в которых один из показателей будет нахо­диться в знаменателе.

В качестве критериев рассогласования часто применяют эвклидовы рас­стояния. В общем виде (с учетом весовых коэффициентов) критерий эвклидо­вых расстояний может быть представлен следующим образом:

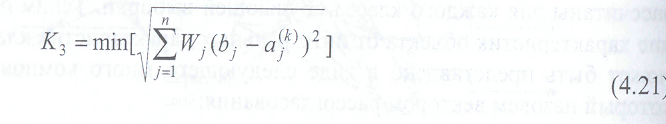
Этот критерий имеет наглядный геометрический смысл. Однако он может быть заменен любыми нелинейными преобразованиями, которые в ряде случаев являются более эффективными. К числу таких преобразований следует в пер­вую очередь отнести расстояния Минковского или расстояния городских квар­талов, а также преобразования по законам нормального или экспоненциального распределения.

Так, например, можно использовать критерий нормального распределения, который имеет следующий вид:

(4.22)

В случае необходимости получения иерархичной структуры кластеров применяются субтрактивные алгоритмы, например из пакета Матлаб. На начальном шаге работы алгоритма каждая запись базы данных (точка в пространстве параметров) принимается в качестве потенциального центра будущих кластеров. Далее при помощи выбранной потенциальной функции определяется точка с наибольшим потенциалом, которая принимается центр кластера. Важными параметрами алгоритма кластеризации, которые играют ведущую роль при кластеризации, являются радиусы кластера, которые задаются по каждому параметру отдельно. Все точки, расположенные вблизи выбранного центра кластера на расстоянии меньшем радиуса, не могут быть центрами других кластеров. Среди остальных точек вновь определяется точка с наибольшим потенциалом, которая и становиться центром второго кластера. Эта процедура повторяется до тех пор, пока не будут исчерпаны все точки базы

данных.

Потенциал точки рассчитывается по следующей формуле:

где Р_j - потенциал j-й точки, x_k^(p) - р-я координата k- й точки, г^(p) - радиус

кластера вдоль р-й координаты.

Центром кластера становится точка с наибольшим значением Р_j. Кроме ра­диусов в алгоритме вводятся еще три параметра:

Squash -фактор - коэффициент, на который умножаются радиусы, для того чтобы в случае необходимости подобным образом изменять размеры кластеров, не меняя при этом исходных пропорций между ними.

Ассерt-фактор - устанавливает верхнюю границу в долях исходного потен­циала, только выше которой другая точка может стать центром нового класте­ра.

Реjесг-фактор - устанавливает нижнюю границу в долях исходного потен­циала, ниже которой другая точка не может стать центром нового кластера.

В программе Матлаб, реализующей алгоритм, имеется вспомо­гательное окно, в котором могут быть представлены двухмерные сечения мно­гомерных данных. Кроме того возможно использование не только алгоритма Sиbtrасtivе, но и алгоритма FСМА. В качестве X и Y координат двухмерных се­чений могут быть заданы любые показатели качества природной среды.

В настоящее время особенно популярным является использование для це­лей кластеризации самоорганизующихся ИНС. Эти сети были разработаны Центром исследований искусственных нейронных сетей и Лабораторией ин­формационных и компьютерных исследований Технологического университета города Хельсенки (Финляндия) и получили название самоорганизующихся нейронных сетей Кохонена. На сайте: www.cis.hut.fi/research имеется пакет прикладных программ самоорганизующихся сетей (SОМ – Seft organizing mар), предоставленный Центром исследований ИНС для свободного пользования. Кроме того, в пакете Матлаб имеется достаточно хорошо зарекомендовавшая с ебя реализация данного алгоритма.

В своей простейшей форме сеть Кохонена функционирует по правилу «по­бедитель получает все». Для данного входного вектора один и только один ней­рон Кохонена выдает логическую единицу, все остальные выдают ноль. Выход каждого нейрона Кохонена является просто суммой взвешенных элементов входных сигналов:

где Sj — выход j-ro нейрона Кохонена; Wj = (w_1j, w_2j,... w_nj) - вектор весов j-го нейрона Кохонена; X = (x_1i,X_2i,.., х„) - вектор входного сигнала, или в вектор-но-матричной форме:

где S — вектор выходов слоя Кохонена.

Нейрон Кохонена с максимальным значением Sj является «победителем». Его выход равен единице, у остальных нейронов он равен нулю.

Обучение слоя Кохонена осуществляется следующим образом. Слой Ко­хонена классифицирует входные векторы в группы схожих векторов. Это дос­тигается с помощью такой подстройки весов, что близкие входные векторы ак­тивизируют один и тот же нейрон данного слоя.

Слой Кохонена обучается без учителя (самообучается). В результате уче­ния слой приобретает способность разделять несхожие входные векторы. Какой именно нейрон будет активизироваться при предъявлении конкретного входно­го сигнала, заранее трудно предсказать.

При обучении слоя Кохонена на вход- подается входной вектор, и вычис­ляются его скалярные произведения с векторами весов всех нейронов. Скаляр­ное произведение является мерой сходства между входным вектором и векто­ром весов. Нейрон с максимальным значением скалярного произведения объяв­ляется «победителем», и его веса подстраиваются (весовой вектор приближает­ся к входному). Уравнение, описывающее процесс обучения, имеет вид:

где w_n - новое значение веса, соединяющего входной компонент х с выиг­равшим нейроном, w_s - предыдущее значение этого веса,n - коэффициент ско­рости обучения.

Каждый вес, связанный с выигравшим нейроном Кохонена, изменяется пропорционально разности между его величиной и величиной входа, к которо­му он присоединен. Направление изменения минимизирует разность между ве­сом и соответствующим элементом входного сигнала.

Коэффициент скорости обучения n вначале обычно полагается равным 0,7 и может затем постепенно уменьшаться в процессе обучения. Это позволяет делать большие начальные шаги для быстрого грубого обучения и меньшие шаги _при подходе к окончательной величине.

Если бы с каждым нейроном Кохонена ассоциировался один входной век­тор, то слой Кохонена мог бы быть обучен с помощью одной коррекции на вес (n = 1)- Как правило, обучающее множество включает много сходных между собой входных векторов, и сеть должна быть обучена активизировать один и тот же нейрон Кохонена для каждого из них. Веса этого нейрона должны полу­чаться усреднением входных векторов, которые должны его активизировать.

При необходимости включения в число критериев качества ОПС (инте­гральных индексов) дополнительных экспертных оценок следует использовать манхэттенскую метрику, так как при сравнении двух лингвистических оценок обычно используют их численные аналоги, что лучше соответствует манхэттенской метрике.

Главным результатом на данном этапе является редукция разнородных данных по доза-эффект зависимостям в систему однородных комплексных ин­тегральных оценок качества ОПС, которые намного надежнее при их использо­вании для целей кластеризации.

Следует отметить, что, несмотря на важное значение, которое имеет про­цедура кластеризации, т.е. разделения покрытых лесом участков на отдельные кластеры, большой интерес представляет изучение и анализ дерева классов (дендрограммы). Дендрограмма позволяет исследовать степень подобия участ­ков, попадающих в различные соседние кластеры. Информация о подкластерах данного кластера позволяет вводить дополнительную дифференциацию участ­ков внутри кластера. С другой стороны вхождение конкретного кластера в кла­стеры более высокого уровня позволяют оценить сходство между отдельными кластерами.