- •Порядок выполнения измерений
- •Обработка результатов измерений
- •Принцип Гюйгенса-Френеля
- •Дифракция Френеля и Фраунгофера
- •Лабораторная работа №3.6 изучение явления дифракции фраунгофера от одной щели
- •1. Описание установки
- •2. Порядок выполнения измерений
- •3. Обработка результатов измерений
- •Лабораторная работа №3.7 изучение прозрачной дифракционной решетки
- •1. Описание установки
- •2. Порядок проведения измерений
- •Обработка результатов измерений
- •Контрольные вопросы
- •Изучение плоскополяризованного света Общие сведения
- •Лабораторная работа № 3.8 изучение плоскополяризованного света
- •1. Описание установки
- •2. Порядок выполнения измерений
- •3. Обработка результатов измерений
- •Заключение
- •Контрольные вопросы
- •Список рекомендуемой литературы
- •Структура отчета
- •Требования к содержанию разделов отчета
- •1. Описание установки
- •2. Порядок выполнения измерений
- •3. Обработка результатов измерений
- •Правила оформления отчета
- •1. Общие требования
- •2. Нумерация разделов, подразделов, пунктов
- •3. Иллюстрации
- •4. Формулы и уравнения
- •5. Таблицы
- •Министерство образования и науки российской федерации Федеральное государственное бюджетное образовательное учреждение «ковровская государственная технологическая академия имени в.А. Дегтярева»
2. Порядок проведения измерений
2.1. Включить ртутную лампу и освещение шкалы гониометра. Проверить резкость изображения центрального максимума и визира в поле зрения окуляра 5.
2.2. Измерить угол для центрального максимума.
2.3. Измерить углы дифракции для фиолетовой, зеленой и двух желтых линий спектра с обеих сторон от центрального максимума.
2.4. Повторить измерения согласно заданию преподавателя.
2.5. Измерить при помощи штангенциркуля ширину световой полосы h, падающей на дифракционную решетку.
2.6. Результаты измерений занести в самостоятельно разработанную таблицу.
Обработка результатов измерений
3.1. Считая длину волны зеленой спектральной линии ртути в качестве эталонной λ=546,073 нм, определить период дифракционной решетки по формуле (2).
3.2. Зная период дифракционной решетки, определить по формуле (2) неизвестные длины волн спектральных линий ртути.
3.3. Оценить погрешность измерений периода дифракционной решетки и неизвестных длин волн спектральных линий ртутной лампы. Анализ погрешностей выполнить согласно методическим указаниям [5].
3.4. С помощью координатной оси сравнить рассчитанные длины волн с их теоретическими значениями.
3.5. Рассчитать
угловую дисперсию D1
по
формуле
 для всех длин волн.
для всех длин волн.
3.6. По
результатам измерений определить
значение
угловой дисперсии D2 = 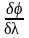 для
желтых линий
ртутной лампы. Сравнить полученное
значение угловой дисперсии с D1
по формуле:
для
желтых линий
ртутной лампы. Сравнить полученное
значение угловой дисперсии с D1
по формуле:
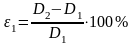 .
.
3.7. Рассчитать
разрешающую способность дифракционной
решетки R1
по формуле
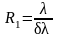 для
желтых линий спектра ртутной
лампы.
для
желтых линий спектра ртутной
лампы.
3.8. Определить
число действующих штрихов решетки
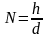 .
Определить значение разрешающей
способности R2 = mN.
Сравнить полученное значение разрешающей
способности с
R1
по формуле:
.
Определить значение разрешающей
способности R2 = mN.
Сравнить полученное значение разрешающей
способности с
R1
по формуле:
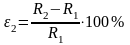 .
.
3.9. Сделать вывод о проделанной работе. Указать все полученные физические величины в виде: xист.=х±Δх, ε (ответ округлить по правилам).
Контрольные вопросы
1. Дайте определение дифракции.
2. Объясните принцип действия дифракционной решетки.
3. Объясните принцип действия гониометра.
4. Чем различаются дифракция монохроматического и белого света?
5. Дать определения основным характеристикам дифракционной решетки.
6. Сформулировать критерий Рэлея.
Изучение плоскополяризованного света Общие сведения
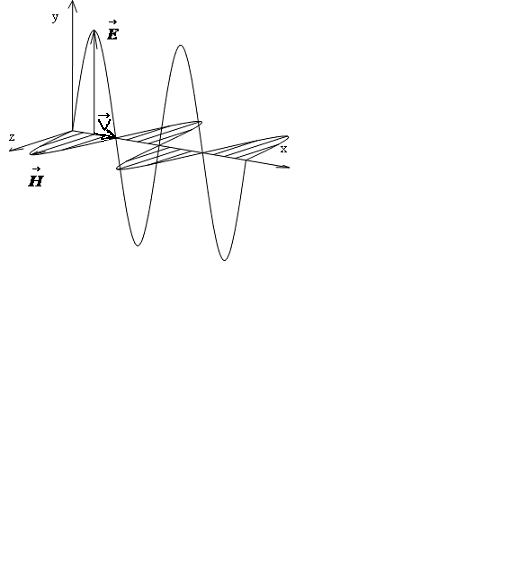
Волновая теория описывает свет, как распространяющиеся в пространстве колебания электромагнитного поля (рис.1). Векторы напряженности электрического и магнитного полей располагаются в плоскости, перпендикулярной направлению распространения волны, то есть эти волны являются поперечными. Явление поляризации связано с поперечными волнами.
Рис.1. Электромагнитная волна |
В
дальнейшем будем указывать положение
только одного вектора
|
Свет, в котором направление колебаний светового вектора меняется с течением времени непредсказуемо, называется естественным. Такой свет излучают все естественные источники света. Свет, в котором направление колебаний вектора со временем не изменяется, называется плоскополяризованным, т.е. колебания вектора происходят только в одной проходящей через луч плоскости. Плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой волны, называется плоскостью поляризации. Свет называется эллиптически поляризованным, если вектор поворачивается вокруг луча и одновременно изменяется по величине, в результате чего конец вектора описывает эллипс. Если конец вектора описывает окружность, то свет называется поляризованным по кругу.
Поляризация света происходит при отражении света от поверхности диэлектриков, при преломлении в них, а также при прохождении света через анизотропные среды, например, через кристаллы кварца, турмалина, исландского шпата и т.д., если направление луча света не совпадает с оптической осью кристалла. Если в отраженном луче колебания, перпендикулярные к плоскости падения, преобладают над колебаниями других направлений, то такой луч будет частично поляризован.
Приборы, предназначенные для получения поляризованного света, называются поляризаторами. На глаз поляризованный свет нельзя отличить от естественного. Приборы, предназначенные для исследования (анализа) поляризованного света, называются анализаторами. Один и тот же прибор можно использовать либо как поляризатор, либо как анализатор.
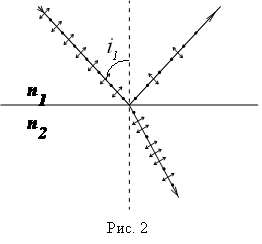
Луч естественного света, падающий на границу раздела двух сред (рис.2), в общем случае можно представить совокупностью двух плоскополяризованных лучей, поляризация которых произошла в двух взаимно перпендикулярных направлениях. Будем считать, что в одной части падающего света вектор колеблется перпендикулярно плоскости чертежа. Эти направления колебаний вектора изображаются точками (рис. 2). В другой части падающего света вектор колеблется в плоскости чертежа. Эти направления колебаний вектора изображаются двухсторонними стрелками (рис.2).
Рис.2. Поляризация на границе раздела двух сред |
Поскольку все направления в естественном луче равноценны, то на каждое из двух выбранных направлений колебаний вектора приходится половина интенсивности падающего света. Отражение света с различной ориентацией вектора относительно плоскости раздела двух сред |
п роисходит
по-разному.
В отраженном луче интенсивность света
с колебаниями вектора
,
перпендикулярном плоскости чертежа,
будет больше, чем интенсивность света
с колебаниями вектора
в плоскости чертежа. Соответственно, в
прошедшем луче интенсивность последних
колебаний (в плоскости чертежа) будет
больше, а первых – меньше; оба луча
оказываются частично поляризованными.
роисходит
по-разному.
В отраженном луче интенсивность света
с колебаниями вектора
,
перпендикулярном плоскости чертежа,
будет больше, чем интенсивность света
с колебаниями вектора
в плоскости чертежа. Соответственно, в
прошедшем луче интенсивность последних
колебаний (в плоскости чертежа) будет
больше, а первых – меньше; оба луча
оказываются частично поляризованными.
Степень
поляризации отраженного луча меняется
при изменении угла падения
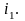 Существует
угол падения, при котором отраженный
луч оказывается полностью поляризованным.
Он называется углом полной поляризации
или углом
Брюстера
(tgib
или tgin
на рис.3). Если угол падения равен углу
Брюстера, то отраженный и преломленный
лучи взаимно перпендикулярны.
Существует
угол падения, при котором отраженный
луч оказывается полностью поляризованным.
Он называется углом полной поляризации
или углом
Брюстера
(tgib
или tgin
на рис.3). Если угол падения равен углу
Брюстера, то отраженный и преломленный
лучи взаимно перпендикулярны.
Тангенс угла полной поляризации равен относительному показателю преломления второй среды относительно первой:
tg ib= n21. (1)
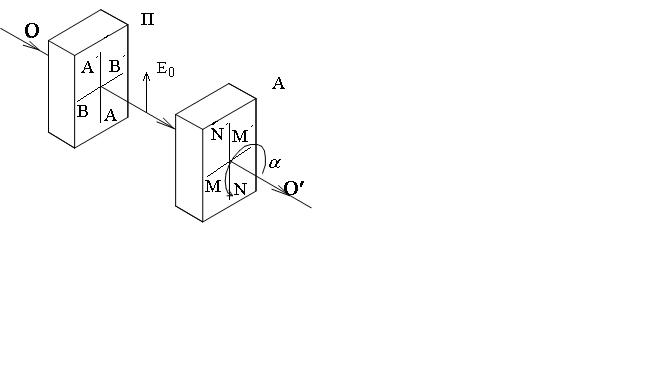
Поляроидами называются вещества, обладающие способностью поляризовать проходящий через них естественный свет. Поляроидами могут служить пластинки, вырезанные из кристалла турмалина, или целлулоидные пленки, покрытые тонким слоем мелких кристаллов герапатита. Интенсивность света, прошедшего обе пластинки, зависит от их взаимной ориентации: при некотором положении пластинок она оказывается наибольшей, а затем при вращении пластинки А (анализатора) интенсивность прошедшего света уменьшается до нуля (рис.4).
Рис.4. Поляризация света поляроидами |
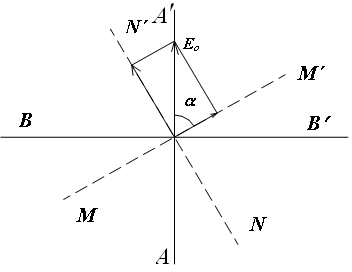
Рис. 5. Колебания вектора
|
Э Пусть кристалл П пропускает волны,
световой вектор которых колеблется в
плоскости
Пусть кристалл П пропускает волны,
световой вектор которых колеблется в
плоскости
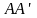 (рис.5), являющейся главной плоскостью
пластинки. Каждый вектор
,
колеблющийся в некотором другом
направлении, можно разложить на два
взаимно перпендикулярных вектора,
колебания которых будут совершаться
вдоль направлений
и
(рис.5), являющейся главной плоскостью
пластинки. Каждый вектор
,
колеблющийся в некотором другом
направлении, можно разложить на два
взаимно перпендикулярных вектора,
колебания которых будут совершаться
вдоль направлений
и
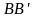 .
Следовательно, естественный свет можно
представить совокупностью двух
поляризованных лучей, в одном из которых
вектор
колеблется в направлении
.
Пластинка П,
задерживая половину интенсивности
света, отвечающую колебаниям вектора
в направлении
(горизонтальной плоскости), превращает
естественный свет в плоскополяризованный.
.
Следовательно, естественный свет можно
представить совокупностью двух
поляризованных лучей, в одном из которых
вектор
колеблется в направлении
.
Пластинка П,
задерживая половину интенсивности
света, отвечающую колебаниям вектора
в направлении
(горизонтальной плоскости), превращает
естественный свет в плоскополяризованный.
На
пластинку А
падает уже поляризованный свет. В
зависимости от ориентации пластинки А
из этого
поляризованного света пропускается
большая или меньшая часть. Пусть пластинка
А
ориентирована таким образом, что
пропускает свет с колебаниями вектора
в направлении плоскости
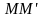 ,
являющейся главной плоскостью пластинки
А и составляющей угол
с главной плоскостью пластинки П
(направлением
,
являющейся главной плоскостью пластинки
А и составляющей угол
с главной плоскостью пластинки П
(направлением
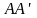 ,
рис. 5). Вектор
в падающем на луче колеблется вдоль
направления
(рис. 5). Амплитуду колебаний вектора
в падающем на пластинку А
луче обозначим
,
рис. 5). Вектор
в падающем на луче колеблется вдоль
направления
(рис. 5). Амплитуду колебаний вектора
в падающем на пластинку А
луче обозначим
 .
Колебания вектора
вдоль
могут быть разложены на составляющие
колебания:
.
Колебания вектора
вдоль
могут быть разложены на составляющие
колебания:
вдоль с амплитудой:
с амплитудой:
 ;
(2)
;
(2)
и
вдоль
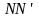 с амплитудой:
с амплитудой:
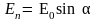 .
(3)
.
(3)
Пластинка
А пропустит
колебания с амплитудой
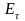 и полностью погасит колебания с амплитудой
и полностью погасит колебания с амплитудой
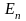 .
Согласно волновой теории, интенсивность
световых волн пропорциональна квадрату
амплитуды
колебаний вектора
в волне. Вследствие этого можно записать:
.
Согласно волновой теории, интенсивность
световых волн пропорциональна квадрату
амплитуды
колебаний вектора
в волне. Вследствие этого можно записать:
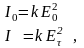 (4)
(4)
где k – некоторый коэффициент пропорциональности, а I0 и I – интенсивности поляризованного света, падающего на пластинку А и вышедшего из нее.
Возводя выражение (2) в квадрат и решая его совместно с формулами (4), приходим к выводу:
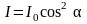 .
(5)
.
(5)
Отсюда
следует, что интенсивность вышедшего
луча I
пропорциональна
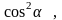 где
– угол между плоскостью колебаний
падающего света и главной плоскостью
поляризатора. Интенсивность оказывается
наибольшей, когда
= 0
и равной
нулю (свет задерживается полностью),
когда главные плоскости пластинок
перпендикулярны, и интенсивность имеет
промежуточное значение при промежуточных
положениях пластинок. Выражение (5)
представляет собой закон
Малюса для
полностью поляризованного света. Для
частично поляризованного света:
где
– угол между плоскостью колебаний
падающего света и главной плоскостью
поляризатора. Интенсивность оказывается
наибольшей, когда
= 0
и равной
нулю (свет задерживается полностью),
когда главные плоскости пластинок
перпендикулярны, и интенсивность имеет
промежуточное значение при промежуточных
положениях пластинок. Выражение (5)
представляет собой закон
Малюса для
полностью поляризованного света. Для
частично поляризованного света:
I = Imin +(Imax – Imin)cos2. (6)
Степенью поляризации называется величина:
Р = (Imax – Imin)/(Imax + Imin). (7)
В этих выражениях Imax и Imin – максимальная и минимальная интенсивности света, соответствующие двум взаимно перпендикулярным компонентам светового вектора.

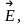 так как вектор
так как вектор
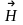 однозначно связан с ним. Вектор
однозначно связан с ним. Вектор
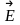 называют также световым вектором, ибо
именно он определяет взаимодействие
света с веществом, встречающемся на
его пути.
называют также световым вектором, ибо
именно он определяет взаимодействие
света с веществом, встречающемся на
его пути.