3. Обработка результатов измерений

3.1. Учитывая темновой ток, провести расчет фототока по результатам таблицы 1 и построить график распределения интенсивности в дифракционной картине I = f(x), считая интенсивность пропорциональной фототоку. При вычислениях фототока учитывайте положение множителя микроамперметра.

3.2. На том же графике отметить координаты максимумов и минимумов интенсивности (рис.3), рассчитывая максимумы х по формуле (10) при m=±1, ±2,…,а минимумы х по формуле (9). При расчетах необходимо учесть, что для малых углов: sinφ ≈ tgφ = х/l . Для расчета интенсивности боковых максимумов: I₁=I₀*0,045; I₂=I₀*0,016; I₃=I₀*0,008. Длина волны гелий – неонового лазера: λ =632,8 нм.

3.3. Рассчитать погрешности интенсивности боковых максимумов, а также погрешности максимальных и минимальных значений х по отклонениям экспериментальных точек от теоретической кривой:

*100%.

3.4. По данным, занесенным в заданную таблицу (по указанию преподавателя), исходя из формулы (9) для расчета минимумов интенсивности и, учитывая, что для малых углов sinφ ≈ tgφ = х/l, вычислить экспериментальную длину волны гелий-неонового лазера по первому минимуму. Значение первого минимума задавать как среднее арифметическое значений х₊ и х_-.

3.5. Найти среднее значение и доверительный интервал длины волны как результат прямых многократных измерений [5] и сравнить ее с истинной.

Заключение

Сделать вывод о проделанной работе. Указать все полученные физические величины в виде: x_ист. = х±Δх, ε (ответ округлить по правилам).

Контрольные вопросы

1. Что называется дифракцией света?

2. Объясните принцип Гюйгенса – Френеля.

3. Чем отличается дифракция Фраунгофера от дифракции Френеля?

4. В чем заключается метод зон Френеля?

5. Опишите явление дифракции Фраунгофера на узкой щели. Запишите условия максимумов и минимумов.

6. Что представляет собой график распределения интенсивности на экране от одной щели?

ДИФРАКЦИЯ НА ПРОЗРАЧНОЙ

ДИФРАКЦИОННОЙ РЕШЕТКЕ

Общие сведения

Дифракцией называется совокупность явлений, наблюдаемых при распространении световых волн в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Наиболее интересный случай дифракции наблюдается при использовании дифракционной решетки.

Плоская прозрачная дифракционная решетка (рис. 1) представляет собой прозрачную пластину с большим количеством (до нескольких тысяч на 1 мм) тонких параллельных щелей одинаковой ширины b и равными расстояниями d между их серединами (или соответствующими точками). Щели решетки образуют правильную структуру. Так как такая структура имеет различный коэффициент пропускания света через щели и промежутки между ними, то решетка такого типа называется прозрачной амплитудной решеткой. Расстояние d называется периодом или постоянной решетки.

Рис. 1. Дифракция Фраунгофера на дифракционной решетке

Распределение интенсивности в дифракционной картине получим, если учтем распределение интенсивностей от дифракции от каждой щели, а также взаимную интерференцию волн от всех щелей. Так как колебания, приходящие от различных щелей, являются когерентными, то для нахождения результирующей интенсивности при их наложении необходимо найти фазовые соотношения между ними. Для этого разобьем открываемую часть волновой поверхности на очень узкие зоны, параллельные щелям. Вектор амплитуды колебаний, создаваемый i-й зоной в точке Р, обозначим А_i. Тогда вектор результирующих колебаний можно представить в таком виде:

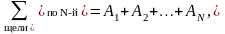
где А_i – вектор колебаний, создаваемый i-й щелью в точке Р.

Модули всех этих векторов одинаковы для каждого угла дифракции , но зависят от угла дифракции при его изменении. Световые лучи от отдельных щелей будут интерферировать в соответствии с принципом интерференции: если в разности хода интерферирующих лучей укладывается целое число длин волн, результатом интерференции будет максимум интенсивности. Для углов дифракции при выполнении этого условия амплитуда колебаний от отдельных щелей складывается:

А = ΣА_i = NА_i = max.

Такие максимумы называются главными. Интенсивность главных максимумов I_max пропорциональна квадрату числа щелей решетки:

I_max= N²I_φ,

где I_φ – интенсивность, создаваемая одной щелью в направлении .

Условием возникновения максимумов, называемых главными, будет:

Δ = d·sin φ_m = ± mλ, (m = 0,1,2,3…). (1)

Между главными максимумами при интерференции световых лучей возникают максимумы малой интенсивности, называемые дополнительными. Механизм и условия их возникновения проанализируем на примере интерференции световых волн от пяти щелей (рисунок 2).

Рис. 2. Дифракция Фраунгофера от пяти щелей

При φ = 0 разность хода световых лучей от отдельных щелей:

Δ₅ = Δ₄ = Δ₃ = Δ₂ = Δ₁ = 0, А₅ + А₄ + А₃ + А₂ + А₁ = NА₁.

Возникает центральный (главный) максимум, соответствующий m = 0.

При φ = φ₁ Δ₅ = λ, Δ₄ = 3λ/4, Δ₃ = λ/3, Δ₂ = λ/4, Δ₁ = 0, А₅ – А₃ + А₁ ≈ А₁ лучи от 4-й и 2- й щелей интерферируют с минимумом, т.к. Δ₄ - Δ₂ = λ/2. Возникает первый дополнительный максимум малой интенсивности.

При φ = φ₂ Δ₅ = 2λ, Δ₄ = 3λ/2, Δ₃ = λ, Δ₂ = λ/2, Δ₁ = 0, А₅ - А₄ + А₃ - А₂ + А₁ ≈ А₁. Возникает второй дополнительный максимум малой интенсивности.

При φ = φ₃ Δ₅ = 3λ, Δ₄ = 9λ/4, Δ₃ = 3λ/2, Δ₂ = 3λ/4, Δ₁ = 0, А₅ - А₃ + А₁ ≈ А₁ лучи от 4-й и 2- й щелей интерферируют с минимумом. Возникает третий дополнительный максимум малой интенсивности.

При φ = φ₄ Δ₅ = 4λ, Δ₄ = 3λ, Δ₃ = 2λ, Δ₂ = λ, Δ₁ = 0, А₅ - А₄ + А₃ - А₂ + А₁ ≈ А₁. Возникает главный максимум, соответствующий m = 1, главный максимум первого порядка.

Таким образом, между главными максимумами большой интенсивности возникают дополнительные максимумы малой интенсивности. Анализируя вышеперечисленные условия возникновения главных и дополнительных максимумов, можно записать общую формулу условий возникновения максимумов:

, (k = 0,1,2,3…).

Откуда можно выразить углы дифракции максимумов:

. (2)

Когда отношение 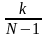принимает целое значение, мы получаем главный максимум и формула (2) принимает вид (1). Когда отношение принимает не целое значение, мы получаем дополнительный максимум. Число дополнительных максимумов равно N – 2, а число разделяющих их минимумов равно N – 1.

Дифракционные решетки содержат большое число щелей. Поэтому число дополнительных максимумов между главными максимумами велико, а интенсивность их мала. Поэтому они образуют неразличимый сплошной фон, на котором ясно видны только главные максимумы.

На интенсивность главных максимумов влияет распределение интенсивности вследствие дифракции на каждой щели, которое имеет свои максимумы и минимумы. Результирующее распределение интенсивности для N = 5 представлено на рисунке 3. Пунктирная кривая дает интенсивность от одной щели, умноженную на N². Сплошная кривая соответствует главным максимумам, а также добавочным максимумам и минимумам.

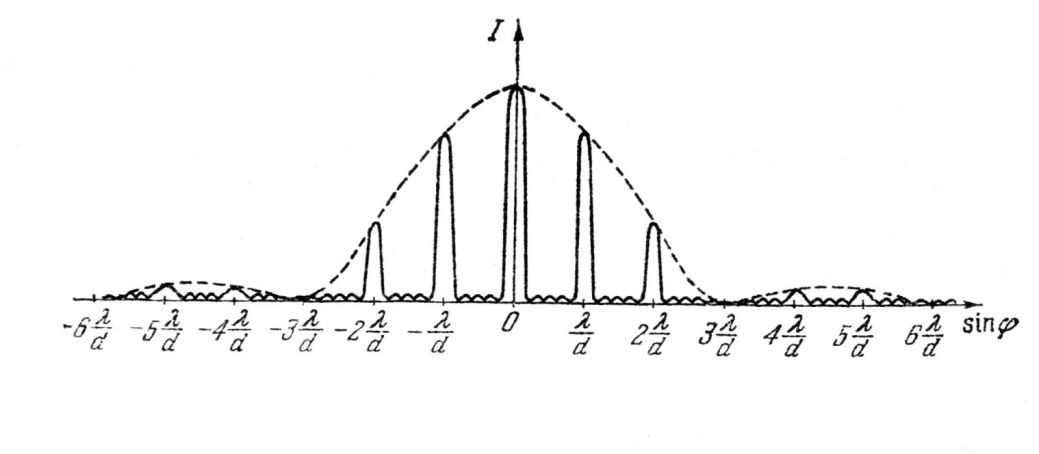
Рис. 3. Распределение интенсивности света от пяти щелей

Если источник излучает немонохроматический свет, то решетка разлагает его в спектр. При ₀ = 0 возникает максимум нулевого порядка, совпадающий для всех длин волн. По обе стороны от него возникнут спектры-максимумы порядков ±k. В спектре каждого порядка максимумы для более коротких волн расположатся ближе к нулевому максимуму. Максимумы для более длинных волн – дальше от него. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разложатся в спектр, фиолетовый конец которого обращен к центру дифракционной картины, красный – наружу. Заметим, что в то время как стеклянная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, напротив, сильнее отклоняет красные лучи.

Способность дифракционной решетки разлагать свет в спектр позволяет использовать ее для исследования спектрального состава света, т.е. дифракционная решетка используется в качестве основного элемента в дифракционных спектрометрах.

На рисунке 4 изображены схематически спектры разных порядков, даваемые решеткой при пропускании через нее белого света. В центре лежит узкий максимум нулевого порядка, у него окрашены только края. По обе стороны от центрального максимума расположены два спектра 1-го порядка, затем – два спектра 2-го порядка и т. д.

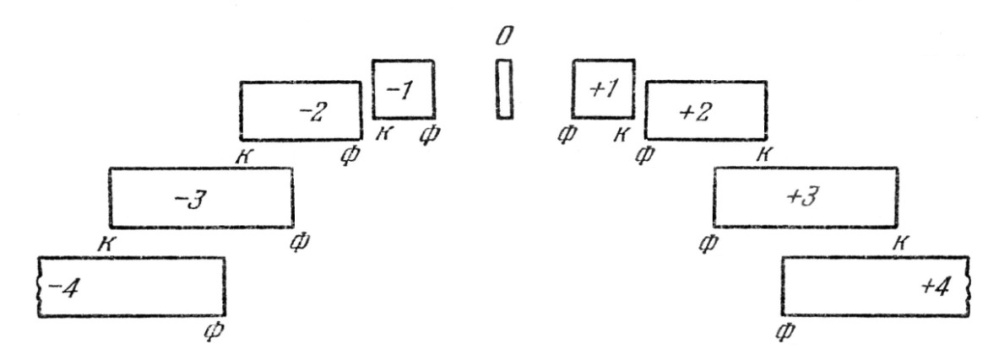
Рис. 4. Разложение белого света дифракционной решеткой на спектры до 4-го порядка

Для дифракционных решеток с большими значениями N спектры, начиная со 2-го порядка, перекрываются, спектральные линии спектра одного порядка накладываются на спектр предыдущего порядка. Идентификация линий спектра становится затруднительной, поэтому в дифракционных спектрометрах, как правило, используется спектр 1-го порядка.

Основными характеристиками дифракционной решетки являются угловая дисперсия и разрешающая способность.

Угловая дисперсия выражается в виде:

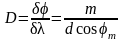, (3)

где δφ – угловое расстояние между двумя спектральными линиями, отличающимися по длинам волн на δλ, m – порядок спектра, _m – соответствующий угол дифракции.

Формула (3) может быть получена дифференцированием выражения (1).

Таким образом, угловая дисперсия характеризует протяженность спектра или способность решетки пространственно разделять световые пучки различных длин волн.

Разрешающая способность R вычисляется по формуле:

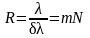, (4)

где δλ – наименьшая разница в длинах волн двух наиболее близких разрешаемых спектральных линий (λ и λ + δλ), m – порядок спектра, N – число действующих штрихов решетки.

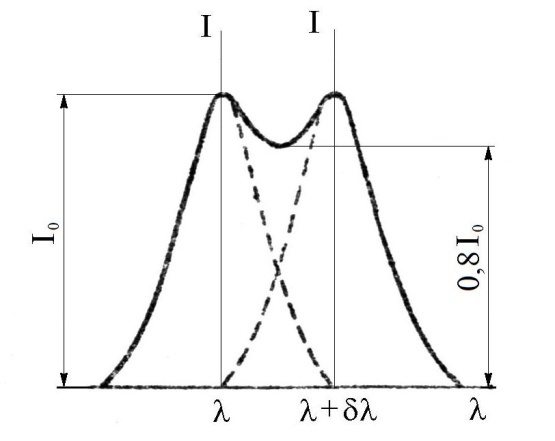
Рис. 5. Две близкие спектральные линии в положении разрешения

Разрешающая способность, определяемая соотношением (4), соответствует критерию Рэлея, согласно которому две близкие спектральные линии считаются еще разрешенными (раздельно определяемыми), если максимум (середина) одной из них совпадает с минимумом (краем) соседней. На рисунке 5 показаны графически две близкие спектральные линии в положении разрешения. Более близкие линии по критерию Рэлея считаются неразрешенными.