3.1. Виды стандартных входных сигналов (возмущений) и реакция элементов

1. Ступенчатый сигнал (рис. 3.1).

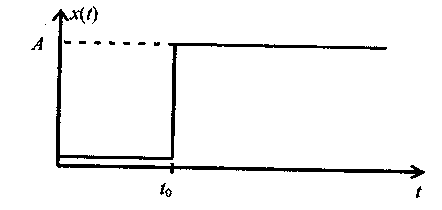
Рис. 3.1. Ступенчатый сигнал:

А - величина сигнала;

to - момент появления сигнала

Эту функцию обозначают:

x(t)=Al(t) (3.2)

где 1(t) - единичная ступенчатая функция.

Ступенчатым сигналом можно считать подачу напряжения на ка­кой-либо элемент, например, промежуточное реле, электродвигатель и т.д.

2. Импульсный сигнал (рис. 3.2).

. (3.3)

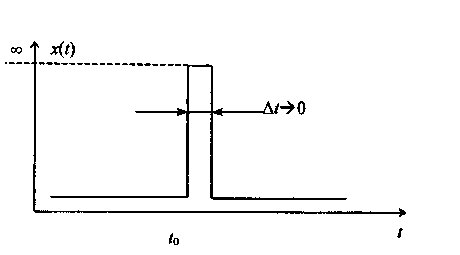
Рис. 3.2. Импульсный сигнал:

- амплитуда сигнала; - продолжительность

сигнала; А - площадь импульса

Производную от единичной ступенчатой функции

(3.4)

называют единичной импульсной или Дельта-функцией. Такой вид сигнала встречается довольно часто, например, электрический импульс продолжительностью 1тС для обычных систем регулирования напря­жения можно считать 8(t) -функцией, а для электронных - единичной ступенчатой функцией.

3. Гармонический сигнал (рис. 3.3).

На основе формулы Эйлера

(3.5)

При гармонический сигнал можно записать в комплексной форме

. (3.6)

В вещественной форме гармонический сигнал имеет более простую форму записи:

, (3.7)

где x - амплитуда входного сигнала; - круговая частота

колебаний; - начальная фаза функции x(t) .

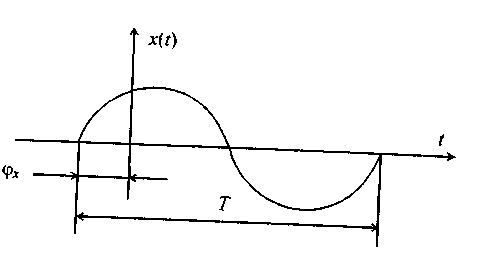
Рис. 3.3. Гармонический сигнал

В частном случае, когда , гармонический сигнал записывается

. (3.8)

Гармоническое возмущение используется в частотных методах ис­следования элементов и их систем. При разных частотах элементы по-разному реагируют на одно и то же гармоническое возмущение. Проанализировав реакцию элемента на сигналы различной частоты, можно построить частотную характеристику элемента.

Конкретный вид возмущения вызывает ту или иную реакцию эле­мента. Реакцию элемента на единичный ступенчатый сигнал называют переходной функцией h(t). Реакция элемента на 8(t) называется им­пульсной переходной или весовой функцией .

Переходную и импульсную переходную функции называют вре­менными функциями элемента.

Реакция элемента на гармоническое возмущение выражается час­тотными функциями. Если на вход линейного элемента подать гармо­нический сигнал, то по истечении некоторого времени на выходе появятся тоже гармонические колебания с той же частотой, но с дру­гими амплитудой и начальной фазой (рис. 3.4).

Рис. 3.4. Реакция элемента на гармоническое возмущение

При разных коэффициент преобразования будет различным .

Различной будет и разность фаз

(3.9)

Связь между параметрами возмущения и реакции при различных частотах описываются амплитудно-фазовой частотной характеристи­кой АФЧХ (комплексный коэффициент преобразования :

Эту функцию можно записать, используя формулу Эйлера:

(3.11)

где А) и В - вещественная и мнимая частотные функции:

Следовательно, реакция элемента

АФЧХ, или комплексный коэффициент преобразования элемента, изображается на комплексной плоскости в виде годографа (рис. 3.5).

Рис. 3.5. Комплексный коэффициент преобразования

Конец вектора описывает на комплексной плоскости кривую (годограф), которая является АФЧХ. Вектор, проведенный из начала координат в любую точку годографа, укажет амплитуду и начальную фазу, соответствующие данной частоте . С увеличением частоты сказываются инерционные свойства элемента, и выходной сигнал уменьшается. Максимальный выходной сигнал имеет место при = 0. что соответствует обычной линейной статической характеристике управления. АФЧХ объединяет два вида характеристик: амплитудно-частотную и фазочастотную.

Реакция элемента на сигнал произвольной формы оценивается с помощью принципа суперпозиции. Для этого произвольный сигнал представляется разложением в ряд Фурье.

Каждая из гармоник рассматривается отдельно, а выходной сигнал определяется как сумма воздействия каждой из них. Любую из харак­теристик динамического режима можно определить по дифференци­альному уравнению элемента. Если дифференциальное уравнение не известно, то эти характеристики можно определить экспериментально. При анализе элементов или их систем, если известны их дифферен­циальные уравнения, динамические свойства могут быть оценены с помощью передаточных функций. Передаточная функция пред­ставляет собой отношение операторного изображения выходного сиг­нала к операторному изображению входного сигнала при нулевых на­чальных условиях, когда в момент приложения возмущения (t = 0) элемент находился в состоянии покоя. При этом

(3.15)

где k=0,1,2,…,n - порядок дифференциального уравнения.

Для элемента, описанного уравнением (3.1), передаточная функция примет вид

(3.16)

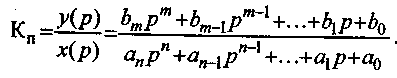
Эта функция представляет собой коэффициент преобразования элемента, выраженный в операторной форме. Зная передаточную функцию , можно определить все динамические характеристики элемента.

1. Переходная функция h(t).

Преобразование Лапласа единичной ступенчатой функции дает

(3.17)

Изображениение переходной функции имеет вид

(3.18)

Получение оригинала

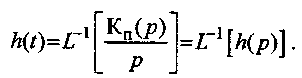(3.19)

Для стандартных функций изображения оригиналы находятся по специальным таблицам.

2. Импульсная переходная функция (t).

Преобразование Лапласа для единичной ступенчатой функции

(3.20)

поэтому изображение импульсной переходной функции

(3.21)

Таким образом, изображением импульсной переходной функции является передаточная функция элемента. Оригинал находят обратным преобразованием Лапласа.

(3.22)

3. Амплитудно-фазовая частотная характеристика (АФЧХ). Комплексный коэффициент преобразования находят простой заме­ной оператора Лапласа (р) на частоту (t).

(3.23)

Реакцию элемента на гармоническое возмущение можно опреде­лить с помощью обратного преобразования:

(3.24)