2.3.2. Параметры элементов с релейной характеристикой управления

1. Параметр срабатывания элемента ( ).

Это есть величина входного сигнала, при достижении которой про­исходит резкое изменение выходного сигнала от до (рис. 2.22). Параметром может быть напряжение, ток, сопротивление и т.д.

Рис. 2.22. Релейная характеристика управления:

, - начальное и конечное значения выходного сигнала;

, - минимальное и максимальное возможные

зна­чения выходного сигнала; и - параметры

отпускания и срабатывания; и -

максимальное и минимальное допустимые

значения входного сигнала

2. Параметр ( ).

Это есть величина входного сигнала, при достижении которой про­исходит резкое изменение выходной величины от до (рис. 2.22).

3. Коэффициент возврата элемента (Кв).

, (2.16)

определяет ширину зоны (петли) неоднозначности релейной харак­теристики.

4. Коэффициент запаса срабатывания (Кз).

. (2.17)

5. Кратность релейной характеристики (Кк).

. (2.18)

6. Коэффициент управления ( ).

. (2.19)

Этот коэффициент характеризует управляемость элемента.

На величины и оказывают существенное влияние возму-щающие воздействия , т.е.:

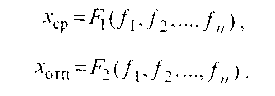(2.20)

Аналогично непрерывной характеристике управления для этих па­раметров можно записать (рис. 2.23):

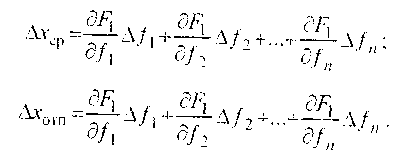(2.22)

Рис. 2.23. Влияние возмущающих воздействий на параметры

релейной характеристики

Значения Кз и с учетом возмущающих воздействий будут равны:

(2.23)

3. Динамические свойства элементов

Статические характеристики управления позволяют оценить свой­ства элемента в установившихся режимах работы. Некоторые элемен­ты автоматики могут работать не в установившихся, а в переходных режимах. При этом на вход элемента поступают непрерывно изме­няющиеся сигналы. В таких условиях элемент не успевает достичь ус­тановившегося режима, соответствующего его статической характери­стике - это и есть его динамический режим работы.

Оценка состояния элемента в динамическом режиме можнo произ­вести только с помощью дифференциальных уравнений. В тех случаях, когда это возможно. Рекомендуется заменять нелинейное дифферерциальное уравнение линейным (линеаризация элемента).

В общем случае, зависимость выходного сигнала y(t) от входного х(t) для линейных и линеаризованных элементов можно записать в операторной форме;

(3.1)

где у(р) и х(р) - операторные изображения входного x(t) и выход­ного у(t) сигналов; n, т - целые по.ложительные числа; р – оператор Лапласа; - постоянные коэффициенты, опре­деляемые свойствами и параметрами элемента.

При известном законе изменения x(t) решением уравнения (3.1) будет изменение выходного сигнала у(t). В реальных устройствах автоматики x(t) и у(t) могyт быть случайными функциями времени,

которые описываются с помощью теории случайных функций. Вход­ные сигналы могут иметь произвольный и сложный вид, что сущест­венно затрудняет анализ и синтез устройств автоматики и их элемен­тов. Для того чтобы упростить решение этих задач, в инженерной практике используют стандартные (типовые) входные сигналы.

При рассмотрении динамического режима входной сигнал называ­ют возмущением, а выходной - реакцией элемента.