5.4. Разложение случайных функций в ряд Карунена-Лоэва

Рассмотрим теперь вопрос о сходимости ряда:

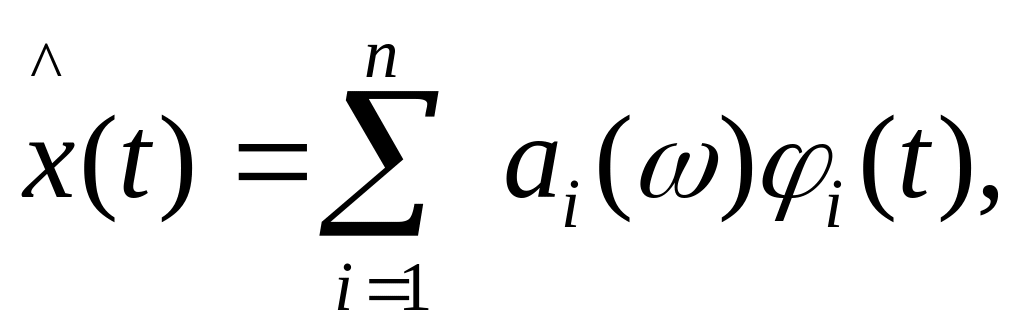(5.21)

где { }- собственные функции интегрального уравнения (5.16):

= (5.22)

где - случайный процесс с корреляционной функцией .

Пусть в разложении (5.21) -конечно, тогда равенство (5.21) является приближенными почти для любой выборочной функции

(5.23)

где - случайный процесс.

Вычисляя

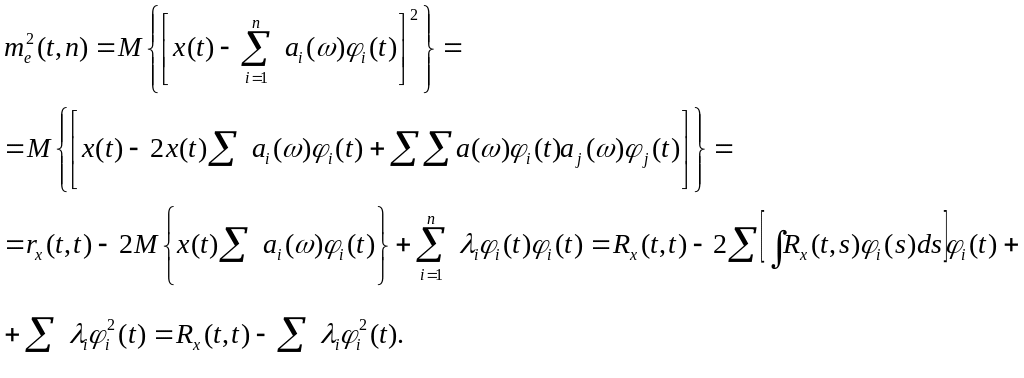
И так как (свойство 7)

то (5.25)

или

(5.26)

но и ограничена, а Отсюда следует, что

Определение 5.1.

Разложение случайного процесса в ряд (5.21) по собственным функциям интегрального уравнения (5.16) называют разложением Карунена-Лоэва. Оно обеспечивает представление случайного процесса посредством некоррелированных случайных величин Полезность разложения Карунена-Лоэва объясняется следующими двумя обстоятельствами:

1. во многих задачах теоретического анализа случайных функций разложение используется в качестве математического инструмента. В большинстве таких задач собственные функции и собственные значения не входят в окончательный результат, что позволяет не находить в явном виде;

2. в задачах, связанных с практическим применением, для получения удовлетворительного по точности результата достаточно знания одной или нескольких собственных функций и собственных чисел.

5.4.1. Представление винеовского процесса в виде разложения Карунена-Лоэва.

Пусть - винеровский процесс, определенный при Как отмечалось в п. п. 1.3, ему присущи следующие свойства:

Приращения случайного процесса являются независимыми, т. е. если то и статистически независимы.

Интегральное уравнение (5.16) имеет вид

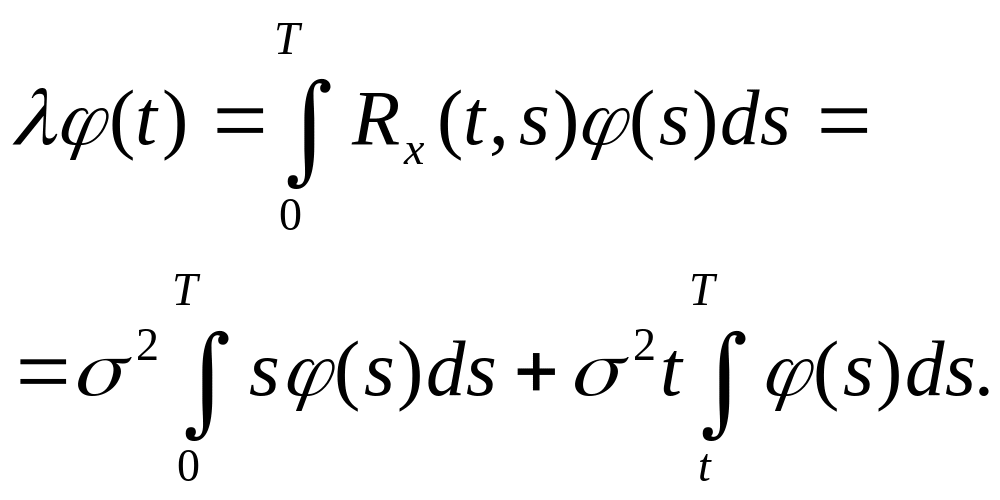(5.27)

Преобразуем интегральное уравнение в соответствующее дифференциальное. Дифференцируя обе части по , получим

так как

то

Дифференцируя повторно, получим

Или при

(5.28)

Существует три возможные области изменения : <0; =0; >0. Можно убедиться непосредственно, что области <0, =0 не дают решений, удовлетворяющих интегральному уравнению (5.27) (это же следует из свойств интегральных уравнений с невырожденным, симметричным, положительно определенным ядром [6]. Более того, в силу (5.20)).

Общее решение дифференциального уравнения (5.28) в этом случае [6]:

(5.29)

где (5.30)

Подставляя (5.29) и (5.30) в (5.28), получим, что и решениями интегрального уравнения будут собственные числа и собственные функции:

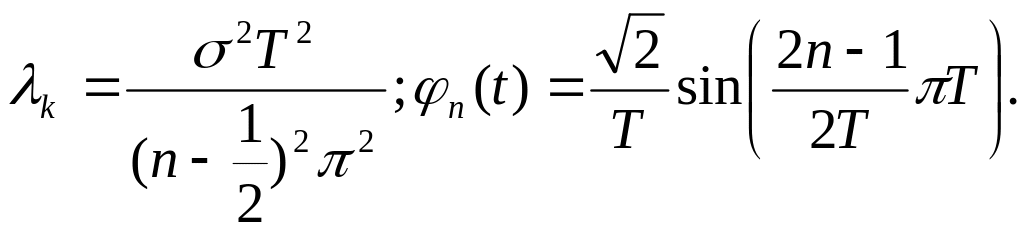(5.31)

5.4.2. Представление процесса типа белого шума

Используя полученный выше результат, представим винеровский процесс в виде ряда

(5.32)

причем (5.33)

Для фиксированного продифференцируем Получим

(5.34)

Обозначим тогда в силу ортонормированности функции

ряд(5.33) можно рассматривать как разложение выборочной функции процесса в ряд по ортогональным функциям.

Так как определено выражением (5.33), то легко видеть, что

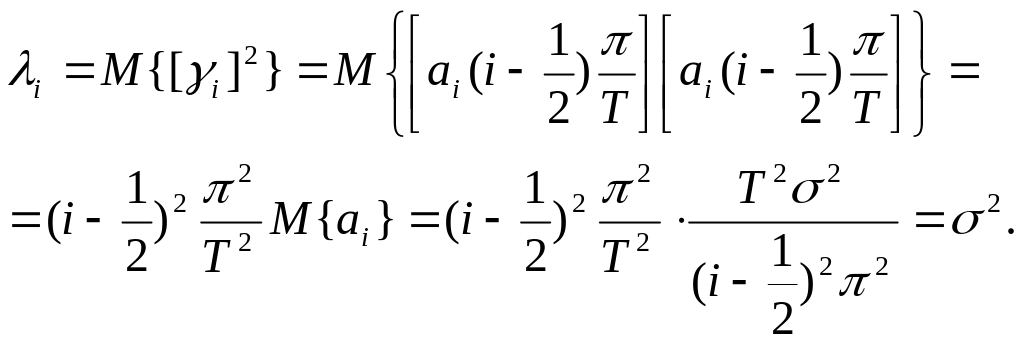(5.35)

То есть для случайного процесса , полученного дифференцированием винеровского процесса, все собственные числа интегрального уравнения равны. Очевидно, что если в (5.34) положить , то ряд не будет сходиться. Кроме того, при и, следовательно, случайный процесс (5.34) должен обладать бесконечной энергией.

Получим корреляционную функцию процесса , дифференцируя

(5.36)

Корреляционная функция случайного процесса является - функцией.

Запишем интегральное уравнение (5.16) для случайного процесса

(5.37)

это уравнение в сил свойств - функции выполняется для любых , причем Следовательно, любой ряд ортонормированных функций пригоден для разложения этого процесса.

Итак, процесс типа белого шума имеет следующие свойства:

Свойство 1. Корреляционная функция случайного процесса типа белого шума является - функцией.

Свойство 2. Случайный процесс типа белого шума можно разложить на интервале в любой полный ряд ортонормированных функций.

Свойство 3. Коэффициенты разложения белого шума в ряд по отонормированным функциям некоррелированы и имеют одинаковые дисперсии.

Свойство 4. Если коэффициенты разложения случайного процесса в ряд некоррелированы и имеют равные дисперсии, то процесс называют белым шумом.