3.3. Процесс чистого размножения

Предположим, что в процессе Пуассона вероятность одного события за время (t, t+ h) зависит от числа событий за время (0, t ). Такой процесс можно рассматривать как пуассоновский процесс с переменной интенсивностью, характеризующейся последовательностью λ_0, λ₁, λ₂, ……

Удобной формой описания процесса Пуассона является описание его в пространстве состояний.

Пусть на время (0, t ) произошло n событий. Будем говорить, что в этом случае система находиться в состоянии E _n. Если за время h произойдет очередное событие, то система перейдет в состояние E _n+1. В противном случае система останется в состоянии E _n.

Определение 3.1.

Пуассоновский процесс, для которого переход из состояния E _n возможен только в состоянии E _n+1, называется процессом чистого размножения [ 5 ].

Если в момент t система находиться в состоянии E _n (n = 0,1, 2, ….), то вероятность того, что за время (t, t+ h) осуществляется переход в E _n+1, как это следует из (3.2 ), равна λ _n h + 0 (h). Вероятность иных изменений имеет более высокий порядок малости, чем h.

Дифференциальные уравнения (3.4 ) и (3.5 ) имеют для процессов чистого размножения следующий вид:

Р' _n (t) = – λ _n Р _n (t) + λ _n-1Р_n-1(t);

Р₀ (t) = – λ ₀ Р ₀ (t) (n ≥ 1 ) (3.7 ) Начальным состоянием системы является E ₀ , причем Р ₀ (0) =1, а Р ₀ (t) = e ^{- λ} ₀^t.

Можно, однако, в начальный момент времени рассматривать систему в любом состоянии.

Обобщим рассмотренный процесс размножения. С этой целью предположим, что в системе возможны переходы из E _n но только в E _n+1, но и в состояние E _n-1 . Конечно, в этом случае состояние E _n уже нельзя трактовать как число событий, реализованных на отрезке ( 0,t ).

Процесс такого вида впервые был изучен в биологии, где с его помощью опи-сывались процессы рождения и гибели. Поэтому иногда такие процессы называют процессами " гибели и размножения" [ 5 ].

В задачах анализа и синтеза АСУ такие процессы находят достаточно широкое применение. Поэтому рассмотрим их подробнее.

3.4. Пуассоновские процессы в системах массового обслуживания

Начнем с содержательного примера, имеющего большое значение для анализа и синтеза АСУ.

Пример 5. Рассмотрим вычислительную систему коллективного пользования, функционирующую в диалоговом режиме ( рис. 5 ).

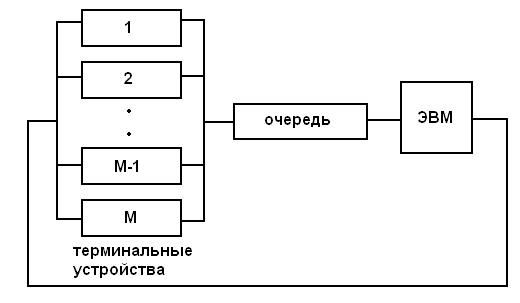
Рис.5. Вычислительная система коллективного пользования

В этой вычислительной системе каждое терминальное устройство может находиться в одном из двух режимов: " активное ожидание" и " пассивное ожидание". В режиме активного ожидания терминальное устройство ожидает разрешения на ввод очередного сообщения в ЭВМ. Если ЭВМ свободна, то она немедленно приступает этого сообщения. В противном случае сообщение помещается в очередь, где ожидает в течение некоторого времени.

Пусть любое терминальное устройство, находящееся в режиме пассивного ожидания, может быть активизировано в интервале времени (t, t+ h) с вероятностью λ h + 0 (h), причем активизация терминалов происходит независимо друг от друга. Таким образом, если терминал пассивен в момент времени t, то промежутки времени от t до его активизации имеют распределение Пуассона (3.6)

Суммарный поток событий (поток переключений ) будет являться процессом чистого размножения с интенсивностью

при 0 ≤ n ≤ М, ( 3.8)

при n > М.

Предположим теперь, что времена обработки представляют собой случайные числа, имеющие экспоненциальное распределение e ^{–μ t} .

Другими словами, вероятность того что время обслуживания очередного сообщения будет больше, чем t, есть e ^{–μ t}. Из выражения ( 3.6 ) видно, что e ^{–μ t} представляет собой распределение Пуассона при n = 0.

Предполагая, наконец, что интервалы времени обработки сообщений взаимно независимы, придем к математической модели, описывающей функционирование вычислительной системы коллективного пользования в диалоговом режиме.

Для рассмотренного примера удобно вновь ввести пространство состояний, считая, что система находится в состоянии E _{n ,}, где n – общее число обслуживае-

мых и ожидающих в очереди сообщений, n = 0, 1, 2, … , М.

Ясно, что в такой системе из состояний E _n+1 возможны переходы как в E _n+1 так и в E _n-1. В силу малости члена 0 (h ) в уравнении ( 3.2 ) переходы в системе возможны лишь в ближайшие, соседние состояния. Если в некоторый момент система находится в состоянии E _n, то вероятность того, что за время (t, t + h) осуществляется переход E _n → E _n+1, равна λ _n h + 0 (h), а вероятность перехода E _n → E _n-1 (при n ≥ 1 ) равна μ h + 0 (h ). Вероятность того, что за время (t, t + h) осуществляется более чем одно изменение, имеет порядок малости более высокий, чем h .

Для вывода дифференциальных уравнений, описывающих поведение такой системы, предположим, что в момент времени t вероятность пребывания системы в состоянии E _n равняется P _n ( t ) . Для вычисления P _n ( t + h) заметим, что система может находиться в момент времени t + h в состоянии E _n в следующих трех случаях :

1. в момент t система находится в E _n и за время h не происходит никаких изменений;

2. в момент t система находится в E _n-1 и затем переходит в E _n;

3. в момент t система находится в E _n+1, к моменту ( t + h) система переходит в состояние E _n .

По предположению, вероятность двух и более переходов за время h равняется 0 (h ). Кроме того, первые три возможности – взаимно исключающие и вероятности их можно складывать. Поэтому

P _n ( t + h) = P _n ( t )[ 1 - λ _n h - μ h ] + λ _{n –1} h P _n-1 + μ _n+1 h P _n+1 + 0 (h ).

Перенося P _n ( t ) влево и разделив на h , получим при h → 0

P¹ _n ( t ) = - (λ _n + μ _n ) P _n ( t ) + λ _{n –1} P _n-1 ( t ) + μ _n+1 P _n+1( t ). ( 3.9)

Аналогично выводятся уравнения для n = 0, и n = М:

P¹ ₀ ( t ) = - λ ₀ P ₀ ( t ) + μ ₁( t );

P¹ _M ( t ) = - μ _n P _M ( t ) + λ P _m-1( t ). (3.10) Если в момент t = 0 система находится в состоянии i, то должны выполняться начальные условия ( 0 ) = 1, = 0 при n ≠ i.

Система дифференциальных уравнений ( 3.10 ) выведена для λi, μi, произвольно зависящих от n . В большинстве случаев зависимости λ_{( n)} и μ_{( n )} имеет специальный вид. В частности для примера 5

λ_n = (μ – n)λ , μ_n = μ и дифференциальные уравнения принимают вид:

P¹ ₀ ( t ) = - мλ P ₀( t ) + μ P ₁ ( t );

P¹ _n ( t ) = -[ ( М – n )λ + μ ] P_n( t ) + … + μ P _n+1 ( t ) (3.11 )

P _M ( t ) = - μ P _M ( t ) + λP _{м -1}( t ).

Эта линейная система дифференциальных уравнений, которая может быть решена обычными методами. При t → ∞ и ограниченных λ, μ, м система ( 3.11 ) имеет единственное решение [ 5 ], причем пределы

Существуют не зависят от начальных условий.

Предельные вероятности P _n удовлетворяют системе линейных уравнений, получаемых из ( 3.11 ), если положить в них P¹ _n ( t ) = 0. Для P _n из ( 3.11 )

при P¹ _n ( t ) = 0 легко вывести рекуррентную формулу

( М – n ) λ P _n = μ P _n + 1 (3.12)

Полагая n = М – 1, М = -2, … , 1, 0 , получаем

(3.13)

Неизвестную постоянную P _M можно определить из условий, что сумма P

равна единице. Легко видно, что

(3.14)

Вероятность P ₀ может интерпретироваться для примера 5 как вероятность того, что ЭВМ не занята. Математическое ожидание числа сообщений, стоящих в очереди, равно

(3.15)

Так как P ! в сумме дают единицу, получим, используя (3.14 ), что

(3.16)

или

4. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ

С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ

4.1. Свойства корреляционных функций случайных процессов

с непрерывным временем.

В этом разделе мы подробно изучим введенную в п.п. 1.1 корреляционную функцию случайных процессов . Напомним, что корреляционная функция случайного процесса – это функция двух аргументов :

(4.1)

На практике часто используют нормированную корреляционную функцию

(4.2)

Последняя функция удобна тем, что ее значения находятся в пределах ± 1 и, следовательно, по абсолютной величине можно судить о степени связности (зависимости) двух ординат случайного процесса.

Непосредственно из определения корреляционной функции (4.1) следует, что корреляционная функция симметрична

(4.3)

Это обстоятельство позволяет ограничиться областью аргументов t≥ s или s ≥ t. Корреляционная функция случайного процесса удовлетворяет неравенству

(4.4)

Корреляционная функция обладает очень важным свойством, позволяющим существенно облегчить анализ случайных процессов, свойством положительной определенности [6 ]. Смысл этого свойства в следующем. Рассмотрим интеграл

(4.5)

где - некоторые произвольные функции.

Подставив в (4.5) выражение корреляционной функции (4.1), меняя местами операции интегрирования и математического ожидания, получим

где

Последнее выражение можно записать теперь в виде:

Но математическое ожидание неотрицательной величины не может быть отрицательным и, следовательно, при любой области интегрирования Т и при любой функции интеграл (4.5) не меньше нуля. Функция , обладающие таким свойством, называются положительно определенными функциями.