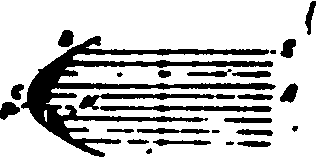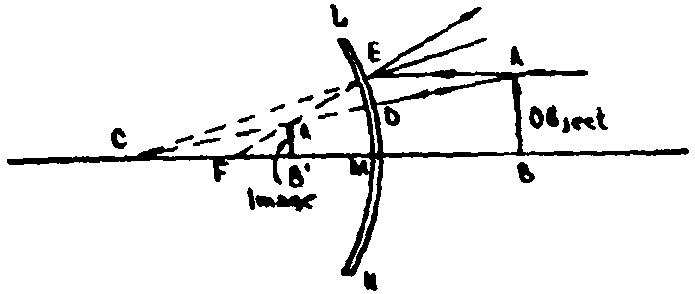
Construction of images in a convex mirror

In case of a convex mirror (Fig. 9) both the center of curvature and the principal focus arc behind the mirror. Let AD be the object as in the preceding case, and draw from A the ray AE parallel to the principal axis ВС After being reflected at E this ray leaves the mirror as if it came from F, the principal focus behind the mirror. Now draw AD perpendicular to the surface of the mirror, which will be reflected from the latter at D and will appear to have come from C, the center of curvature behind the mirror. At A', where the backward extensions of the two rays intersect, there is formed a virtual image of the point A. On locating the images of the other points in AB in the same way it will be found that the object AB forms the image A'B', the latter lying behind the mirror LN and being virtual, erect and diminished in size.

Fig. 9 Image in a convex mirror. The image is virtual, diminished and upright

Fig. 10 Derivation of mirror formula.

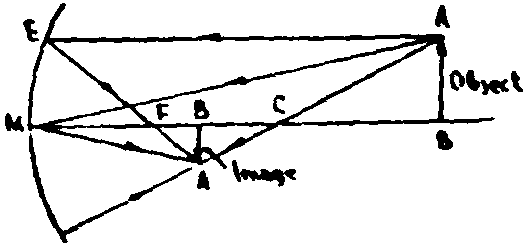
Size of Object and Image

With both the convex or the concave mirror there is a definite relation between the size of the image and that of the object, which relation is quite simple in either case. In Fig 10, the triangles given (ABM and A'B'M') are equiangular and, consequently, similar, the acute angles being the angles of incidence and the angles of reflection, respectively. It follows that the corresponding sides of the triangles are necessarily proportional. Hence, the resulting formula is simple:

size of image	=	distance of image from the mirror	=	v
size of object		distance of object from mirror		u

Parabolic mirrors

If the width of a mirror (Fig. 11) is comparable to its radius of curvature, parallel rays which have been reflected do not meet at the single point F, that is, the principal focus. Rays reflected from a limited region of the mirror in the neighborhood of its vertex M are brought to a focus at F whereas those which strike the mirror at points distant from the vertex of the mirror cross the axis at points other than F and nearer to the mirror, and are not brought to a focus. This has the effect of destroying the definition sharpness of the image which would otherwise be formed by the mirror.

If the section of the mirror is a parabola instead of a circle, parallel rays are

Fig. 11 Spherical aberration on a spherical mirror.

Fig. 12 Parabolic mirror corrects for spherical aberration.

bound to be all focused at a single point after reflection (Fig. 12). On the other hand, a point source of light at the focus will send out parallel rays after reflection from the. surface of the mirror. The chief advantage of a parabola lies in the fact that a line FB (Fig. 13) through the focus as well as a line BS parallel to the axis make equal angles with the normal. This results in all rays parallel to the axis CA passing through the point F after reflection so that the whole beam, however large, will be brought to a common focus. The distortion found in the spherical mirror is thus avoided. Since mirrors to be used for searchlights must be of large apertures, parabolic mirrors are very useful and widely used for such purposes.

Whenever the source of light is placed inside the focus of a parabolic mirror (Fig. 14), the rays of light diverge after reflection; whenever it is outside the focus, the rays converge after reflection. This fact is sometimes of importance, e.g. in the adjustment of some kinds of lights, such as the headlights of a motor car.

Fig. 13 Parabolic mirror. Source of light at the principal focus.

Fig. 14 Parabolic mirror. Light not at the principal focus.