1.6 Критерии, используемые при оценке точности измерений.

При выборе критерия для оценки наблюдений необходимо пояснить, что на практике результат считается одинаково ошибочным, будет ли он больше истинного значения или меньше. Поэтому стараются установить такой критерий оценки точности наблюдений, который не зависел бы от знаков отдельных погрешностей и заметно отображал наибольшие из них.

Таким требованиям удовлетворяет средняя квадратическая погрешность так как

1) на величину средней квадратиче­ской ошибки сравнительно сильно влияют большие по абсолютной ве­личине случайные ошибки, т. е. как раз те, которые и определяют собой степень надежности полученных результатов измерений;

2) средняя квадратическая ошибка устойчива, так что практически достаточно срав­нительно небольшого числа измерений, чтобы определить значение этой ошибки с удовлетворительной степенью точности*;

3) по средней квадратической ошибке можно судить о «Предельной ошибке», возможной при данных условиях измерений.

Когда известно истинное значение X измеряемой величины, среднюю квадратическую погрешность отдельного результата измерений находят по формуле Гаусса :

,

где ∆_i= l_i – Х;

l_i – результат i измерения величины истинное значение которой равно Х;

i = 1,2,3,…..n.

Когда истинное значение искомой величины неизвестно среднюю квадратическую погрешность отдельного результата измерений определяют через отклонения от арифметической средины δ по формуле Бессели:

, (2)

где δ_i = l_i - l_ср ; l_ср = ∑ l_i /n

Так как величина погрешности i- го измерения характеризуется средней квадратической погрешностью m_i то квадрат средней квадратической погрешности арифметической средины

Принимая во внимание, что наблюдения равноточны, можно положить, что

m₁ = m₂ = ... = m_n = m.

Тогда М ² = m ²/ п,

откуда

Следовательно, средняя квадратическая погрешность арифметической средины в раз меньше средней квадратической погрешности отдельного измерения.

Применительно к конкретным условиям измерений указывают критерий отбраковки результатов наблюдений. В качестве такого критерия принимают предельную погрешность ∆ _пр. При более ответственных измерениях

∆ _пр = ±2m .

Для менее ответственных измерений такая погрешность будет составлять

∆ _пр = ±3m.

Погрешность, определяемая по данным формулам , является абсолютной.

В практике геодезических измерений точность наблюдений принято характеризовать не только абсолютным значением погрешности (истинной, средней квадратической), но и ее относительной величиной. В качестве относительной погрешности принимают отношение ср. кв. погрешности к значению измеряемой величины:

∆ _отн = m / l = 1 / ( l /m) .

где l — значение измеряемой величины.

1.7 Основные «единичные» построения в геодезии или способы съемки ситуации местности

Одной из главных задач геодезии является определение координат точек на земной поверхности в соответствующих системах координат.

При геодезических измерениях всегда положение одной точки определяется по отношению к другим точкам местности.

Обозначенные на местности точки, от которых выполняют геодезические измерения, называются исходными или опорными. Точки, положение которых на местности необходимо определить, называют определяемыми.

Исходные и определяемые точки могут располагаться в горизонтальной плоскости в плане (плановые точки) и вертикальной — по высоте (высотные точки).

Рассмотрим семь основных геодезических способов построения, применяемых для определения положения точки в плане и по высоте.

Требуется определить положение точки С относительно обозначенных на местности исходных точек А и В.

1. Положение точки С (рис. 1.7.1 а ) можно определить, если опустить из этой точки перпендикуляр на прямую АВ, а затем измерить расстояние l от точки А до основания перпендикуляра и длину перпендикуляра d. Отрезки l и d будут координатами точки С. Такое построение называют способом перпендикуляров.

Если прямую АВ принять за ось абсцисс прямоугольной системы координат, то перпендикуляр d будет ординатой определяемой точки, а расстояние l — ее абсциссой. Поэтому способ называют также способом ординат.

Рис. 1.7.1

b

В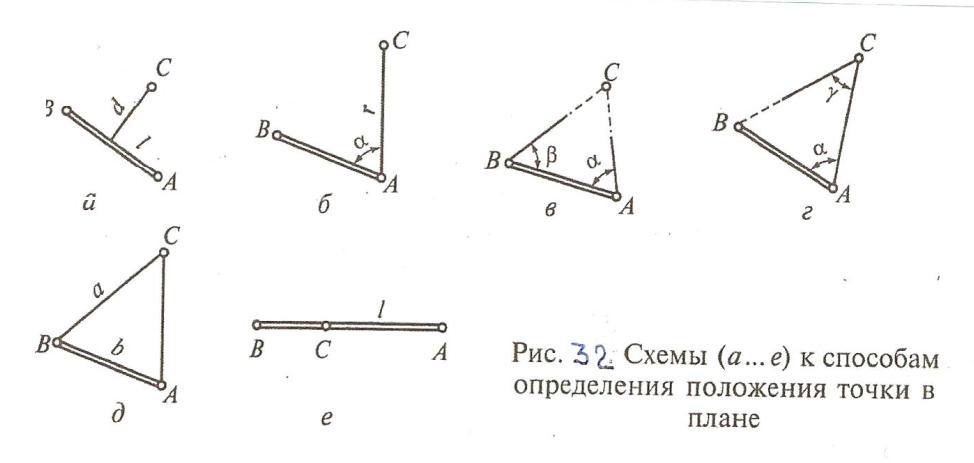

2. Положение точки С (рис. 1.7.1 б) определяется, если измерить на точке А угол α и длину АС — r. Такой способ называют способом полярных координат: полярные координаты точки С — α и r, угол α — полярный, точка А — полюс, прямая АВ — полярная ось, отрезок r — радиус-вектор.

3. Для определения положения точки С (рис. 1.7.1, в) относительно прямой АВ достаточно измерить углы α и β на точках А и В.Этот способ называют прямой угловой засечкой (прямая АВ — базис засечки).

4. Положение точки С (рис. 1.7.1 г) определяется, если измерить угол α из точки А и угол γ на определяемой точке С (способ боковой засечки).

5. Для определения положения точки С (рис. 1.7.1 д) можно измерить длину линий АC- b и ВС = а (способ линейной засечки).

6. Точка С (рис. 1.7.1 е) находится на линии АВ (в створе АВ) и на расстоянии l от точки А (способ створно-линейной засечки).

7. Положение определяемой точки С по высоте (рис. 1.7.2.) находят, измерив ее превышение h над исходной точкой А (геометрическое нивелирование) или угол наклона v линии АС к горизонту и горизонтальное проложение d (проекцию линии АС на горизонтальную плоскость), или расстояние АС (тригонометрическое нивелирование).

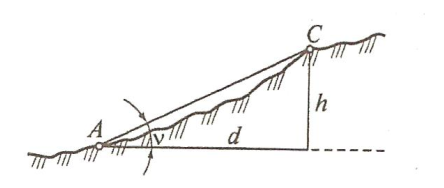
Рис. 1.7.2 Схема к способу определения положения точки по высоте

«Одиночные» построения выполняют, если расстояния между точками сравнительно невелики и есть непосредственная видимость между исходными и определяемыми точками. Когда расстояния между исходными точками значительны или требуется найти положение нескольких точек, пользуются более сложными построениями называемые в геодезии ходами или сетями.