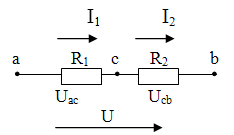
Свойства последовательного соединения элементов.

а) Последовательное соединение резисторов

1. Эквивалентное (общее) сопротивление цепи равно

сумме сопротивлений элементов (резисторов)

R_Э= R₁+ R₂.

2. Через все элементы цепи протекает одинаковый ток

I = I₁ = I₂.

3. Напряжение, приложенное к цепи, равно сумме нап-

ряжений на отдельных участках

U_ab = U_ac + U_cb.

б) Последовательное соединение конденсаторов

Общая емкость C_общ батареи конденсаторов при последовательном соединении конденсаторов определяется по формуле

в) Последовательное соединение источников ЭДС

При последовательном соединении гальванических элементов электродвижущая сила (ЭДС) батареи равна сумме ЭДС отдельных элементов.

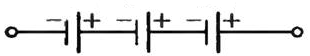
Такое соединение допускается для элементов, имеющих одинаковые ЭДС и внутренние сопротивления R_вт. Последовательное соединение применяется в случае, когда напряжение потребителя больше ЭДС одного элемента батареи, а ток потребителя не превышает номинального тока элемента.

Свойства параллельного соединения элементов

а) Параллельное соединение резисторов

1. Напряжения, приложенные к каждому из параллельно соединенных элементов, равны между собой

U = U_R1 = U_R2.

2. Cуммарный ток цепи равен сумме токов отдельных ветвей:

I = I₁ + I₂.

3. Эквивалентное сопротивление цепи R_Э определяется по формулам

,

где G₁ и G₂ – электрические проводимости ветвей.

4. Эквивалентная проводимость цепи равна сумме проводимостей ветвей

G_Э = G₁ + G₂.

б) Параллельное соединение конденсаторов

Общая емкость C_общ батареи конденсаторов при параллельном соединении равна сумме емкостей отдельных конденсаторов:

С_общ = С₁ + С₂ + С₃.

Смешанное соединение резисторов

Смешанное соединение резисторов представляет собой комбинацию последовательного и параллельного соединений.

Преобразование (свертывание) цепи начинаем с параллельно соединенных резисторов R₂ и R₃

а )

Эквивалентное сопротивление : .

Далее последовательно соединенные резисторы R₁ и R₂₃ заменяются эквивалентным сопротивлением R_э (рисунок б).

б )

Эквивалентное сопротивление Rэ: .

Правила замены различных схем соединения эквивалентными схемами приведены в табл. 1. После каждого этапа преобразования рекомендуется заново начертить цепь с учетом выполненных преобразований (табл. 2).

Таблица 1

Эквивалентные преобразования простейших электрических цепей

Таблица 2

Пример расчета электрической цепи методом эквивалентных преобразований

Эквивалентные преобразования треугольника в звезду

В сложных цепях преобразование треугольника в эквивалентную звезду упрощает расчетную схему и позволяет свести ее к схеме смешанного соединения сопротивлений. По условию эквивалентности преобразований токи и напряжения непреобразованной части цепи не должны измениться.

Пример. Рассчитать токи в ветвях цепи методом эквивалентных преобразований.

Рис. 3.2. Исходная электрическая цепь

В рассматриваемой цепи есть участки, где соединения сопротивлений нельзя отнести ни к последовательным, ни к параллельным соединениям (треугольники АВД и АВК).

Для упрощения схемы заменим треугольник АВД эквивалентной звездой А'В'Д'.

Последовательность расчета

1. Произвольно задаем направление токов в ветвях и определяем узлы и контуры электрической цепи.

2. Заменяем треугольник АВД на эквивалентную звезду А'В'Д'.

Рис. 3.3. Преобразованная расчетная цепь

В результате получаем три параллельных ветви между узлами K и N

R₁, R₄₆ (1-я ветвь)

R₄₅, R₂, R₇ (2-я ветвь)

R₃, R₅₆ (3-я ветвь).

3. Рассчитываем сопротивления лучей эквивалентной звезды по формулам из табл.1

R₄₆ = ; R₅₆ = ; R₄₅ = .

4. Далее производим эквивалентные преобразования (свертывание) цепи.

Ветви содержат по 2-3 последовательно соединенных элемента.

Эквивалентное сопротивление первой ветви: R_э1= R₁ + R₄₆ ( ток I₁).

Эквивалентное сопротивление второй ветви: R_э2= R₂ + R₇ + R₄₅ ( ток I₂).

Эквивалентное сопротивление третьей ветви: R_э3= R₃ + R₅₆ ( ток I₃).

5. После эквивалентных преобразований представляем расчетную цепь в виде:

б)

Сопротивления R_Э2 и R_Э3 соединены параллельно, и эквивалентное сопротивление R_Э4 определяем по формуле

.

в )

Сопротивления R_Э1 и R_Э4 соединены последовательно, и эквивалентное сопротивление всей цепи будет

г)

Ток определяем по формуле

6.Далее определяем падение напряжения на участке KN: U_KN= I₁ R_Э4.

Токи I₂ и I₃ находим по закону Ома для участка цепи:

.

7. Далее возвращаемся к исходной электрической цепи для расчета токов I₄, I₅, I₆.

Выполняем расчет оставшихся токов с использованием законов Кирхгофа.

Составляем уравнение по второму закону Кирхгофа для контура АКВ:

E₁= R₁I₁+ R₆I₆-R₃I_3.

Составляем уравнения по первому закону Кирхгофа для узлов А и В:

узел А: I₁ – I₆ – I₄=0

узел В: I₃+I₅+I₆=0.

Решив систему уравнений, находим токи I₄, I₅ и I₆.

Для проверки правильности расчета составляем баланс мощностей

E₁I₁=I₁²R₁ + I₂² (R₇+R₂) + I₃²R₃+I₆²R₆+I₄²R₄+I₅²R₅ (см. стр. 29).

Метод эквивалентного генератора (активного двухполюсника)

Метод эквивалентного генератора рационально применять, если необходимо найти ток в одной ветви сложной электрической цепи, не рассчитывая токи в других ветвях. Он дает возможность часть сложной электрической цепи с источниками энергии и двумя выделенными выводами ab, то есть активный двухполюсник А заменить эквивалентным генератором. ЭДС эквивалентного генератора равна напряжению холостого хода на выводах двухполюсника, а внутреннее сопротивление – входному сопротивлению двухполюсника. Если в активный двухполюсник входят все элементы схемы, кроме одного выделенного сопротивления R, то можно найти ток I в этом сопротивлении.

Для расчета тока в сопротивлении R следует сначала отключить это сопротивление и определить напряжение U на выводах по методу двух узлов. Далее нужно исключить все ЭДС в оставшейся части схемы и найти ее сопротивление относительно выводов отключенного сопротивления и выполнить расчет искомого тока.

Пример: Для схемы по рисунку а) заданы ЭДС и сопротивления: E₁=100В, E₂=24В, R₁=5 Ом, R₂=2 Ом, R₃=10 Ом.

Найти ток в ветви с сопротивлением .

a)

Решение: Отключаем

сопротивление и находим напряжение холостого хода на выводах a b двухполюсника по методу двух узлов (рис. б).

б )

В;

; - активные проводимости ветвей двухполюсника.

Входное сопротивление между выводами a b при исключенных

ЭДС и

Ом

(сопротивления и включены параллельно, рис. в).

в )

Ток А.

Расчет электрической цепи методом непосредственного

применения законов Кирхгофа

Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:

Согласно второму закону Кирхгофа алгебраическая сумма падений напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС,входящих в этот контур:

Расчет многоконтурной линейной электрической цепи, имеющей "b" вет-

вей с активными и пассивными элементами и "у" узлов, сводится к определе- нию токов отдельных ветвей и напряжений на зажимах элементов, входящих в данную цепь.

Пассивной называется ветвь, не содержащая источник ЭДС. Ветвь, со- держащая источник ЭДС, называется активной.

1-й закон Кирхгофа применяют к независимым узлам, т.е. таким, которые отличаются друг от друга хотя бы одной новой ветвью, что позволяет получить (y - I) уравнений.

Недостающие уравнения в количестве b - (у - I) составляют, исходя из второго закона Кирхгофа. Уравнение записывают для независимых контуров, которые отличаются один от другого, по крайней мере, одной ветвью.

Порядок выполнения расчета:

- выделяют в электрической цепи ветви независимые узлы и контуры;

- с помощью стрелок указывают произвольно выбранные положительные направления токов в отдельных ветвях, а также указывают произвольно вы- бранное направление обхода контура;

- составляют уравнения по законам Кирхгофа, применяя следующее пра- вило знаков:

а) токи, направленные к узлу цепи, записывают со знаком "плюс", а токи, направленные от узла,- со знаком "минус" (для первого закона Кирхгофа);

б) ЭДС и напряжение на резистивном элементе (RI) берутся со знаком "плюс", если направления ЭДС и тока в ветви совпадают с направлением обхода контура, а при встречном направлении - со знаком "минус";

- решая систему уравнений, находят токи в ветвях. При решении могут быть использованы ЭВМ, методы подстановки или определителей.

Отрицательные значения тока какой-либо ветви указывают на то, что выбранные ранее произвольные направления тока оказались ошибочными. Это следует учитывать, например, при построении потенциальной диаграммы, где следует знать истинное направление тока.

На рис. 3.4, а изображена исходная электрическая схема, для которой сле- дует рассчитать токи в ветвях. Направления токов и обхода контуров приведены на рис. 3.4, б.

а) б) Рис. 3.4

Система уравнений, составленных по первому и второму законам Кирхгофа, имеет вид

Расчет электрической цепи методом контурных токов

При расчете цепи методом контурных токов выдвигаются два предполо- жения:

- в каждом контуре протекают независимые друг от друга расчетные (контурные) токи;

- ток каждой ветви равен алгебраической сумме контурных токов, протекающих через эту ветвь.

Рассмотрим схему, представленную на рис. 3.5.

Рис. 3.5

При расчете рекомендуется следующая последовательность действий:

- находят в цепи ветви, узлы и контуры;

- указывают произвольные направления токов в ветвях и направления обхода контуров;

- произвольно выбирают направления контурных токов, обычно совпадающие с направлениями обхода контура;

- для независимых контуров составляют уравнения по второму закону Кирхгофа относительно неизвестных контурных токов I₁, I₁₁, I₁₁₁.

Для рассчитываемой электрической цепи система уравнений будет иметь вид

для контура acef: (R₁ + R_вт1 + R₃) I_I – R₃ I_II =E₁

для контура abc: -R₃ I_I + (R₂ + R₃ +R₄) I_II - R₂ I_III = -E₂

для контура bdc: -R₂ I_II + (R₂ + R₅ +R₆) I_III = E₂.

В рассматриваемом примере при составлении уравнений принято во вни- мание то, что вторая (R₂, E₂) и третья (Rз) ветви электрической цепи являются смежными и по ним протекают два контурных тока, каждый из которых обусловливает на резисторе смежной ветви падение напряжения, например, R₂I_II и R₂I_III (для токов второй ветви).

R_вт1 – внутреннее сопротивление источника ЭДС Е₁.

Токи в ветвях определяют алгебраическим суммированием контурных токов, протекающих через ту или иную ветвь. Контурный ток берется со знаком "плюс", если его направление совпадает с направлением тока ветви, и со знаком "минус" - при встречном направлении.

Метод наложения

Метод наложения основан на принципе суперпозиции, согласно которому ток в любой ветви сложной цепи равен алгебраической сумме частичных токов, вызываемых каждой из ЭДС цепи в отдельности. По методу наложения рассчитывают токи, возникающие от действия каждой из ЭДС, удаляя остальные ЭДС из цепи, но оставляя в схеме внутренние сопротивления источников. Затем находят токи в ветвях исходной цепи путем алгебраического сложения частичных токов.

П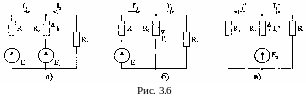 орядок выполнения расчета рассмотрим на примере цепи, показанной на рис. 3.6, а.

1. Определяют частичные токи I₁', I₂' и I₃' в ветвях электрической цепи при действии одной ЭДС E₁ (ЭДС Е₂ исключена из цепи) (рис. 3.6, б).

Направление частичных токов задают в соответствии с направлением ЭДС, расчет токов ведут с использованием метода эквивалентных преобразований.

2. Определяют частичные токи I₁", I₂" и I₃" при действии ЭДС Е₂ (рис. 3.6,в) (ЭДС E₁ исключена из цепи).

3. Определяют реальные токи I₁, I₂ и I₃ в ветвях исходной цепи (рис. 3.6, а) как алгебраическую сумму частичных токов при мысленном совмещении цепей, изображенных на рис. 3.6, б и 3.6, в.

Частичный ток берется со знаком "плюс", если его направление совпадает с направлением реального тока в исходной цепи, со знаком "минус" - при встречном направлении.

Метод двух узлов

Этот метод применяется для расчета электрических цепей с двумя узлами, между которыми включены активные и пассивные цепи (см. рис. 3.7).

Рис. 3.7

Положительные направления токов в ветвях выберем от узла а к узлу в. Вначале по формуле рассчитывается узловое напряжение U_ав, а затем по закону Ома рассчитываются токи в ветвях. Принимаем положительное направление напряжения U_ав от узла а к узлу в

U_ав= ,

где G₁, G_2, G_3, G₄- проводимости ветвей

G₁= ; G₂= ; G₃= ; G₄= .

Если ЭДС в ветви направлена навстречу узловому напряжению U_ав, то произведение EG записывается со знаком (+), если согласно – со знаком (-), независимо от положительных направлений токов. Если в ветви нет ЭДС, то произведение EG=0.

Токи в ветвях определяются по формулам:

I₁=(U_ав-E₁)G₁; I₂=U_авG₂= ;

; .

Рассмотрим вывод формулы для расчета тока I₃

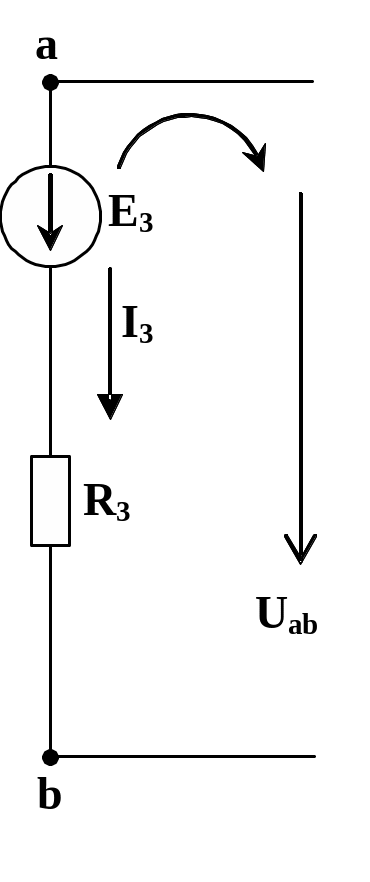
Рис. 3.8

Для изображенного контура составим уравнение по второму закону Кирхгофа

U_ав - R₃ I₃ = -E₃;

.

Баланс мощности электрической цепи

Баланс мощности цепи составляют для проверки правильности расчетов и записывают в виде

,

где Е_к, I_k и R_k –значения ЭДС источника, тока и сопротивления k – й ветви;

n – число ветвей, содержащих источники ЭДС;

m– число ветвей электрической цепи.

Баланс мощностей можно сформулировать так: сумма мощностей приемников равна сумме мощностей источников энергии.

В уравнении баланса произведение Е_kI_k (мощность источника) подстав- ляют со знаком "плюс", если истинное направление тока, протекающего через источник, и направление ЭДС источника совпадают, и со знаком "минус" – при встречном направлении (источник работает в режиме приемника).

Для электрической цепи, представленной на рис. 3.5, уравнение баланса мощностей будет иметь вид (при положительных значениях расчетных токов)

E₁I₁ – E₂I₂ = I₁²(R₁ + r₀₁) + I₂²R₂ + I₃²R₃ + I₄²R₄ + I₅²(R₅ + R₆).

Расчет потенциальной диаграммы

Потенциальной диаграммой называется график зависимости потенциала φ от сопротивления R, полученный при обходе контура.

Расчет потенциалов точек цепи выполняется после определения токов в ветвях одним из рассмотренных выше методов и нахождения истинных направлений токов.

Расчет рекомендуется производить в следующей последовательности.

1. Разбивают электрическую цепь (например, внешний контур) на участки, содержащие резисторы или источники ЭДС, обозначив буквами границы участков.

2. Потенциал одной из точек принимают равным нулю.

3. При обходе контура (направление произвольное) разность потенциалов φ_A – φ_B между концами каждого участка вычисляется по формулам, в зависимости от элемента, включенного на рассматриваемом участке цепи:

- если на участке включен резистор с сопротивлением R, то формула име- ет вид

При этом следует иметь в виду, что φ_A > φ_B, так как направление тока от большего потенциала к меньшему;

- если участок содержит источник ЭДС с внутренним сопротивлением R_вт, то возможны два случая:

- источник ЭДС работает в режиме источника питания (ток через источник совпадает с направлением ЭДС),

тогда разность потенциалов определяется по формуле _A - _B = E - R_вт I;

- источник ЭДС работает в режиме приемника (направления тока и ЭДС противоположны),

тогда формула примет вид _A - _B = E + R_вт I.

Расчетное значение потенциала точки, с которой начат обход контура, должно получиться равным нулю, что является критерием правильности расчета.

При построении потенциальной диаграммы по оси абсцисс в масштабе откладывают последовательно значения сопротивлений резисторов, включенных в контур; по оси ординат - значения потенциалов точек. Примерный вид потенциальной диаграммы изображен на рис. 3.9.

Рис. 3.9. Пример потенциальной диаграммы цепи