4. Характеристики форми розподілу
Аналіз закономірностей розподілу передбачає оцінювання ступеня однорідності сукупності, асиметрії та ексцесу розподілу.
Однорідність сукупності — передумова використання інших статистичних методів (середніх величин, регресійного аналізу тощо).
В однорідних сукупностях розподіли одновершинні (одномодальні). Багатовершинність свідчить про неоднорідний склад сукупності, про різнотиповість окремих складових. Критерієм однорідності сукупності вважається квадратичний коефіцієнт варіації,
З-поміж одновершинних розподілів є симетричні та асиметричні (скошені), гостро- та плосковершинні. У симетричному розподілі рівновіддалені від центра значення ознаки мають однакові частоти, в асиметричному — вершина розподілу зміщена. Напрям асиметрії протилежен напряму зсуву вершини. Якщо вершина зміщена вліво, то це правостороння асиметрія та навпаки.
В
симетричному розподілі характеристики
центру мають однакові значення х=Ме=Мо;
при правосторонній асиметрії
,
при лівобічній
.
Чим
більша асиметрія, тим більше відхилення
(
).
Очевидно, найпростішою мірою
асиметрії
є відносне відхилення
,
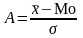яке характеризує напрям і міру скошеності
в середині розподілу; при правосторонній
асиметрії
,
при лівосторонній —
.
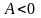Іншою властивістю одновершинних розподілів є ступінь зосередженості елементів сукупності навколо центра розподілу. Цю властивість називають ексцесом розподілу.
Асиметрія та ексцес — дві пов’язані з варіацією властивості форми розподілу. Комплексне їх оцінювання виконується на базі моментів розподілу.
Момент розподілу - це середня арифметична k-го ступеню відхилення (х-а). В загальному вигляді момент розподілу розраховується за формулою:
(5.7
а)
або
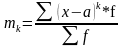(5.7
б)
де mk - момент k -го порядку,
х - варіанти ряду,
f - частоти ряду,
n - обсяг вибірки,
k та а - постійні числа.
Залежно від величини а моменти розділяють на початкові а=0, центральні а=х та умовні а=х0, де х0 - деяка варіанта ряду, звичайно близька до його середини. Ступінь k визначає порядок моменту.
Початковий момент k -го порядку виражається формулою:
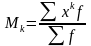(5.8)
Центральний момент k -го порядку виражається формулою:
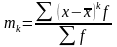(5.9)
Умовний момент k -го порядку виражається формулою:
(5.10)
Очевидно, що початковий момент 1-го порядку є середня арифметична, 2-го - середній квадрат значень ознаки. Центральний момент 2-го порядку характеризує дисперсію.
Центральни моменти 3-го і 4-го порядків характеризують відповідно асиметрію та ексцес. У симетричному розподілі m3=0. Чим більша скошеність ряду, тим більше значення величини. Для того щоб характеристика скошеності не залежала від масштабу вимірювання ознаки, для порівняння ступеня асиметрії різних розподілів використовується стандартизований момент Аs=m3/3, званий також коефіцієнтом асиметрії, який на відміну від коефіцієнта скошеності залежить від крайніх значень ознаки. При правосторонній асиметрії коефіцієнт Аs>0, при лівобічній Аs<0. Тому правосторонню асиметрію називають позитивною (додатною), а лівобічну – негативною (від'ємною). Вважається, що при Аs<0,25 асиметрія низька, якщо Аs не перевищує 0,5 - середня та при Аs>0,5 - висока.
Для вимірювання ексцесу використовують стандартизований момент 4-го порядку Е=m4/ 4. При симетричному, близькому до нормального розподілі Е=3, при гостровершинному розподілі Е>3, при плосковершинному Е<3.
Розрахунок центральних моментів m3 і m4 за даними інтервального ряду розподілу доцільно проводити за формулами:
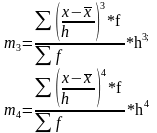(5.11)
де h - ширина інтервалу або будь-яке число,
f - частота або частість інтервалу.
Аналіз закономірностей розподілу можна поглибити, якщо описати його певною функцією.