1. В урне 3 белых и 8 черных шаров. Из урны вынимают сразу шесть шаров. Найти вероятность того, что три из них будут белыми.

2. Вероятности землетрясения в каждом из трех городов соответственно равны 0,2; 0,8 и 0,6. Найти вероятность того, что землетрясение произойдет только в двух городах.

3. Три стрелка произвели залп по цели. Вероятности поражения цели каждым стрелком соответственно равны 0,8, 0,9, 0,6. Найти вероятность того, что хотя бы один стрелок поразит цель.

4. На предприятии работают две бригады рабочих: первая производит ¾ продукции с процентом брака 5%, вторая - ¼ продукции с процентом брака 2%. Найти вероятность того, что наугад взятое не-бракованное изделие изготовлено второй бригадой.

5. Институт выпускает 80% специалистов высокого класса. Найти вероятность того, что среди 5000 выпущенных специалистов окажется 3700 высокого класса

6. Дискретная величина Х может принимать только два значения: х₁ и х₂, причем х₁ < х₂. Вероятность возможного значения х₁ равна 0,9, математическое ожидание М(Х) = 2,2 и дисперсия D(X) = 0,36. Составить закон распределения этой случайной величины.

7. Вычислить м(х), d(X), если задан ряд распределения случайной величины х:

Х	1	2	3	4	5
Р(Х)	??

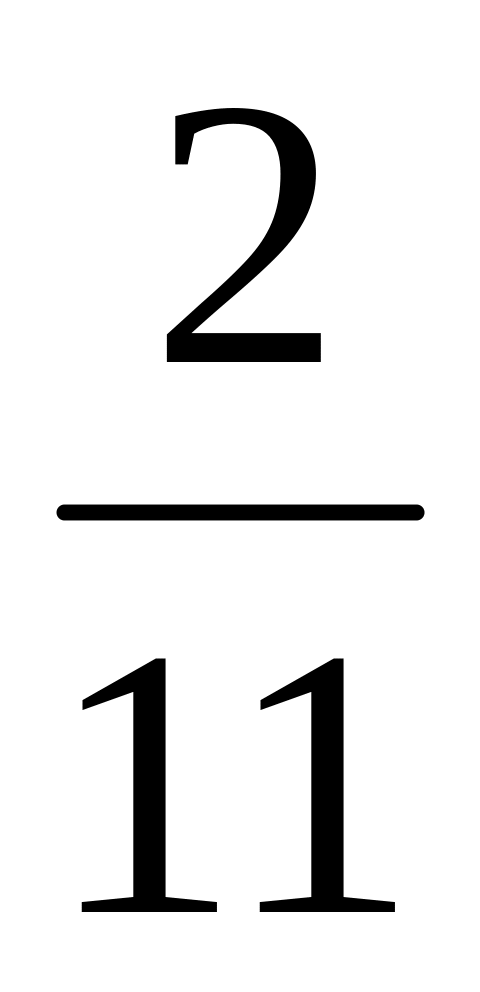
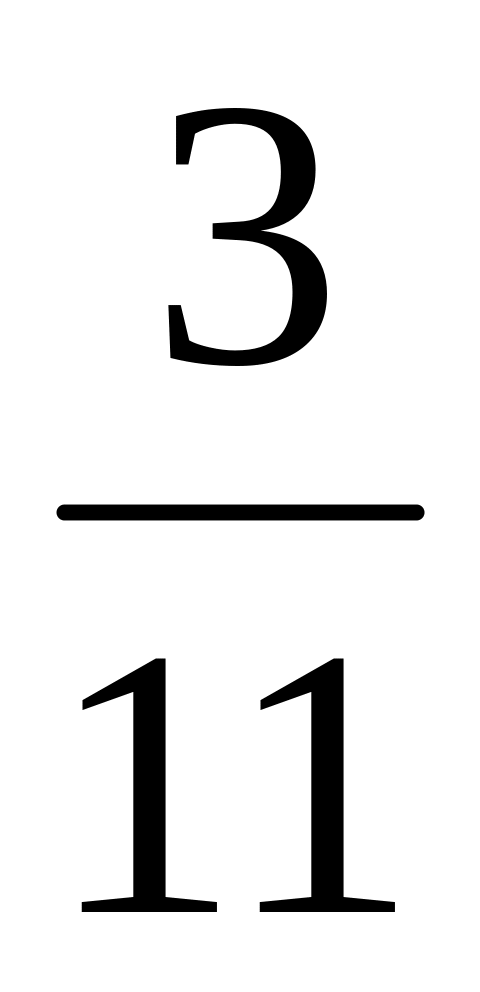
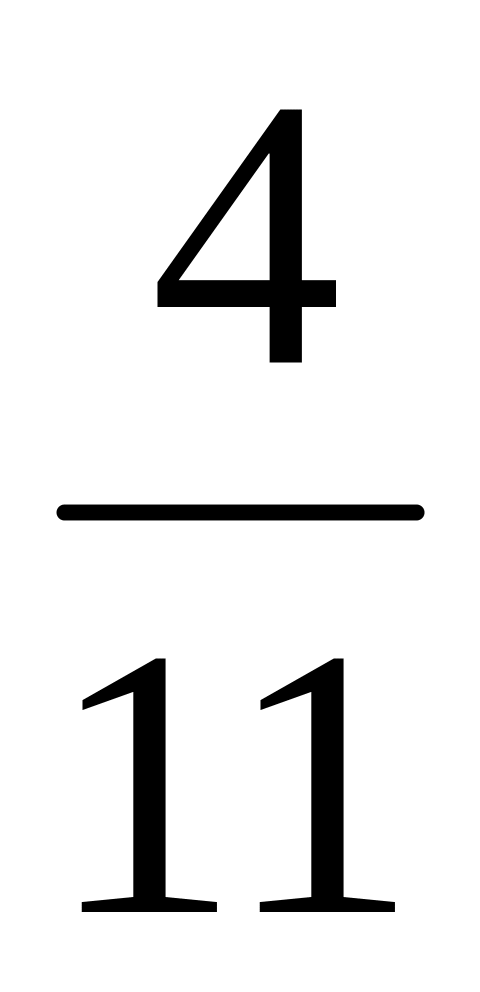
8. Вероятность попадания в цель из орудия при первом выстреле равна 0,7, при втором – 0,3, при третьем – 0,5. Найти закон распределения числа попаданий в цель, если произведено три выстрела.

9. Результаты наблюдений над величинами X и y приведены в следующей таблице:

X	-1	0	1	4
Y	0	1	2	5

Предполагая, что между X и Y имеется зависимость вида найти неизвестные коэффициенты a, b и c по методу наименьших квадратов. Вычислить Y при .

10. Данные об урожайности зерновых культур в некотором регионе получены с помощью собственно-случайной бесповторной выборки. Результаты обследования 100 предприятий из 1000 приведены в таблице:

Урожайность, ц/га	20– –30	30– –40	40– –50	50– –60	60– –70	70– –80	80– –90	90– –100	Итого:
Число предприятий	6	9	19	29	21	9	5	2	100

Используя -критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – урожайность зерновых культур – распределена равномерно.

Вариант №8