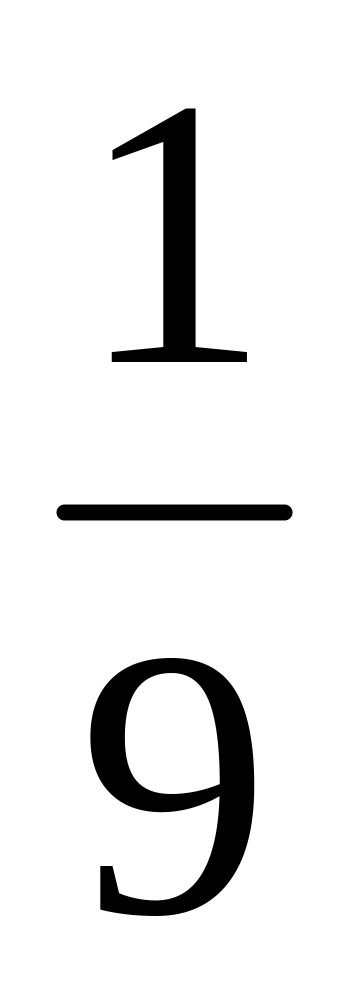- •Вариант №1
- •Вариант №2
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №3
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №4
- •Институт выпускает 90% специалистов высокого класса. Найти вероятность того, что среди 700 выпущенных специалистов окажется 20 невысокого класса.
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №5
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №6
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №7
- •Институт выпускает 80% специалистов высокого класса. Найти вероятность того, что среди 5000 выпущенных специалистов окажется 3700 высокого класса
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Вероятность попадания в цель из орудия при первом выстреле равна 0,7, при втором – 0,3, при третьем – 0,5. Найти закон распределения числа попаданий в цель, если произведено три выстрела.
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №8
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •В партии из 7 деталей имеется пять деталей первого сорта. Наудачу отобраны 4 детали для проверки. Найти закон распределения числа деталей первого сорта среди отобранных.
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №9
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №10
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №11
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №12
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №13
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №14
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №15
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №16
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №17
- •Вероятности землетрясения в каждом из трех городов соответственно равны 0,1; 0,8 и 0,6. Найти вероятность того, что землетрясение произойдет хотя бы в одном городе.
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №18
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №19
- •Вычислить м(х), d(X), если задан ряд распределения случайной величины х:
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
- •Вариант №20
- •Результаты наблюдений над величинами X и y приведены в следующей таблице:
Студент купил 4 лотерейных билета. Вероятность выигрыша по одному билету равна 0,3. Найти закон распределения числа выигрышей.
Результаты наблюдений над величинами X и y приведены в следующей таблице:
-
X
1
2
4
6
Y
2
2,5
2,3
2,1
Предполагая, что между X и Y имеется зависимость вида найти неизвестные коэффициенты a и b по методу наименьших квадратов. Вычислить Y при .
Распределение 80 предприятий, выпускающих однотипную продукцию, по количеству реализованных товаров X (тыс. ед.) и цене на производимые товары Y (тыс. руб. за ед. продукции) представлено в таблице:
y x |
10–20 |
20–30 |
30–40 |
40–50 |
50–60 |
Итого: |
60–70 |
|
|
|
3 |
3 |
6 |
70–80 |
|
|
1 |
5 |
4 |
10 |
80–90 |
|
2 |
7 |
7 |
1 |
17 |
90–00 |
|
6 |
10 |
4 |
|
20 |
100–110 |
2 |
7 |
8 |
2 |
|
19 |
110–120 |
4 |
4 |
|
|
|
8 |
Итого: |
6 |
19 |
26 |
21 |
8 |
80 |
Необходимо вычислить коэффициент корреляции и сделать вывод о тесноте и направлении связи между переменными X и Y.
Вариант №11
В ящике 11 деталей, 6 из которых стандартных. Из ящика вынимают сразу пять деталей. Найти вероятность того, что три из них будут стандартными.
Вероятности попадания в цель для каждого из трех орудий соответственно равны 0,9; 0,8 и 0,6. Найти вероятность того, что попадет в цель только два орудия.
Чему равна вероятность того, что при бросании трех игральных костей хотя бы на одной из них появится 6 очков?
Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы 4, из второй 6, из третьей – 5 студентов. Вероятность того, что студент первой, второй и третьей группы попадают в сборную института, соответственно равны 0,9, 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. Найти вероятность того, что студент из третьей группы.
Вероятность того, что расход электроэнергии за одни сутки не превысит нормы равна 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Дискретная величина Х может принимать только два значения: х1 и х2, причем х1 < х2. Вероятность возможного значения х1 равна 0,7, математическое ожидание М(Х) = 3,3 и дисперсия D(X) = 0,21. Составить закон распределения этой случайной величины.
Вычислить М(Х), (Х), если задан ряд распределения случайной величины Х:
-
Х
2
3
4
5
Р(Х)
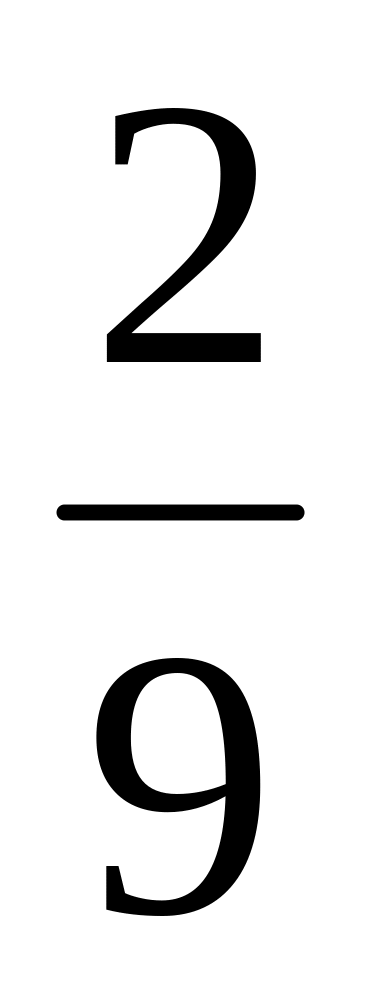
??