3. Порядок выполнения работы

Выполнение данной лабораторной работы включает в себя следующие этапы:

1. Изучение методики определения показателей надёжности по экспериментальным данным.

2. Сортировка выборки t_k,  по её возрастанию. Выборка в индивидуальном варианте читается слева направо и сверху вниз.

3. Определения интервалов t_i, .

4. Разработка и программирование алгоритмов определения значений r_i и r_i, и вычисления показателей надёжности по формулам (2), (4), (5), (7).

5. Программирование процедуры контроля правильности вычислений с использованием выражения (6).

6. Вывод результатов расчета осуществлять в виде таблицы:

Таблица 1

Номер интер-вала, i	Интервалы	Кол-во отказов	Интенсивность отказов	Плотность распреде- ления	Функция надёжности	Контроль
i	(ti,ti+1)	ri	*i	f*i	p*i	λ*ip*i- f*i=0

Средняя наработка на отказ Т* = … час.

7. Привести расчеты показателей надёжности для трех вариантов значений m (смотри индивидуальный вариант заданий).

4. Содержание отчета

1. Постановка задачи.

2. Формулы для расчета показателей надёжности.

3. Алгоритм или программа определения показателей надёжности.

4. Графики четырёх функций r_i(t_i), λ^*_i(t_i), f^*_i(t_i), p^*_i(t_i). На каждом графике по 3 кривых – для трёх вариантов величин m.

5. Выводы по работе:

• каково влияние величины m на значения показателей надёжности;

• дать заключение о виде закона распределения отказов изделий (равномерный, показательный или экспоненциальный).

Лабораторная работа №2 Расчет надёжности системы с независимыми элементами, работающими до первого отказа

1. Цели работы

1) Изучение методов расчета функции надёжности системы с учетом разнообразных связей ее элементов.

2) Получение навыков декомпозиции последовательно-параллельных структур анализируемых систем.

2. Методика расчета надёжности

Основной задачей теории надёжности является определение надёжности системы по надёжности составляющих ее элементов.

При расчете строится структура надёжности рассматриваемой системы с независимо работающими элементами, которая относится к одному из трех основных видов:

1. последовательное соединение;

2. параллельное соединение;

3. смешанное соединение элементов.

Пусть система состоит из n элементов, для которых заданными являются функции надёжности p_i(t) и отказа q_i(t),  . Требуется определить вид функции надёжности исследуемой системы p_C(t) и вычислить ее значения на интервале времени t[0,], а также определить среднее время безотказной работы.

Последовательное соединение элементов – это соединение, при котором отказ одного элемента приводит к отказу всей системы – приведено на рис.1:

Рис.1. Последовательное соединение элементов.

Функция надёжности такой системы вычисляется как:

pC(t)=p1(t)p2(t)…pn(t),

(8)

а функция отказа

qC(t)=1-[(1-q1(t))(1-q2(t))…(1-qn(t))].

(9)

Интенсивностью отказов λ(t) называют условную плотность вероятности возникновения отказа изделия при условии, что к моменту времени t отказ не возник:

(10)

где f(t) – плотность распределения отказов.

Интегрируя (10), легко получить:

(6)

Это выражение, называемое основным законом надёжности, позволяет установить временное изменение вероятности безотказной работы при любом характере изменения интенсивности отказов во времени. В частном случае постоянства интенсивности отказов λ(t)=const:

(11)

Полученный закон надёжности называется экспоненциальным и имеет большое значение в теории надёжности. Поток отказов при λ(t)=const называется простейшим, и именно он реализуется для большинства систем в течение периода нормальной эксплуатации от окончания приработки до начала старения и износа. Для каждого i-го элемента имеем, что

и   , ,

(12)

Подставив (12) в выражение (8), получим:

,

где _C - интенсивность отказов системы, которая вычисляется как

.

Среднее время безотказной работы такой системы будет равно:

TC=1/C.

(13)

Параллельное соединение элементов (см. рис.2) это такое соединение, при котором отказ системы возникает лишь при отказе всех её элементов. При этом функция отказов системы определяется как

qC(t)=q1(t)q2(t)…qn(t)

(14)

Функция надёжности такой системы будет равна:

pC(t)=1-[(1-p1(t))(1-p2(t))…(1-pn(t))].

(15)

Среднее время безотказной работы системы вычисляется по формуле:

.

(16)

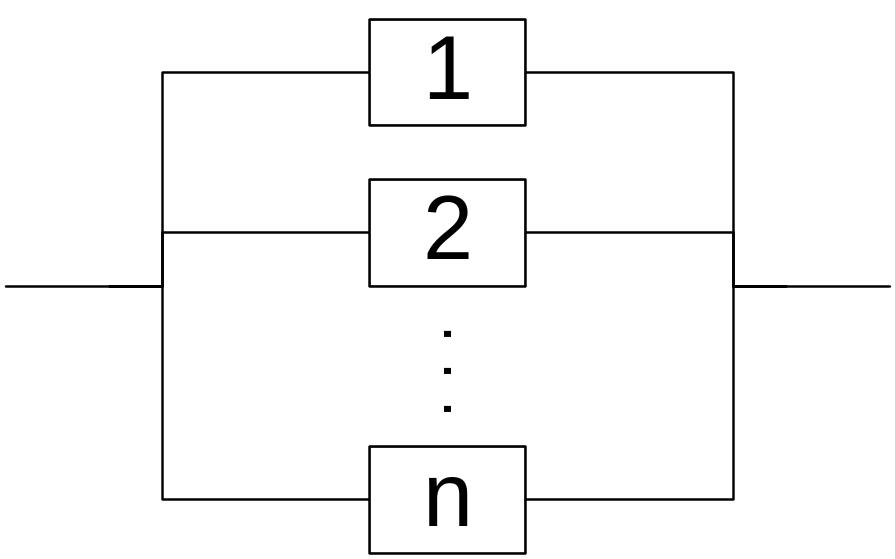
Рис.2. Параллельное соединение элементов.

Большинство реальных систем имеет сложную комбинированную структуру со смешанным соединением, часть элементов которой образует последовательное соединение, другая часть - параллельное, отдельные ветви структуры образуют мостиковые схемы (подробнее см. л.р.№4). В этих случаях целесообразно предварительно произвести декомпозицию системы, разбив ее на простые подсистемы - группы элементов, методика расчета надёжности которых известна (8), (9) и (14), (15). Затем эти подсистемы в структурной схеме надёжности заменяются квазиэлементами с вероятностями безотказной работы, равными вычисленным вероятностям безотказной работы этих подсистем.

Приведём пример расчета функций p_C(t) и q_C(t) для структуры системы приведенной на рис.3.

Разобьём систему на 3 подсистемы (блока) I, II, III. Блоки I и II соединены параллельно. Поэтому для них согласно (14) и (15) имеем, что:

qI,II=qIqII;  pI,II=1-(1-pI)(1-pII).

Здесь и ниже параметр время t опущен, а q_I, q_II, p_I, p_II означают соответствующие функции для блоков I и II. Эти блоки соединены с блоком III последовательно. Используя формулы (8), (9) имеем, что:

pC=pI,II,III=pI,IIpIII=[1-(1-pI)(1-pII)]pIII; qC=qI,II,III=1-pI,II,III=1-(1-qIqII)(1-qIII),

где p_III, q_III - показатели надёжности блока III.

Рис.3. Пример смешанного соединения (а) и его декомпозиция (б)

Для построения функций p_C(t) и q_C(t) требуется определить функции надёжности и отказов блоков I, II, III.

Блок I состоит из 6 элементов (в том числе элементов 1, 2 и подсистемы, состоящей из элементов 3, 4, 5 и 6). Эти элементы и выделенная подсистема соединены последовательным образом. Поэтому

pI=p1p2p3 4 5 6; qI=1-pI=1-(1-q1)(1-q2)(1-q3 4 5 6).

Элементы 3, 4, 5, 6 соединены параллельно. Следовательно

p3 4 5 6=1-(1-p3 4)(1-p5 6); q3 4 5 6=q34q56.

Элементы 3 и 4, а также 5 и 6 соединены последовательно, поэтому

p3 4=p3p4;   q3 4=1-(1-q3)(1-q4); p5 6=p5p6; q5 6=1-(1-q5)(1-q6)

Аналогичным образом для блока II запишем:

pII=p7p8 9 10 11p12; qII=1-(1-q7)(1-q8 9 10 11)(1-q12); p8 9 10 11=1-(1-p8 9)(1-p10 11); q8 9 10 11=q8 9q10 11;

p8 9=p8p9; q8 9=1-(1-q8)(1-q9); p10 11=p10p11;  q10 11=1-(1-q10)(1-q11)

Расчетные соотношения для блока III имеют вид:

pIII=P13P14; qIII=1-(1-q13)(1-q14).

Таким образом, если заданы функции надёжности p₁(t), p₂(t),…,p₁₄(t) и отказов q₁(t), q₂(t),…,q₁₄(t) каждого элемента, то можно вычислить надёжность всей системы.