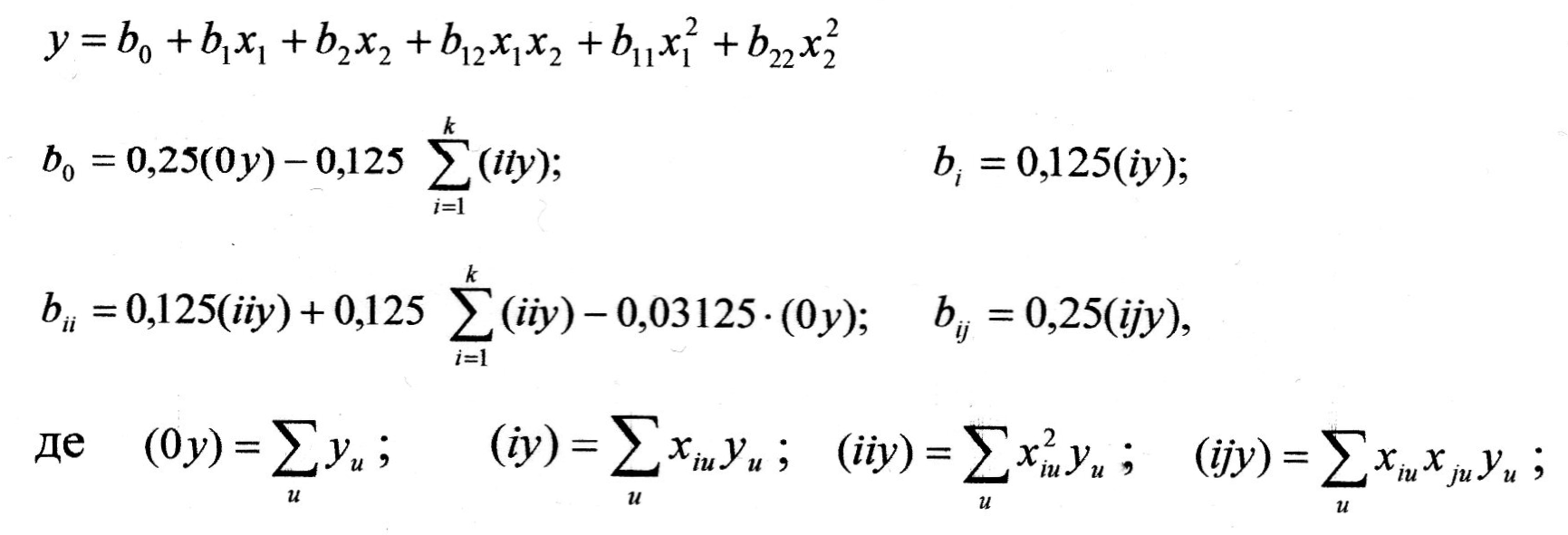- •Математичне моделювання, математичне планування і оптимізація багатофакторних експериментів та їх застосування у сучасних економічних дослідженнях.
- •Приклади отримання поверхонь відгуку, що геометрично відображають шукані аналітичні значення.
- •Розрахунок коефіцієнтів регресії багатофакторного поліномінального лінійного рівняння з допомогою методу найменших квадратів.
- •1. Однофакторне рівняння регресії.
- •2.Розглянемо загальний випадок: параметр уі; є функцією не тільки багатьох змінних, але і їх добутків - членів міжфакторної взаємодії.
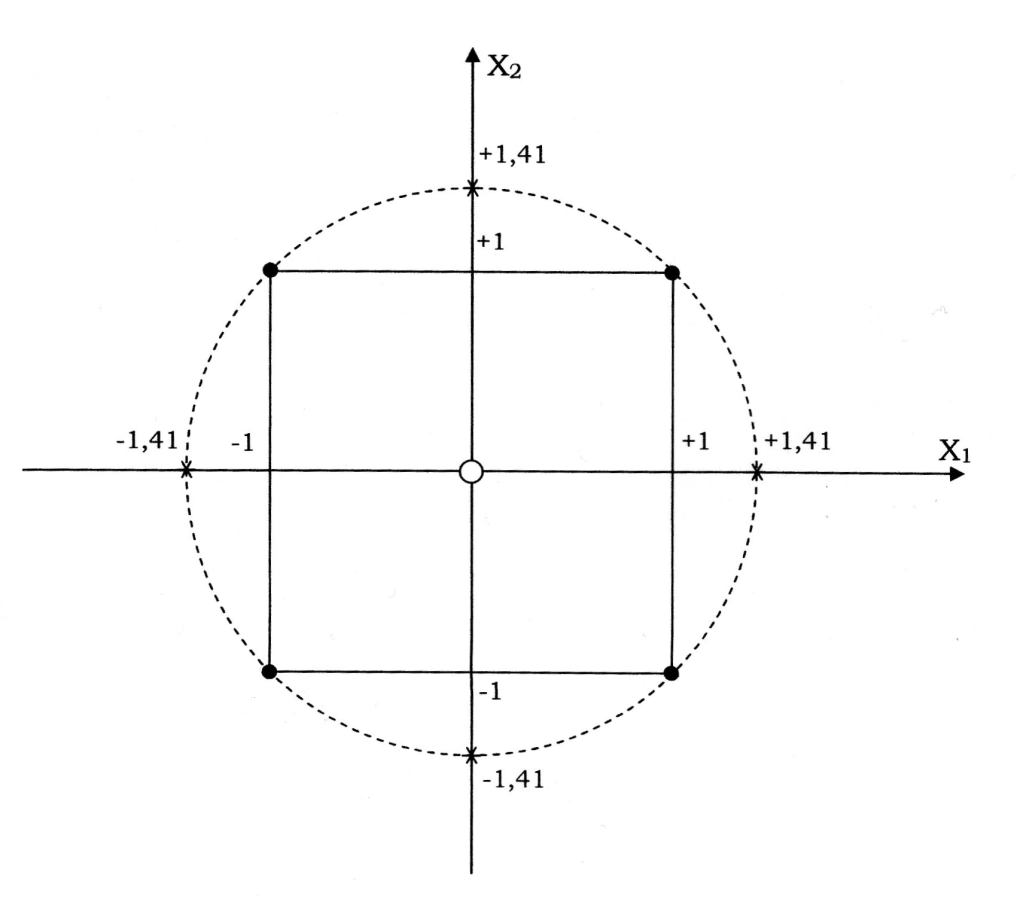
- •1. Просторова двохвимірна область планування для кодованих значень незалежних змінних у двохфакторному дослідженні.
- •2. Просторова трьохвимірна область планування для кодованих значень незалежних змінних у трьохфакторному дослідженні.
- •Похибки в дослідах та ефективність моделі
2.Розглянемо загальний випадок: параметр уі; є функцією не тільки багатьох змінних, але і їх добутків - членів міжфакторної взаємодії.
Оскільки b3,b4...розраховуються аналогічно до b1 і b2, а b13, b14, b23…,-аналогічно до b12, то достатньо розглянути розрахунок коефіцієнтів регресії у випадку двохфакторного регресійного поліномінального рівняння із змішаним членом міжфакторної взаємодії, а саме:
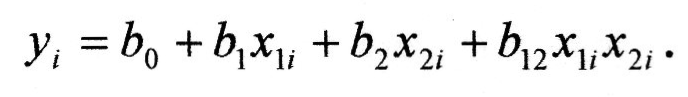
Запишемо
![]() і мінімізуємо суму квадратів
нев’язок
і мінімізуємо суму квадратів
нев’язок
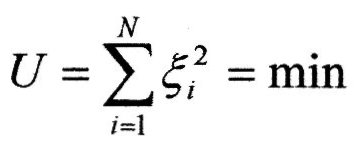 .
Мінімум функції досягається тоді, коли
.
Мінімум функції досягається тоді, коли
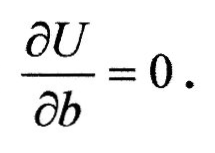
Розглянемо ці рівняння послідовно для b1, b2 і b12, враховуючи умови симетрії ( .7а), ( .7б):
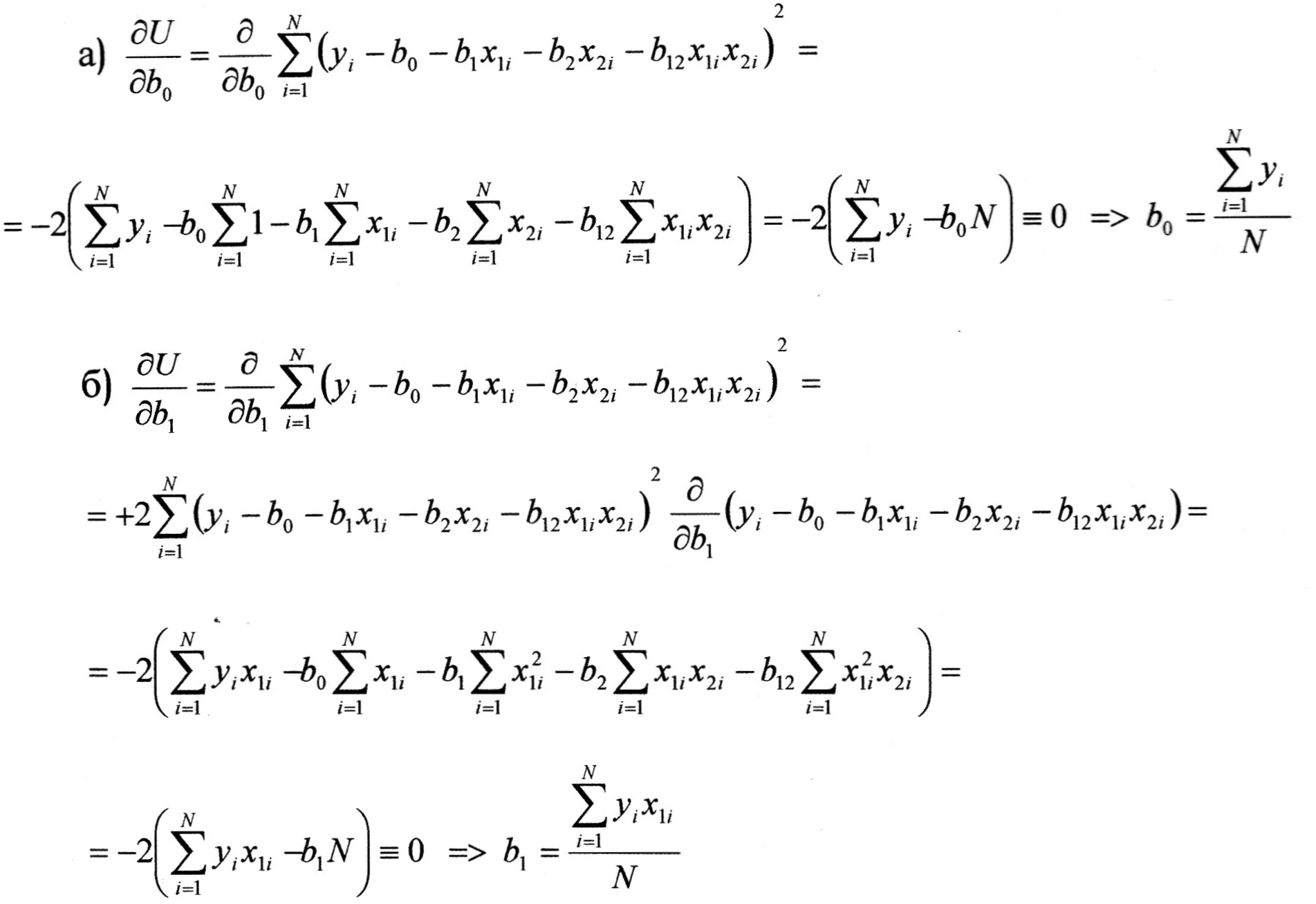
Аналогічно
для b2:
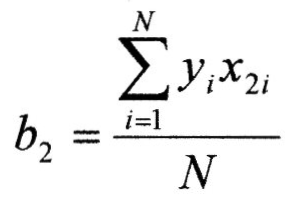
Тепер знайдемо коефіцієнт регресії міжфакторної взаємодії:
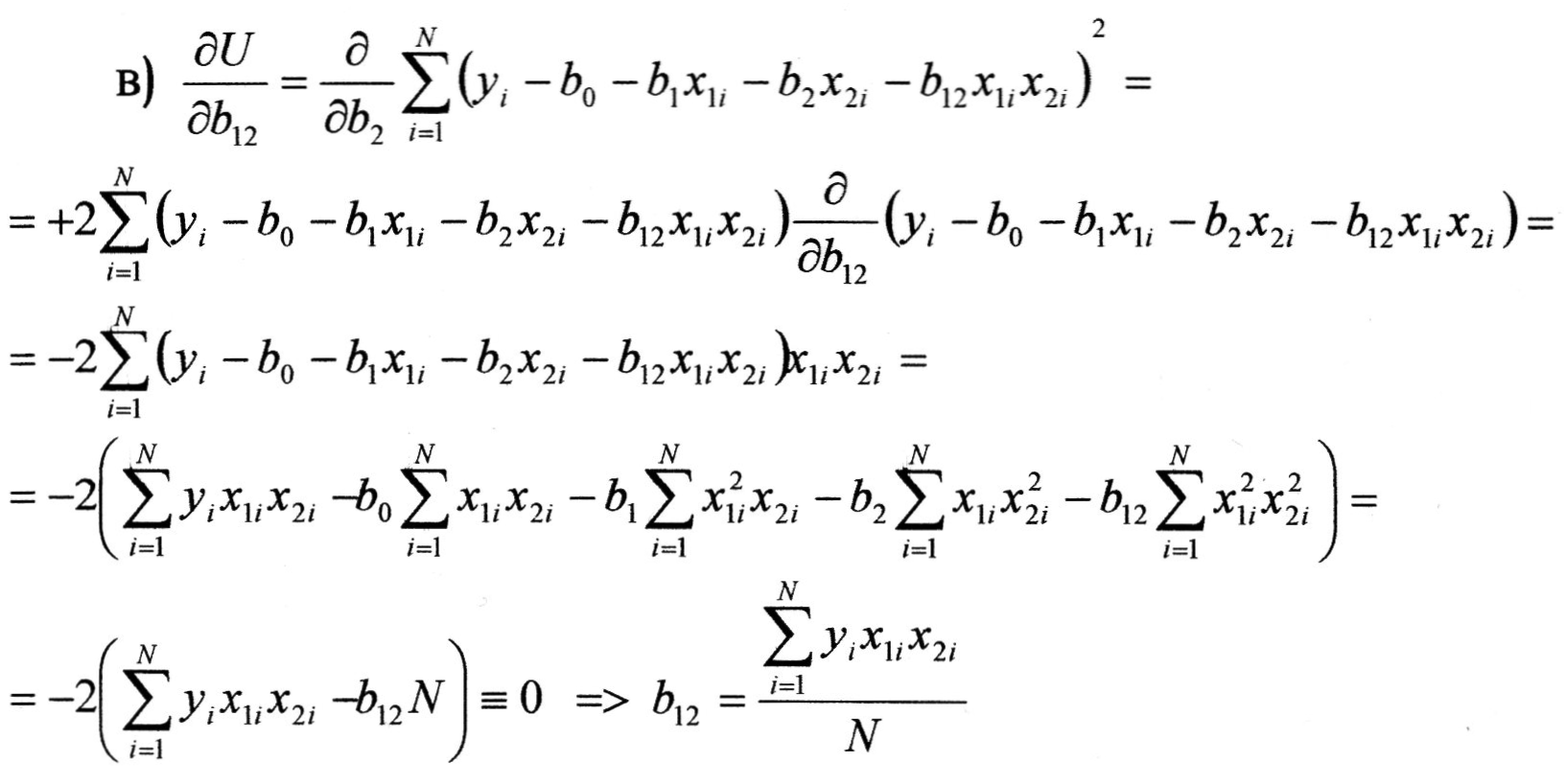
Остаточні результати:
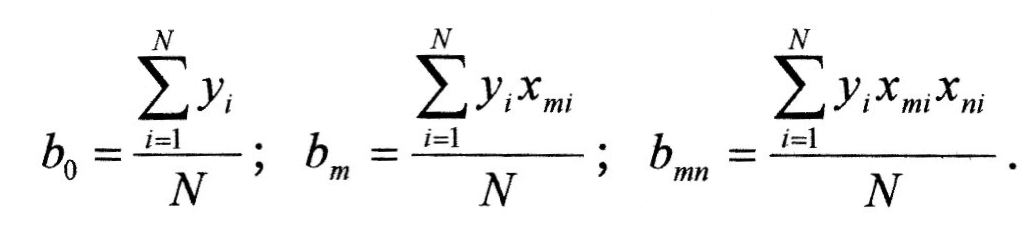
Загальний розрахунок формул для знаходження коефіцієнтів регресії багатофакторного поліномінального рівняння виду:

1. Просторова двохвимірна область планування для кодованих значень незалежних змінних у двохфакторному дослідженні.
Матриця планування для реалізації та проведення дослідів у випадку двох факторів для побудови поліномінального регресійного рівняння другого порядку.
Матриця планування для k=2 |
|||||||||
№ |
х0 |
х1 |
х2 |
х12 |
х22 |
х1 х2 |
уекс |
утр |
ξ2 |
1 |
1 |
-1 |
-1 |
1 |
1 |
1 |
уе1 |
ут1 |
(ут1- уе1)2 |
2 |
1 |
1 |
-1 |
1 |
1 |
-1 |
уе2 |
ут2 |
(ут2- уе2)2 |
3 |
1 |
-1 |
1 |
1 |
1 |
-1 |
уе3 |
ут3 |
(ут3- уе3)2 |
4 |
1 |
1 |
1 |
1 |
1 |
1 |
уе4 |
ут4 |
(ут4- уе4)2 |
5 |
1 |
-1,414 |
0 |
2 |
0 |
0 |
уе5 |
ут5 |
(ут5- уе5)2 |
6 |
1 |
1,414 |
0 |
2 |
0 |
0 |
уе6 |
ут6 |
(ут6- уе6)2 |
7 |
1 |
0 |
1,414 |
0 |
2 |
0 |
уе7 |
ут7 |
(ут7- уе7)2 |
8 |
1 |
0 |
-1,414 |
0 |
2 |
0 |
уе8 |
ут8 |
(ут8- уе8)2 |
9 |
1 |
0 |
0 |
0 |
0 |
0 |
уе9 |
ут9 |
(ут9- уе9)2 |
10 |
1 |
0 |
0 |
0 |
0 |
0 |
уе10 |
ут10 |
(ут10- уе10)2 |
11 |
1 |
0 |
0 |
0 |
0 |
0 |
уе11 |
ут11 |
(ут11- уе11)2 |
12 |
1 |
0 |
0 |
0 |
0 |
0 |
уе12 |
ут12 |
(ут12- уе12)2 |
13 |
1 |
0 |
0 |
0 |
0 |
0 |
уе13 |
ут13 |
(ут3- уе3)2 |
Σ |
13 |
0 |
0 |
8 |
8 |
0 |
Σ уекс |
Σ утр |
Σ(ут1- уе1)2 |
Розрахунок формул для знаходження коефіцієнтів регресії двохфакторного поліномінального рівняння другого порядку виду: