Математичне моделювання, математичне планування і оптимізація багатофакторних експериментів та їх застосування у сучасних економічних дослідженнях.

Використання математичних методів, а саме, побудова теорії планування експерименту — один з важливих шляхів підвищення ефективності не тільки природничих наукових досліджень, але і потужний засіб, що ефективно використовується в усіх сучасних економічних теоріях [ 1 -6].

Багатьох науковців із різних областей пізнання окрім зрозумілого бажання побудувати фундаментальну теорію на основі своїх досліджень, цікавлять і чисельні значення тих чи інших величин. Розбіжність у передбаченні даних, отримуваних з допомогою різних теорій, обумовлюють межі застосування цих теорій. Коли явища, які досліджуються, відбуваються в межах, що відповідають областям застосування кількох теорій одночасно, то здійснюється прорахунок величин досліджуваних параметрів з допомогою кожної з цих теорій, а потім порівнюються отримані результати з результатами відповідних дослідів.

Часто потрібно отримати чисельні результати без побудови фундаментальних теорій. Саме в цих випадках незамінною виявляється наука - статистика. В даний час статистичні методи використовуються у всіх областях людської діяльності і пізнання світу: у фізиці, математиці, хімії, біології, економіці, екології, політології. Але конкретні чисельні розробки таких методів започаткували англійські математики-статисти Бокс і Уілсон. Ці вчені, ніяким чином не бажаючи нехтувати чи ігнорувати важливість опису досліджуваних явищ з допомогою фундаментальних теорій, тим не менше при відсутності останніх або складності їх створення, старались отримувати і отримували необхідні чисельні результати з допомогою статистичних методів.

Для цього використовується так званий метод «чорного ящика», суть якого полягає в наступному. Як показує досвід в більшості випадків системи, що підлягають оптимізації, виявляються настільки складними, що не завжди піддаються теоретичному прорахунку. В таких випадках дослідження проводяться по принципу «чорного ящика»: будується аналітична залежність, що описує процес при неповному знанні всіх механізмів досліджуваного явища.

Таким чином, реальний об'єкт дослідження апроксимується кібернетичною системою, яку Нойберт Вінер назвав «чорним ящиком». Це і є суть кількісно-якісного підходу.

Уявімо собі дуже складну досліджувану систему, яка складається з безлічі елементів. /Для того, щоб дослідити її, нам необхідно знайти реакцію цієї системи на певні подразнення (механічні, оптичні, електромагнітні, хімічні і т. д.). Аналізуючи подальшу поведінку системи, тобто вивчаючи її «відгук» на ці «подразники», ми зможемо спершу припустити, а провівши додаткові дослідження потім і зрозуміти характер та структуру нашої досліджуваної системи.

У методі математичного планування експерименту ці «подразники», якими ми впливаємо на досліджувану систему, називаються факторами і позначаються х,- при умові, що число факторів змінюється від 1 до к, де к -число або кількість факторів.

Оскільки фактори - це змінні величини, які відповідають способам впливу зовнішнього середовища на об'єкт, що досліджується, то вони повинні задовільняти вимогам керованості та однозначності. «Відгуки» на вплив факторів, які визначають поведінку системи, що вивчається, в теорії планування експерименту (ТЕМПЕ) називаються параметрами оптимізації і позначаються у_і а їх кількість варіюється від у₁ і до у_m.

Дослідження систем з точки зору фундаментального аналізу означає знаходження математичної залежності між сукупністю параметрів У та сукупністю факторів X. Ця залежність шукатиметься у вигляді системи функціональних виразів наступного вигляду:

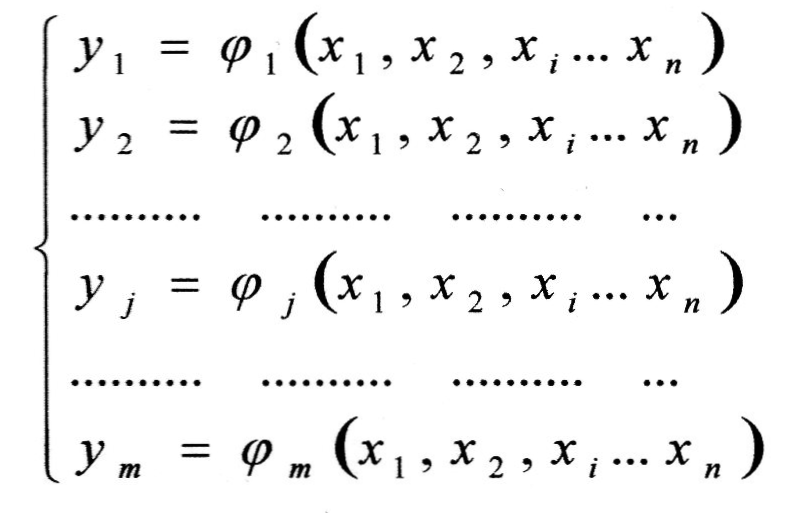
Очевидно, що на початкових етапах дослідження характер та вигляд цих функціональних залежностей нам не відомий.

Під час проведення дослідів вивчають залежність параметрів від багатьох факторів, які визначають як сам об'єкт дослідження, так і його стан. Оскільки реальна функція, що описує цю залежність, може бути досить складною, доцільно апроксимувати її більш простою, наприклад поліномом. У цьому випадку одержуємо математичну модель, яка дозволяє вибирати оптимальну стратегію дослідження навіть при неповному знанні всіх деталей процесу.

Математично задача формулюється так : необхідно одержати деяке представлення функції відгуку

де η — параметр процесу, x₁, x₂…..х_k - незалежні змінні фактори, які можна варіювати під час проведення експериментів. Координатний простір з координатами x₁, x₂, x₃…..х_k називається факторним простором, а геометричний образ, який відповідає функції відгуку — поверхнею відгуку.

Переважно дослідження поверхні відгуку проводять при неповному знанні механізму явищ, що вивчаються, і тому аналітичний вираз функції відгуку - невідомий. Тоді обмежуються поданням її поліномом

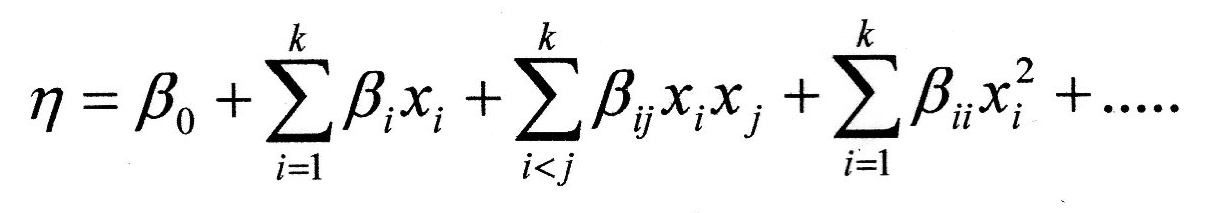
з коефіцієнтами регресії Розкладання функції в степеневий ряд еквівалентне апроксимацією її рядом Тейлора:

Користуючись результатами експерименту, можна визначити тільки вибіркові коефіцієнти регресії , які є оцінками для теоретичних коефіцієнтів . Запишемо рівняння регресії, одержане за результатами досліду

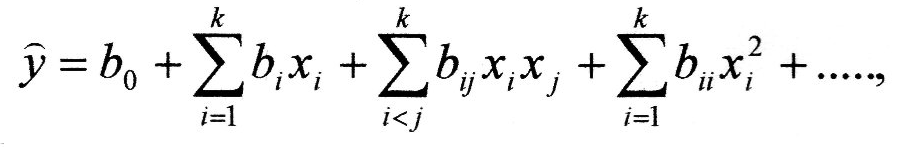
де — значення виходу, передбачене рівнянням.

Планування експерименту — це вибір кількості та умов проведення дослідів, необхідних і достатніх для апроксимації шуканої залежності певною математичною моделлю (функцією) з точністю, що вимагається. Якщо результати експериментів подати в матричній формі:

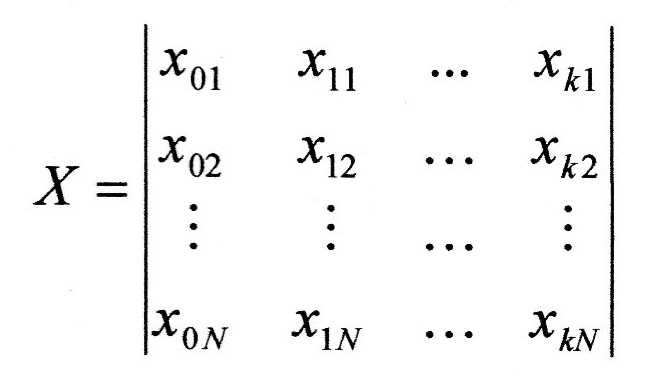
(де X - матриця незалежних змінних, У - матриця вектор-стовбець спостережень, к - кількість факторів, N - кількість дослідів), то матрицю-стовбець:

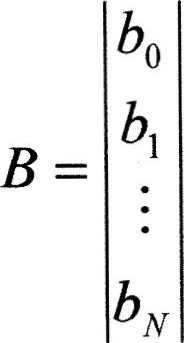
елементами в якій є коефіцієнти регресії можна знайти з системи нормальних рівнянь, які одержані з використанням методу найменших квадратів:

Від невизначеності, що пов'язана з неоднозначною кількісною оцінкою коефіцієнтів регресії, можна позбавитись, якщо експерименти планувати за деякою схемою, складеною так, щоб у матриці планування X скалярні добутки для всіх вектор-стовбців дорівнювали нулю. При такому ортогональному плануванні матриця коефіцієнтів нормальних рівнянь X* У стане діагональною і коефіцієнти регресії можна визначити незалежно один від одного. Наприклад, для двох факторів матриця планування першого порядку має вигляд:

Таблиця 1

Матриця планування першого порядку для двох факторів

Номер досліду	Матриця планування Х			Вектор виходу
№	х0	х1	х2	уі
1	+	-	-	у1
2	+	+	-	у2
3	+	-	+	у3
4	+	+	+	у4

Таблиця 2

Матриця планування першого порядку для трьох факторів

Номер досліду	Матриця планування Х					Вектор виходу
№	х0	х1	х2	х3	уі
1	+	-	-	-	у1
2	+	+	-	-	у2
3	+	-	+	-	у3
4	+	+	+	-	у4
5	+	-	-	+	у5
6	+	+	-	+	у6
7	+	-	+	+	у7
8	+	+	+	+	у8

де "-" вказує на те, що відповідний фактор приймає своє мінімальне значення, а "+" – максимальне. Перехід від натуральних до кодованих значень факторів здійснюється з допомогою перетворення:

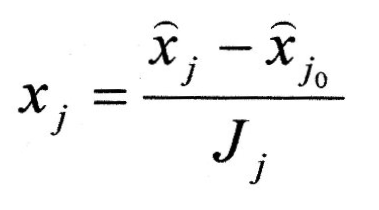
в якому: — кодоване значення фактору; — натуральне значення фактору; — натуральне значення основного (нульового між "-" і "+") рівня; J - інтервал варіювання фактору, j - номер фактору.

Оптимальним плануванням другого порядку рахують рототабельне планування, яке дозволяє одержувати симетричні інформаційні контури. В цьому випадку кореляційна матриця (X* X)^-1 інваріантна до ортогонального обертання координат.