2.5. Комплексное сопротивление и проводимость участка схемы

Рассмотрим пассивный двухполюсник (рис. 2.14):

Рис. 2.14

Комплексным сопротивлением Z пассивного участка схемы называется

отношение комплексного амплитудного (или действующего) значения напряже-

ния на полюсах этого участка к комплексному амплитудному (или действующему) значению тока на этом участке.

Введем обозначения:

Z = · = · ‾¹. (2.1)

Как любое комплексное число представим комплексное сопротивление в показательной и алгебраической формах:

Z = Z·е^jφ = ZCosφ + jZSinφ = R + jХ ,

где Z – модуль комплексного сопротивления участка схемы;

R – активное сопротивление или вещественная составляющая комплексного сопротивления;

Х – реактивное сопротивление или мнимая составляющая комплексного сопротивления.

Все сопротивления Z, Z, R, Х измеряются в Омах [Ом].

Исходя из уравнения (2.1), можно записать:

Z = )‾¹ = · · = U·I‾¹·е^jφ.

Модуль комплексного сопротивления , аргумент комплексного сопротивления φ = ψ_u – ψ_i, активная составляющая комплексного сопротивления R = Rе[Z], а реактивная составляющая Х = Im[Z]. На комплексной плоскости комплексное сопротивление Z может быть представлено вектором (рис. 2.15)

Рис. 2.15

Треугольник ОАВ на комплексной плоскости называется треугольником сопротивлений. Очевидны равенства:

φ = arctg .

Комплексной проводимостью участка цепи называется величина, обратная комплексному сопротивлению.

Введем обозначения.

Y – комплексная проводимость.

,

= I·U‾¹ = Z‾¹·e^–jφ = Y· e^–jφ ,

где Y – модуль комплексной проводимости.

Можно записать:

Y = g + jb,

где g = Rе [υ] – активная составляющая комплексной проводимости;

b = Im [Y] – реактивная составляющая комплексной проводимости.

Все проводимости Y, Y, g и b измеряются в Сименсах [Cм].

Связь между Y и Z определяется уравнениями:

Y = g + jb = – ,

следовательно:

; b = – .

Z = R + jХ = – ,

тогда:

Х = – .

2.6. Закон Ома в комплексной форме

Зная комплексное сопротивление (комплексную проводимость) участка схемы и напряжение, приложенное к данному участку, можно определить неизвестный ток:

.

Зная ток и комплексное сопротивление, можно найти комплексное действующее или комплексное амплитудное значения напряжения:

.

2.7. Реакция пассивных элементов на гармоническое воздействие

Активное сопротивление R

Пусть через сопротивление R идет ток i_R(t) = I_m·Sin (ωt+ψ_i), тогда

u_R(t) = R·I_m·Sin (ωt+ψ_i) = U_m·Sin (ωt+ψ_u), причем ψ_u = ψ_i , U_m = R·I_m.

Построим волновые диаграммы тока и напряжения на активном сопротивлении в одних координатах. Функции i_R(t) и u_R(t) совпадают по фазе, то есть их начальные фазы равны (рис. 2.16).

Рис. 2.16

Перейдем в частотную область или комплексную плоскость. Гармонической функции тока i_R(t) соответствует комплексное амплитудное значение тока:

i_R(t) → .

Аналогично гармонической функции напряжения u_R(t) соответствует комплексное амплитудное значение напряжения:

u_R(t) → .

По определению комплексное сопротивление Z_R активного сопротивления можно записать следующим образом:

.

Таким образом, комплексное сопротивление активного сопротивления не зависит от частоты.

Построим совмещенную векторную диаграмму (ВД) тока и напряжения на активном сопротивлении.

ВД – это совокупность векторов тока или напряжения на комплексной плоскости, характеризующая процессы в схеме в соответствии с законами Кирхгофа. Существует два типа ВД: лучевая и топографическая.

Лучевая ВД – это совокупность векторов (чаще всего тока), выходящих из одной точки на комплексной плоскости, например, три вектора выходят из начала координат (рис. 2.17):

Рис. 2.17

Каждый из векторов имеет свой модуль и аргумент.

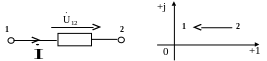Топографическая ВД – это замкнутая ломаная линия на комплексной плоскости, каждая сторона которой представляет собой вектор комплексного напряжения. На ВД стрелка вектора напряжения указывает более высокий потенциал в отличие от схем, где стрелка напряжения идет от более высокого потенциала (рис. 2.18).

Рис. 2.18

Лучевая ВД тока и напряжения активного сопротивления

Построим на комплексной плоскости вектор тока произвольной длины (модуль) и под любым углом к вещественной оси (начальная фаза). На этой же плоскости построим вектор напряжения длина которого тоже произвольна (рис. 2.19).

Рис. 2.19

Нельзя сравнивать длины векторов так как у них разная размерность.

Вектор напряжения совпадает по фазе (по направлению) с вектором , так как ψ_i = ψ_u. Разность начальных фаз φ_R = ψ_u – ψ_i = 0.

Обозначим φ разность фаз между векторами напряжения и тока в одном и том же элементе на участке цепи. Изобразим комплексное сопротивление Z_R и комплексную проводимость Y_R на комплексной плоскости (рис. 2.20):

Рис. 2.20

Индуктивность L

Полюсное уравнение индуктивности . Если через индуктивность проходит гармонический ток i_L(t) = Sin (ωt+ψ_i), то на ней будет гармоническое напряжение u_L(t) = = ωL Соs (ωt+ψ_i) =

= ωLSin (ωt+ψ_i + ) = Sin (ωt+ψ_u). Таким образом, ψ_u = ψ_i + ,

. Построим совмещенные временные (волновые) диаграммы тока i_L(t) и напряжения u_L(t) (рис. 2.21).

Рис. 2.21

Из диаграммы видно, что u_L(t) опережает по фазе i_L(t) на .

Перейдем в комплексную или частотную область.

i_L(t) → , u_L(t) → .

По определению комплексного сопротивления можно записать:

^-1 = ωL = ωL

или

= ωL = Х_L = jХ_L = jωL ,

где – комплексное сопротивление индуктивности;

Х_L = ωL – модуль комплексного сопротивления индуктивности.

Вектор напряжения на индуктивности опережает вектор тока индуктивности на . Разность фаз, то есть угол φ, на который вектор напряжения опережает вектор тока, составляет φ = .

Представим комплексное сопротивление и комплексную проводимость индуктивности на комплексной плоскости

.

Совмещенная ВД тока и напряжения на индуктивности, а также комплексные сопротивление и проводимость на комплексной плоскости имеют вид (рис. 2.22):

Рис. 2.22

Рассмотрим частотную зависимость сопротивления индуктивности.

Модуль Х_L комплексного сопротивления индуктивности может быть представлен в виде:

Х_L = ωL.

Следовательно, эта зависимость линейна. Представим ее в виде графика

( рис. 2.23):

Рис. 2.23

Нетрудно видеть, что зависимость Х_L(ω) – это прямая, проходящая через начало координат, причем с ростом индуктивности крутизна её (угол наклона к оси абсцисс) возрастает.

Рассмотри два крайних режима работы индуктивности:

1. Частота ω = 0. Это режим постоянного тока. Очевидно, что ω L=0, то есть в месте включения индуктивности будет коротко замкнутое соединение (рис.2.24). В этом случае

Рис. 2.24

2. Частота ω → ∞, в этом случае ωL → ∞, то есть в месте включения индуктивности будет разрыв (рис. 2.25):

Рис. 2.25

Емкость С

Если к емкости приложено гармоническое напряжение

u_C(t) = , то через неё идет гармонический ток i_C(t), определямый полюсным уравнением:

где ψ_i = ψ_u + ; .

Построим временные (волновые) диаграммы тока i_C(t) и напряжения u_C(t) на емкости (рис. 2.26):

Рис. 2.26

Напряжение u_С(t) на емкости отстает от тока i_С(t) емкости по фазе на угол .

Перейдем в комплексную, или частотную область.

i_С(t) → ,

u_L(t) → .

По определению комплексного сопротивления можно записать:

^-1 = (ωС)^–1 = (ωС)^–1 ,

= (ωС)^–1 = = –j(ωС)^–1 = –jХ_С ,

где - комплексное сопротивление емкости;

Х_С = (ωС)^–1 – модуль комплексного сопротивления емкости.

Вектор напряжения на емкости отстает от вектора тока емкости на угол .

Разность фаз, то есть угол φ между векторами напряжения на емкости и тока емкости составляет величину (– ), то есть φ = – .

Комплексная проводимость Y_С определится:

= jωC = jb_C .

Совмещенная ВД тока и напряжения на емкости, а также комплексное сопротивление и комплексная проводимость на комплексной плоскости имеют вид (рис. 2.27):

Рис. 2.27

Рассмотрим частотную зависимость сопротивления емкости.

Модуль Х_С комплексного сопротивления емкости может быть представлен в виде:

Х_С = (ωС)^–1,

следовательно эта зависимость гиперболическая. Представим ее в виде графика (рис. 2.28).

Рис. 2.28

Рассмотрим два крайних режима работы емкости.

1. Частота ω = 0. Х_С = (ωС)^–1 → ∞, то есть в месте включения емкости будет разрыв (рис. 2.29):

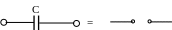
Рис. 2.29

2. Частота ω → ∞. Х_С = (ωС)^–1 → 0, то есть в месте включения емкости будет коротко замкнутое соединение (рис. 2.30):

Рис. 2.30