2.4. Представление гармонической функции на комплексной плоскости
Установившиеся значения токов и напряжений линейных схем при воздействии гармонических сигналов в принципе могут быть найдены путем составления и решения соответствующих этим процессам дифференциальных уравнений. Однако это достаточно сложный путь.
В конце ХIХ века американскими инженерами А. Кеннели и И. Штейнметцем был предложен более простой путь, основанный на представлении гармонических функций времени в виде комплексных чисел, то есть на переводе исходных функций из временной области в частотную.
Введем понятие
комплексных амплитудных значений
гармонических функций тока
(напряжения
,
э.д.с.
).
Представим для этого каждую из этих
функций в виде вектора на комплексной
плоскости, длина которого равна амплитуде
А m.
При этом он
вращается с круговой частотой ω против
часовой стрелки (рис. 2.13).
+1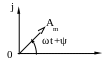
Рис. 2.13
Если остановить вектор в произвольный момент времени t, то его проекция а(t) на мнимую ось определится:
а(t) = Аm·Sin (ωt + ψ) .
При t = 0 а(0) = Аm·Sinψ.
Таким образом, гармонической функции а(t) = Аm·Sin (ωt + ψ) соответствует комплексное число Аm = Аmеjψ.
Аналогично гармоническим воздействиям
i(t) = Im·Sin (ωt + ψi), u(t) = Um·Sin (ωt + ψu) и е(t) = Еm·Sin (ωt + ψе)
соответствуют комплексные величины
,
и
,
представляющие собой вектора, вращающиеся в комплексной плоскости вокруг начала координат с частотой ω против часовой стрелки.
Пример 15. Дана гармоническая функция э.д.с. = 10·Sin (ωt + ) В. Нужно определить комплексное амплитудное значение э.д.с.
В.
Справедливо и обратное преобразование.
Дано комплексное
амплитудное значение тока:
А на частоте 100 рад/с. Нужно определить
гармоническую функцию тока вида:
i(t) = Im·Sin (ωt+ψi).
i(t)
= 0,5·Sin
(100t+
)
А.
Комплексное действующее значение тока или напряжения гармонической функции – это комплексное число, модуль которого равен действующему значению тока или напряжения, а аргумент равен начальной фазе гармонической функции.
Введем обозначения:
–
комплексное
действующее значение тока
‾1
·
;
– комплексное действующее значение напряжения
‾1
·
;
– комплексное
действующее значение э.д.с.
‾1
·
.
Пример 16.
Дана гармоническая функция напряжения
u(t)
= 10Sin(ωt
–
)
B.
Найти комплексное
амплитудное и комплексное действующее
зна-
чения напряжения.
В;
‾1
·
=
10 (
)‾1
·
= 7,07·
В.
Справедливо и обратное преобразование.
Известно комплексное действующее значение тока = 0,2еj70° А на частоте ω = 100 рад/с. Найти гармоническую функцию тока.
i(t) = Im·Sin (ωt+ψi) = I · ·Sin (ωt+ψi) = 0,2· ·Sin (100t+70°) =
=0,282·Sin(100t+70°) А.