1.7. Схемы замещения элементов эц

Реальный источник электрической энергии может быть представлен двумя схемами замещения: последовательным соединением источника э.д.с. и сопротивления или параллельным соединением источника тока и проводимости

( рис. 1.30):

Рис. 1.30

Здесь R_вн − внутреннее сопротивление источника э.д.с.,

g_i – проводимость источника тока.

Теперь рассмотрим схемы замещения пассивных реальных элементов.

Резистор – обычно высокоомный провод, пленка, порошок на изоляционном каркасе. Если пренебречь электрическим и магнитным полями в исследуемом диапазоне частот, то на постоянном токе и низкой частоте резистор можно моделировать сопротивлением (рис. 1.31,а), а на высоких частотах – сопротивлением, емкостью и индуктивностью (рис. 1.31,б):

а) б)

Рис. 1.31

Катушка индуктивности – определенное число витков проволоки на каркасе. Если ток и напряжение постоянны, то магнитное поле отсутствует, и учитывается только активное сопротивление R_К катушки( рис. 1.32,а). При переменном токе на низких частотах следует учитывать и индуктивность L_К катушки (рис. 1.32,б), а на частотах свыше 1 ГГц возникает ток смещения, поэтому следует учитывать и емкость С_К катушки (рис. 1.32,в):

R_К

R_К

L_К

R_К

L_К

ω = 0

С_К

а)

б)

в)

Рис. 1.32

Конденсатор – совокупность не менее двух проводников, разделенных прослойкой диэлектрика. Конденсатор на постоянном токе в схемах может быть представлен обрывом или сопротивлением (рис. 1.33,а). На низкой частоте конденсатор можно моделировать емкостью или емкостью и сопротивлением

(рис. 1.33,б), а на высоких частотах – соединением сопротивления, емкости и индуктивностью (рис. 1.33,в):

L

или или

в)

а)

б)

Рис. 1.33

2. Основы анализа схем с источниками гармонического сигнала

Задача анализа электрической схемы – определение реакции Y схемы на заданное внешнее воздействие Х, где Х и Y – функции времени t или угловой частоты ω. В частности, функции Х(t) и Y (t) могут быть токами или напряжением, а функции Х(ω) и Y (ω) могут быть частотными характеристиками какого –либо элемента. В общем случае как схемы, так и функции Х, Y могут быть многомерными.

Если функции Х и Y зависят от времени t, то анализ проводится во временной области, если они зависят от частоты ω, то анализ проводится в частотной области. Схематически внешние воздействия, исследуемая схема и её реакция на внешние воздействия могут быть отображены следующим образом (рис. 2.1):

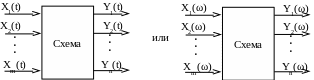
Рис. 2.1

2.1. Понятие о гармонических функциях

Функция а(t) называется гармонической, если она изменяется по синусои-дальному или косинусоидальному закону:

а(t) = А_mCos(ωt + φ) = А_msin( ωt + ψ).

Здесь аргумент υ(t) = ωt + ψ называется фазой. Величина ψ = φ + π/2, равная значению фазы при t = 0 , называется начальной фазой. Наибольшее значение функции – амплитуда А_m, наименьшее значение – (–А_m).

Фаза гармонической функции линейно увеличивается во времени. Скорость ω её изменения называется угловой частотой и измеряется в рад/с. Гармоническая функция – простейший вид периодической функции. Величина f, обратная периоду функции Т, называется линейной частотой и измеряется в герцах, обозначается Гц.

Установившимся режимом схемы называется такой, при котором закон изменения напряжения и тока не изменяется в течение всего исследуемого ин-

тервала времени. В противном случае режим является переходным.

Рассмотрим установившиеся процессы.

Построим график гармонической функции:

1. Выберем масштаб. По оси абсцисс – фазу ωt, чтобы определить период функции 2π. По оси ординат – амперы (если это функция тока) или вольты (если это функция напряжения). Отложим амплитуду функции А_m (рис. 2.2):

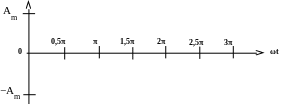
Рис. 2.2

2. Построим функцию а´(t) с начальной фазой ψ = 0 (рис.2.3):

Рис. 2.3

3. Сдвигаем построенную функцию по оси абсцисс на величину начальной фазы ψ. Если ψ > 0, то сдвигаем её влево, то есть функция а(ωt) опережает начало отсчета по оси абсцисс на величину ψ. Если ψ < 0, то сдвигаем вправо, то есть

функция а(ωt) отстает от начала отсчета на величину ψ.

Н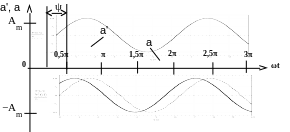 апример, при , получим (рис. 2.4):

Рис. 2.4

Пример 9. Построить график функции тока i(t) = 2 Sin(ωt + ) А.

1 . Выбираем масштаб по осям ординат (рис. 2.5).

Рис. 2.5

2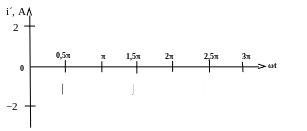 . Строим функцию i´(t) = 2 Sin(ωt +0) А (рис. 2.6).

Рис. 2.6

3. Сдвигаем построенную функцию по оси абсцисс на влево, так как

Ψ = > 0 (рис. 2.7):

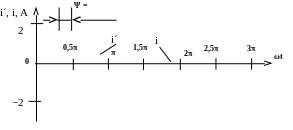
Рис. 2.7

Пример 10. Построить график функции напряжения u(t) = 10Sin(ωt – ) В.

1. Выбираем масштаб по осям ординат (рис. 2.8):

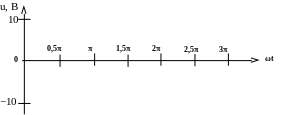
Рис. 2.8

2. Строим график функции u´(t) = 10 Sinωt В (рис. 2.9):

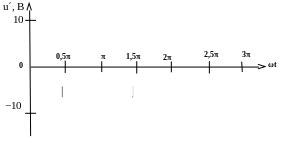
Рис. 2.9

3. Сдвигаем построенную функцию по оси абсцисс на вправо, так как

Ψ = – < 0 (рис. 2.10).

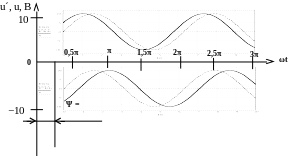
Рис. 2.10