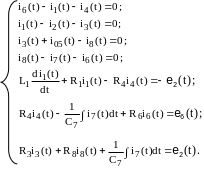1.6. Законы Кирхгофа – топологические уравнения

Математическое описание процессов в ЭЦ базируется на уравнениях двух типов – полюсных и топологических. Последние отражают свойства схемы, которые определяются только топологией и не зависят от того, какие элементы входят в состав ветвей.

Первый закон Кирхгофа устанавливает связь между токами ветвей в каждом из узлов схемы (ЭЦ) и формулируется так: алгебраическая сумма мгновенных значений токов всех ветвей, сходящихся в узел, равна нулю для любого момента времени:

Здесь N – число ветвей в рассматриваемом узле.

Правило знаков. Ток берется со знаком плюс, если он входит в узел, и со знаком минус, если он выходит из узла.

Перед составлением уравнений задаются направлениями токов в ветвях.

Число линейно независимых уравнений по 1-ому закону Кирхгофа на единицу меньше числа узлов. Если число уравнений равно Х_I, то справедливо равенство: Х_I = y – 1.

Пример 5. Задана схема (рис. 1.22).

Рис. 1.22

Зададимся направлением токов (произвольно). Число узлов y = 4. Число уравнений Х_I = y – 1 = 3. Выбираем три узла 1, 2 и 4.

К узлу 1 подключены три ветви: первая, четвертая и пятая. Первый i₁(t) и пятый i₀₅(t) токи выходят из узла, а четвертый i₄(t) – входит. Следовательно, в уравнение для узла "1" токи i₁(t) и i₀₅(t) войдут со знаком "–", а четвертый i₄(t) – со знаком "+".

–i₁(t) + i₄(t) – i₀₅(t) = 0.

К узлу "2" подключены три ветви: первая, вторая и третья. Ток i₁(t) входит в узел, а токи i₂(t) и i₃(t) – выходят из узла. Следовательно, в уравнение для узла "2" ток i₁(t) войдет со знаком "+", а токи i₂(t) и i₃(t) – со знаком минус.

i₁(t) – i₂(t) – i₃(t) = 0.

Аналогично составляем уравнение для узла "4".

i ₂(t) + i₀₅(t) – i₄(t) – i₆(t) – i₇(t) = 0.

Второй закон Кирхгофа устанавливает связь между напряжениями на участках схемы, входящих в произвольный контур, и формулируется так: алгебраическая сумма мгновенных значений напряжений, входящих в замкнутый контур, в любой момент времени равна нулю:

.

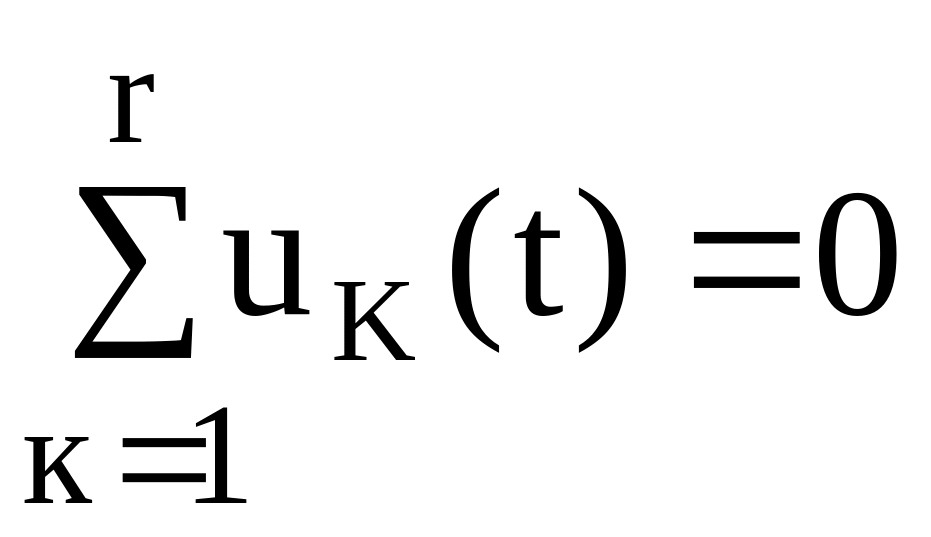Здесь r – число элементов, входящих в контур.

Учитывая, что положительное направление напряжения источника э.д.с. противоположно направлению э.д.с., закон можно записать в виде

.

Здесь r_е – число источников э.д.с., входящих в контур.

Закон можно сформулировать так: алгебраическая сумма мгновенных значений напряжений на пассивных элементах в замкнутом контуре равна алгебраической сумме э.д.с., входящих в этот контур, для любого момента времени.

Правило знаков: напряжение или э.д.с. берутся со знаком плюс если их направление совпадает с выбранным направлением обхода контура, и со зна-

ком минус, если не совпадает. Нужно помнить, что положительное направление напряжения на пассивном элементе (R, L, C) совпадает с направлением тока, поэтому напряжение на пассивном элементе берется со знаком плюс, если направление обхода контура совпадает с направлением тока в этом элементе.

Пример 6. Задана схема (рис. 1.23).

Рис. 1.23

Задаемся произвольно направлением токов i₁(t), i₂(t), i₃(t) и i₄(t). Выбираем

произвольно направление обхода контура – по часовой стрелке.

Уравнение по II закону Кирхгофа примет вид:

– – ℮₁(t) – ℮₄(t).

Слагаемые взяты со знаком минус, так как ток i₃(t) направлен навстречу направлению обхода контура. Аналогично э.д.с. ℮₄(t) взята со знаком минус.

Уравнения по II закону Кирхгофа числом Х_II чаще всего входят в систему уравнений для определения токов ветвей.

Если число ветвей обозначено в, а число ветвей с источниками токов в_i, то очевидно, что число Х неизвестных токов, а следовательно и число уравнений всей системы по законам Кирхгофа определится:

Х = в – в_i = Х_I + Х_II

Таким образом, Х = Х_I + Х_II, но Х_I = y – 1, поэтому

Х_II = в – в_i – (y – 1) = в – в_i – y + 1.

Кроме приведенной формулы расчета числа уравнений по II закону Кирхгофа существует связь между независимыми контурами схемы, главными ветвями и числом уравнений Х_II.

Число Х_II уравнений в системе определения токов ветвей равно числу главных ветвей и равно числу независимых контуров.

Алгоритм составления систем уравнений по законам Кирхгофа для определения токов ветвей состоит в следующем.

1. Обозначают узлы и строят дерево, а затем граф схемы, по которому определяют число независимых контуров.

2. Выбирают независимые контуры и задаются направлением их обхода.

3. Определяют число Х_I уравнений по формуле:

Х_I = y – 1.

4. Задаются направлением токов ветвей, не содержащих источников тока (произвольно).

5. Составляют систему из Х_I уравнений по I закону Кирхгофа.

6. Определяют число Х_II уравнений, равное числу независимых контуров.

7. Составляют Х_II уравнений для независимых контуров схемы.

8. Выражают напряжения на пассивных элементах через их токи с помощью полюсных уравнений.

Пример 7. Задана схема (рис. 1.24).

Рис. 1.24

Требуется составить систему уравнений относительно токов ветвей во временной области на основании законов Кирхгофа.

1. Строим дерево и граф схемы (рис. 1.25):

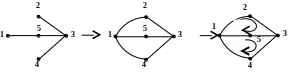
Рис. 1.25

Ветви 2 и 7 содержат источники тока, имеющие бесконечно большое сопротивление, поэтому на дереве и графе они не изображаются.

Из графа следует, что главных ветвей две. Следовательно два независимых контура и два уравнения по II закону Кирхгофа. Х_II = 2.

2. Задаемся направлениями обхода контуров по часовой стрелке.

3. Определяем Х_I = y – 1 = 5 – 1 = 4.

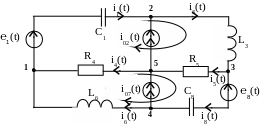4. Задаемся направлением тока ветвей, не содержащих источников тока (рис. 1.26).

Рис. 1.26

5. Записываем уравнения по I закону Кирхгофа:

для узла 1: i₄(t) – i₁(t) + i₆(t) = 0;

для узла 2: i₁(t) + i₀₂(t) – i₃(t) = 0;

для узла 3: i₃(t) – i₅(t) – i₈(t) = 0;

для узла 4: i₈(t) – i₆(t) – i₀₇(t) = 0.

6. Записываем уравнения по II закону Кирхгофа.

Для верхнего контура (ветви первая, третья, пятая и четвертая):

= ℮₁(t).

Для нижнего контура (ветви четвертая, пятая, восьмая, шестая)

– – = – ℮₈(t).

7. Выражаем напряжения на элементах через токи:

= ℮₁(t);

= – ℮₈(t).

8. Записываем полную систему уравнений:

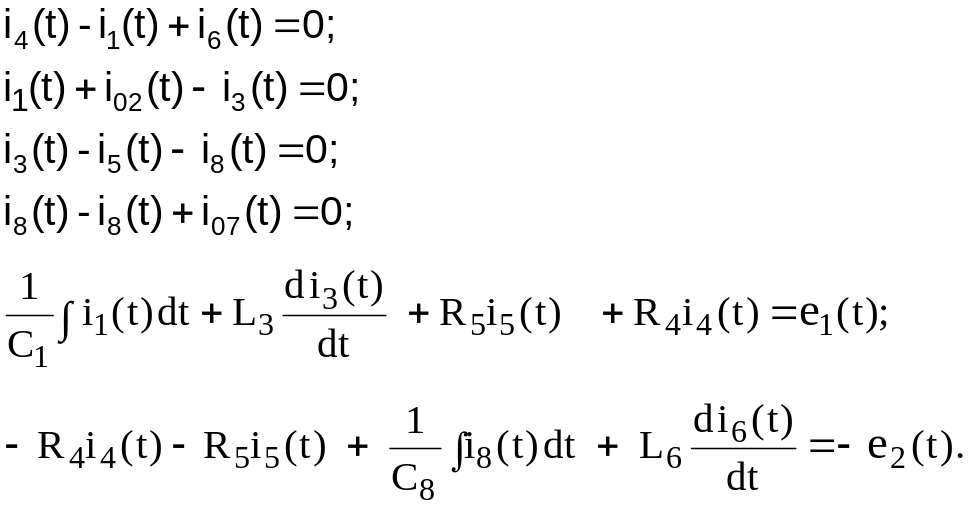
П ример 8. Задана схема (рис. 1.27).

Рис. 1.27

Требуется составить систему уравнений Кирхгофа.

1. Строим дерево и граф схемы (рис. 1.28):

Рис. 1.28

Ветвь 5 содержит источник тока, имеющий бесконечно большое сопротивление, поэтому на дереве и графе она не изображается.

Из графа следует, что главных ветвей три, следовательно три независимых контура и три уравнения по II закону Кирхгофа. Х_II = 3.

2. Задаемся направлением обхода независимых контуров по часовой стрелке.

3. Определяем Х_I = y – 1 = 5 – 1 = 4.

4. Задаемся направлением тока ветвей, не содержащих источников тока (рис. 1.29):

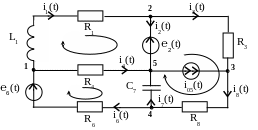
Рис. 1.29

5. Записываем уравнения по I закону Кирхгофа:

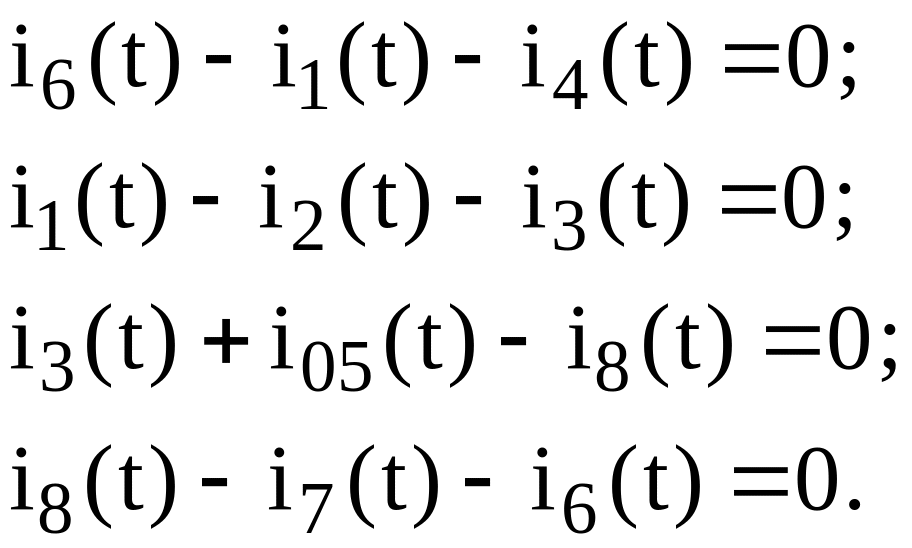
6. Записываем уравнения по II закону Кирхгофа

– = – ℮₂(t);

– ℮₆(t);

= ℮₂(t).

7. Выражаем напряжения на элементах через токи:

8. Записываем полную систему уравнений: