1.5. Основы топологии электрических схем

Полюсами электрических схем называются внешние выводы схем или их участков. По числу полюсов схемы делят на двухполюсники и многополюсники. Например, схему (рис. 1.16)

Рис. 1.16

можно представить двухполюсником относительно полюсов (точек) 1 – 2. Данный двухполюсник является пассивным, так как он содержит только пассивные элементы.

Двухполюсник является активным, если он содержит источники энергии. Например (рис. 1.17):

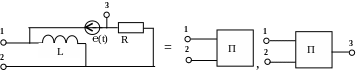
Рис. 1.17

Если эту схему рассматривать относительно полюсов 1 – 2, то она представляет собой активный двухполюсник, если же относительно полюсов 1,2,3 – активный трехполюсник.

Ветвь – участок схемы, по которому идет один и тот же ток.

Узел – место соединения трех или более ветвей.

Контур – замкнутая линия, проходящая по отдельным ветвям схемы. Характеризуется направлением обхода, выбираемым произвольно: по или против часовой стрелки.

Дерево схемы – совокупность отрезков прямых, соединяющих все узлы схемы, но не образующих замкнутых контуров. Ветви с источниками тока в дерево не входят.

Граф схемы – это её дерево, дополненное недостающими ветвями, называемыми хордами или главными ветвями. Ветви с источниками тока в граф схемы не входят.

Теория графов – это отдельный раздел математики, достаточно подробно изложенный в литературе .

При топологическом исследовании схем их ветви заменяют отрезками, соединяющими узлы. При этом источники энергии заменятся их внутренними сопротивлениями, а именно источники э.д.с. – коротко замкнутыми соединениями, а источники тока – обрывами.

Рассмотрим приведенные топологические понятия на примере.

П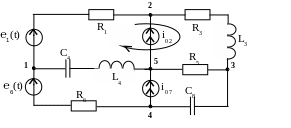 ример 4.

Рис. 1.18

Схема (рис. 1.18) включает 8 ветвей. Обозначим в = 8. Обычно в схемах индексы элементов соответствуют номеру ветви, в которую они включены. Так, в 1-ю ветвь включены источник ℮₁(t) э.д.с. и активное сопротивление R₁. По ЕСКД индексы пассивных элементов в схемах такой же высоты, как и символ элемента, однако в расчетах индекс должен быть значительно меньше, иначе он читается как множитель.

Схема включает 5 узлов, обозначенных цифрами 1 – 5. Обозначим число узлов y = 5.

Чтобы построить дерево, необходимо вынести узлы, а затем соединить их прямыми линиями так, чтобы не идти через ветви с источниками тока и не образовывать замкнутых фигур, например (рис. 1.19):

Рис. 1.19

Для одной схемы можно построить несколько деревьев. Например, для схемы , приведенной на рис. 1.18, можно построить еще два дерева (рис. 1.20):

Рис. 1.20

Если теперь любое из деревьев дополнить недостающими ветвями (хордами), за исключением ветвей с источниками тока, то получим граф схемы

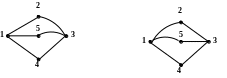( рис. 1.21):

Рис. 1.21

Хорды (главные ветви) изображают дугами.

В первом графе главные ветви третья и пятая, во втором – первая и четвертая.

Число главных ветвей не зависит от способа построения графа и определяется только схемой. В данной схеме их две.

Контур, например, может проходить по ветвям первой, третьей, пятой и четвертой. Зададимся в этом контуре направлением обхода по часовой стрелке.