6. Метод наложения

Метод наложения, используемый для расчета сложных линейных ЭЦ, основан на принципе наложения или суперпозиции.

Суть этого принципа заключается в том, что реакция Y(t) линейной ЭЦ на сложное воздействие , представляющее собой линейную комбинацию n более простых воздействий равна линейной комбинации реакций , вызванных каждым из n простых воздействий в отдельности: .

Под воздействиями и реакциями в ЭЦ подразумеваются токи и напряжения.

Рассмотрим принцип наложения в применении к расчету токов или напряжений в сложных линейных схемах.

Ток любой ветви определяется как алгебраическая сумма частичных токов для каждого из n источников э.д.с., включенных в схеме.

Метод наложения – это метод расчета токов и напряжений в сложной линейной схеме, основанный на определении частичных токов и напряжений от каждого источника энергии.

Ток (или напряжение) любой ветви линейной схемы равен алгебраической сумме частичных токов (или напряжений) от каждого источника энергии.

Частичным током называется ток от одного источника, определенный в предположении, что остальные источники замещены их внутренними сопротивлениями (источник э.д.с. – коротко замкнутое соединение, источник тока – обрыв).

Правило знаков

Частичный ток берется со знаком плюс, если его направление совпадает с выбранным направлением полного тока в исходной схеме, и берется со знаком минус, если не совпадает. В схеме частичный ток ℓ-ой ветви, вызванный k-м ис-

точником, будем обозначать .

Алгоритм расчета токов методом наложения

1. Задаемся направлением искомого тока (напряжения) в исходной схеме.

2. Переходим к частичным схемам для каждого источника энергии, заменяя остальные источники их внутренними сопротивлениями. Число частичных схем равно числу источников.

3. Определяем частичные токи в каждой из частичных схем.

4. находим полный искомый ток (напряжение) как алгебраическую сумму частичных токов.

Пример 50. Определить методом наложения ток второй ветви в следую- щей схеме (рис. 6.1) с известными параметрами.

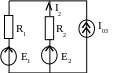
Задаемся направлением тока I₂.

Формируем три частичных схемы (рис. 6.2):

Рис. 6.1

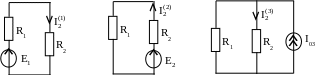
Рис. 6.2

Определяем частичные токи в каждой из частичных схем:

.

Полный ток определится:

.

Метод наложения справедлив только для токов и напряжений. Он неприемлем, например, для мощностей, так как мощность является не линейной, а квадратичной функцией тока и напряжения.

Так, мощность Р, выделяемая в сопротивлении R₂ ,

не равна сумме мощностей от частичных токов:

.

7. Теорема взаимности

В линейной схеме ток k-ой ветви , вызванный э.д.с. j-ой ветви , равен току j-ой ветви , вызванному э.д.с. k-ой ветви , если :

, если .

Ток j-ой ветви связан с э.д.с. взаимным сопротивлением :

.

Если в схеме с единственным источником э.д.с. известно взаимное сопротивление, то можно найти ток , и наоборот.

в схеме с единственным источником э.д.с. при известном токе j-ой ветви для определения взаимного сопротивления j-ой ветви и ветви с источником э.д.с. необходимо разделить комплексное действующее значение э.д.с. на комплексное действующее значение тока j-ой ветви:

.

П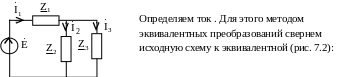 ример 51. Определить взаимные сопротивления для следующей схемы (рис. 7.1):

Рис. 7.1

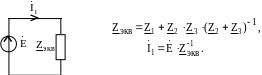
Рис. 7.2

.

.

По аналогии для взаимного сопротивления :

.

Взаимное сопротивление между ветвью с источником и ветвью, в которой определяется ток, равно сопротивлению ветви с источником плюс сопротивление ветви, в которой определяется ток, плюс произведение этих сопротивлений, деленное на сопротивление третьей ветви.

Эта формула справедлива для схемы из трех ветвей с одним источником. Она позволяет определить токи в схеме из трех ветвей наиболее быстрым способом.

Пример 52. Определить токи в ветвях схемы (рис. 7.3), используя взаимные сопротивления в схеме с известными параметрами.

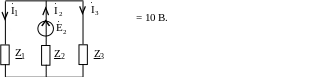
Рис. 7.3

Выбираем направления токов в ветвях схемы.

Определяем взаимные сопротивления :

Определяем токи :

А.

Определяем ток , используя I закон Кирхгофа:

или