
- •1. Основные понятия и законы
- •1.1. Электрическая цепь
- •1.2. Электрический ток и напряжение
- •1.3. Мгновенная мощность и энергия
- •1.4. Электрические схемы замещения
- •1.5. Основы топологии электрических схем
- •1.6. Законы Кирхгофа – топологические уравнения
- •1.7. Схемы замещения элементов эц
- •2. Основы анализа схем с источниками гармонического сигнала
- •2.1. Понятие о гармонических функциях
- •2.2. Среднее и действующее значения гармонических токов и
- •2.3. Операции с комплексными числами
- •2.4. Представление гармонической функции на комплексной плоскости
- •2.5. Комплексное сопротивление и проводимость участка схемы
- •2.6. Закон Ома в комплексной форме
- •2.7. Реакция пассивных элементов на гармоническое воздействие
- •2.8. Комплексные схемы замещения
- •2.9. Законы Кирхгофа в комплексной форме
- •2.10. Энергетические процессы в цепях с источниками гармонического сигнала
- •2.11. Качественное построение вд в простых схемах
- •3. Анализ простых схем замещения с источниками гармонического сигнала
- •3.1. Последовательное соединение элементов
- •3.2. Параллельное соединение элементов r, l, c
- •3.3. Измерительные приборы в схемах
- •3.4. Метод эквивалентных преобразований в простых схемах
- •3.5. Измерение мощности
- •3.6. Резонанс в электрических схемах с источниками гармонического сигнала
- •4. Методы расчета сложных схем
- •4.1. Расчет электрических схем по законам Кирхгофа
- •4.2. Особенности составления систем уравнений по законам Кирхгофа для схем с управляемыми источниками
- •4.3. Метод узловых потенциалов
- •4.4. Особенности составления системы по муп в схемах с управляемыми источниками
- •4.5. Метод контурных токов
- •4.6. Особенности составления системы уравнений мкт в схемах с управляемыми источниками
- •5. Переходные процессы в линейных электрических схемах
- •5.1. Основные понятия. Законы коммутации
- •5.2. Классический метод анализа переходных процессов
- •5.3. Начальные условия. Независимые начальные условия
- •5.4. Зависимые начальные условия
- •5.5. Составление характеристического уравнения и определение его корней
- •5.6. Принужденная составляющая
- •5.7. Определение постоянной интегрирования
- •5.8. Построение графика найденной функции I(t) или u(t)
- •5.9. Алгоритм решения задачи классическим методом
- •5.10. Особенности расчета переходных процессов в схемах второго
- •5.11. Переходная характеристика
- •5.12. Анализ переходных процессов в линейных схемах
- •6. Метод наложения
- •7. Теорема взаимности
- •8. Расчет линейных схем с источниками периодического негармонического сигнала
- •8.1. Представление функции в виде ряда Фурье
- •8.2. Расчет схем с источниками негармонического
- •8.3. Амплитудно-частотный и фазочастотный спектры
- •8.4. Расчет мощности в схемах с источниками
- •9. Расчет схем с индуктивными связями
- •9.1. Основные определения
- •9.2. Расчет комплексных схем со взаимно–индуктивными связями
- •10. Обзор методов анализа схем
5.8. Построение графика найденной функции I(t) или u(t)
Прежде, чем строить
график функции, необходимо записать ее
с подста-новкой найденных значений А1,
ρ1
и
или
![]() :
:
.
Пусть
= const = I, то есть в схеме после коммутации
включен источник постоянного сигнала.
Построение графика начинаем с построения
экспоненты
![]() ,
то есть свободной составляющей искомой
функции.
,
то есть свободной составляющей искомой
функции.
Для построения экспоненты необходимо определить постоянную затухания τ, которая показывает, как быстро затухает процесс:
τ = | ρ1 |−1 .
 Через
(3 – 5)τ переходные процессы практически
затухают, а экспонента сходит к нулю.
Таким образом, для построения свободной
составляющей качественно достаточно
двух значений: при t = 0 функция равна А1
и при t = 5τ функция равна нулю. Если А1
< 0, то ее значение откладывается на
отрицательной полуоси (рис. 5.44)
Через
(3 – 5)τ переходные процессы практически
затухают, а экспонента сходит к нулю.
Таким образом, для построения свободной
составляющей качественно достаточно
двух значений: при t = 0 функция равна А1
и при t = 5τ функция равна нулю. Если А1
< 0, то ее значение откладывается на
отрицательной полуоси (рис. 5.44)
.
рис. 5.44
Очевидно, чем больше модуль | ρ1 | корня характеристического уравнения, тем быстрее заканчивается переходной процесс, то есть тем меньше τ. Исследуя зависимость параметра ρ1 от параметров схемы R, L или С, можно ответить на вопрос, как изменить время переходного процесса 5τ.
После построения свободной составляющей в тех же осях строится принужденная составляющая. Поскольку она постоянна, её график – это прямая, параллельная оси времени t (рис. 5.45).
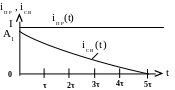
рис. 5.45
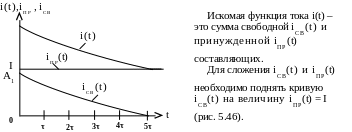
рис. 5.46
Если принужденная
составляющая – гармоническая функция
времени
![]() ,
то в качестве оси абсцисс вместо времени
t целесообразно взять фазу
,
то в качестве оси абсцисс вместо времени
t целесообразно взять фазу
![]() − относительное время.
− относительное время.
Для построения в
одних осях свободной и принужденной
составляющих необходимо определить
период
![]() принужденных колебаний. Воз-
принужденных колебаний. Воз-
можны три варианта
соотношения периода
![]() и постоянной затухания τ:
и постоянной затухания τ:
![]() .
.
Если
![]() то
за время переходного процесса уложится
лишь часть полного периода
то
за время переходного процесса уложится
лишь часть полного периода
![]() .
.
Если
![]() то
за время переходного процесса уложится,
как минимум, один целый период
.
то
за время переходного процесса уложится,
как минимум, один целый период
.
Если же
![]() то
за время переходного процесса уложится
ровно один целый период
.
то
за время переходного процесса уложится
ровно один целый период
.
Рассмотрим
последний случай. Пусть для определенности
![]() >
А1.
Строим экспоненту с уровнем
>
А1.
Строим экспоненту с уровнем
![]() при t = 0 и нулевым уровнем при
при t = 0 и нулевым уровнем при
![]() ,
это кривая свободной составляющей
,
это кривая свободной составляющей
![]() .
Строим синусоиду с амплитудой
.
Строим синусоиду с амплитудой
![]() и нулевой начальной фазой (пунктир) с
периодом
и нулевой начальной фазой (пунктир) с
периодом
![]() (пунктир). Сдвигаем её влево по оси
(пунктир). Сдвигаем её влево по оси
![]() на величину начальной фазы ψ. В результате
получаем кривую принужденной составляющей
на величину начальной фазы ψ. В результате
получаем кривую принужденной составляющей
![]() .
Для построения кривой суммы свободной
и принужденной составляющих
.
Для построения кривой суммы свободной
и принужденной составляющих
![]() сложим значения этих функций для
характерных моментов времени (рис.
5.47).
сложим значения этих функций для
характерных моментов времени (рис.
5.47).
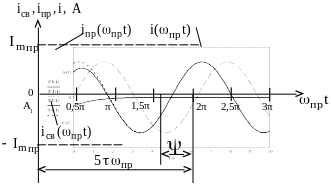
рис. 5.47
Обязательно нужно рассматривать те моменты времени, для которых принужденная составляющая имеет экстремумы и нули.
Для качественного построения кривой достаточно 5 – 6 точек.
Все изложенное справедливо и для функции напряжения u(t) при замене
на
,
![]() и i(t) на u(t) соответственно.
и i(t) на u(t) соответственно.
