5.6. Принужденная составляющая
Принужденная составляющая iПР(t) или uПР(t) исследуемого тока или напряжения определяется из расчета схемы после коммутации в установившемся режиме при t → ∞, когда переходные процессы завершились.
Алгоритм определения принужденной составляющей
1. Воссоздается схема после коммутации.
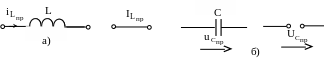2.
если
в схеме после коммутации включен источник
постоянного сигнала, то переходим к
эквивалентной схеме по постоянному
току (рис. 5.39,а; 5.39,б):
,
Рис. 5.39
В полученной схеме определяется значение принужденного тока или напряжения любым удобным методом:
или
.
3. Если в схеме
после коммутации включен источник
гармонического сигнала
,
то необходимо перейти к комплексной
схеме замещения:
.
Любым удобным методом определяется комплексное амплитудное значение искомого тока или напряжения .
4. Осуществляется переход от комплексного амплитудного значения тока или напряжения к гармонической функции принужденного тока или напряжения
или
.
5. Определяется значение принужденного тока или напряжения при t = 0:
или
.
Если в схеме после коммутации источник отсутствует, то принуж денное значение любого тока или напряжения равно нулю.
Пример 43. Определить в схеме (рис. 5.40):
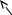
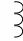
е(t)
R2
L
R1
рис. 5.40
Схема после коммутации имеет вид (рис. 5.41):
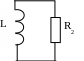
рис. 5.41
Источник в схеме после коммутации отсутствует, поэтому:
.
Пример 44. Дана схема (рис. 5.42).
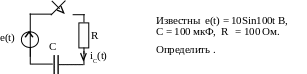
рис. 5.42
Воссоздаем схему после коммутации (рис. 5.43,а) и переходим к комплексной схеме замещения (рис. 5.43,б), поскольку в схеме присутствует источник гармонического сигнала:
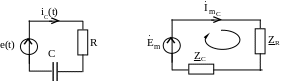
а) б)
Рис. 5.43
В.
100
Ом,
Ом.
На основании II закона Кирхгофа:
.
= 10·(100 − j100)−1
= 10·(141·
)−1
= 0,07
А.
0,07
А.
Переходим к гармонической функции принужденного тока:
А .
Определяем значение
при t = 0:
= 0,05 А.
5.7. Определение постоянной интегрирования
Функция тока или напряжения в схемах первого порядка классическим методом определится в виде:
или
.
Положим t = 0, тогда:
или
.
Из последних уравнений постоянная интегрирования А1 определится:
или
.
Таким образом, для определения постоянной интегрирования А1 необходимо найти начальное условие i(0) или u(0) и принужденное значение тока
или напряжения
.