5.4. Зависимые начальные условия
К зависимым
начальным условиям (ЗНУ) относятся все
напряжения и токи, кроме
и
,
в момент коммутации. Например, по условию
задачи необходимо определить ток
емкости. Искомым ЗНУ будет
.
Иногда ЗНУ не нужны для решения задачи, если по условию задачи необходимо найти ННУ.
Алгоритм определения ЗНУ
1. Начинаем со схемы после коммутации.
2. Составляем систему уравнений по II закону Кирхгофа во временной области.
3. Полагаем t = 0 и подставляем в систему уравнений из п. 2.
4. В полученную по п. 3 систему подставляем ранее найденные ННУ.
5. Решаем полученную
систему относительно искомого ЗНУ,
предварительно выразив напряжения на
активных сопротивлениях
через токи
.
Пример 36. Определить в следующей схеме (рис. 5.15):
Рис. 5.15
Схема после коммутации имеет вид (рис. 5.16):
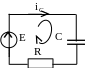
Рис. 5.16
По II закону Кирхгофа для такой схемы справедливо уравнение:
Полагаем t = 0,
,
ННУ для этой задачи
=
0, тогда
,
но
Итак,
Пример 37.
Определить
в следующей схеме (рис. 5.17).
Рис. 5.17
Схема после коммутации имеет вид (рис. 5.18):
Рис. 5.18
По I закону Кирхгофа можно составить одно уравнение:
.
По II закону Кирхгофа можно составить два уравнения, так как в схеме две главные ветви:
Полагая t = 0, получим:
где е(0) = 10sin(100t
+
)
= 5 В.
ННУ
,
так как до коммутации источник был
отключен. Выражения
и
подставляем в систему уравнений по II
закону Кирхгофа:
Таким образом систему из трех уравнений решаем относительно трех неизвестных.
Из первого уравнения
имеем
.
Вычитаем третье уравнение из второго:
Учитывая, что и R1 = R2, получим:
или
.
Итак, .
В более сложных схемах система уравнений по законам Кирхгофа может оказаться более высокого порядка. В этих случаях её решение занимает много времени. Есть другой путь её решения.
Рассмотрим схему в момент коммутации сразу после коммутации. Индуктивность в этой схеме заменена источником тока, величина которого равна току индуктивности в момент коммутации, то есть ННУ iL(0) (рис. 5.19).
=
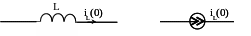
Рис. 5.19
Емкость в схеме после коммутации заменена источником напряжения (э.д.с.), величина которого равна напряжению на емкости в момент коммутации, то есть ННУ uС(0) (рис. 5.20).
Рис. 5.20
Очевидно, что при
нулевых ННУ, то есть при
или
,
источники исключаются из схемы:
означает,
что ток источника тока равен нулю,
источник заменяется обрывом (рис. 5.21);
означает, что напряжение источника
равно нулю, источник заменяется коротко
замкнутым соединением (рис. 5.22)
= =
Рис. 5.21
= =
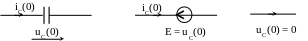
Рис. 5.22
Полученную схему можно решать любым методом: МКТ, МУП, по формулам разброса.
Пример 38.
Рассмотрим еще раз схему примера
37. Поскольку ННУ
,
то
в момент коммутации в месте включения
индуктивности будет
обрыв (рис.
5.23). Необходимо определить напряжение
на полюсах
обрыва:
Рис. 5.23
По II закону Кирхгофа для контура:
,
Поскольку
,
то
5·(100+100)−1
= 0,025 А ,
0,025·100 = 2,5 В.
Пример 39.
Определить
в следующей схеме (рис. 5.24):
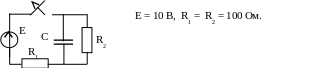
Рис. 5.24
ННУ
.
Схема после коммутации имеет вид (рис. 5.25):
i2
iС
С
R2
е1=
uС(0)
R2
uС
iС(0)
Рис. 5.25
= –5 · 100−1
= –0,05 А .
Итак, iС(0) = – 0,05 А .
Пример 40. Определить i1(0) после коммутации в следующей схеме (рис. 5.26):
Рис. 5.26
Начинаем со схемы до коммутации, чтобы определить ННУ (рис. 5.27,а).
Поскольку в схеме до коммутации включен источник постоянной э.д.с., переходим к эквивалентной схеме по постоянному току (рис. 5.27,б):
а) б)
Рис. 5.27
10·100−1
= 0,1 А .
Сопротивление R2 закорочено индуктивностью.
Для определения ЗНУ i1(0) переходим к схеме после коммутации (рис.5.28,а). Включаем источник тока I0 = iL(0) = 0,1 А (рис. 5.28,б).
а) б)
Рис. 5.28
Из схемы после коммутации для t = 0 видно, что ток i1(0) равен току источника I0 , следовательно:
i1(0) = iL(0) = 0,1 А .