4.6. Особенности составления системы уравнений мкт в схемах с управляемыми источниками

Если в схеме включены источники, управляемые токами ветвей (ИНУТ

или ИТУТ), то необходимо эти токи ветвей выразить через контурные токи и подставить в каноническую систему уравнений по МКТ.

Если в схеме включены источники, управляемые напряжением на участке схемы (ИНУН или ИТУН), то необходимо управляющее напряжение выразить через контурные токи и подставить в каноническую систему уравнений по МКТ.

Пример 32. Составить систему расчетных уравнений по МКТ для схемы (рис. 4.31) с заданными параметрами: .

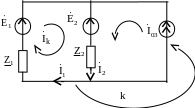
Рис. 4.31

С троим дерево и граф схемы (рис. 4.32), из которого следует, что главных ветвей одна, следовательно, имеется один независимый контур, один неизвестный контурный ток .

Рис. 4.32

Поскольку в схеме имеется источник тока , вводим дополнительный контурный ток. Уравнение по МКТ имеет вид:

.

Выражаем управляемый ток через контурный , но следовательно .

или

.

5. Переходные процессы в линейных электрических схемах

5.1. Основные понятия. Законы коммутации

В электрических схемах возможны два режима работы: установившийся и переходный.

Режим называется установившемся, если закон изменения тока или напряжения на исследуемом интервале времени не изменяется. Так, если в схеме включен источник постоянного тока или напряжения, на исследуемом интервале времени напряжение или ток будут постоянными: U = const или I = const

(рис. 5.1, а). Если в схеме включен источник гармонического сигнала, то любой ток или напряжение будут изменяться по гармоническому закону, но закон этот изменяться не будет (рис. 5.1,б).

а) б)

Рис. 5.1

Например, в схеме до коммутации источник был отключен, следовательно, ток в каком-то элементе был равен нулю. в момент t = 0 прошла коммутация – включили источник.

Рис. 5.2

В установившемся режиме после коммутации ток стал равен постоянной величине I. Между этими установившимися режимами переходной процесс

(рис. 5.2).

Если в схеме включить или отключить какие-то элементы, то, очевидно, до коммутации будет одна схема, а после коммутации – другая. В первой схеме будет один установившейся режим, а во второй – другой.

Переходный режим или процесс – это режим перехода от одного установившегося режима работы электрической схемы к другому под действием коммутации.

Коммутация – мгновенное изменение топологии и (или) параметров схемы.

В схемах коммутация обозначается ключом. Существует два вида ключей, работающих на замыкание (рис. 5.3,а) и размыкание (рис. 5.3,б):

на замыкание на размыкание

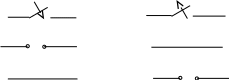
до коммутации до коммутации

после коммутации после коммутации

а) б)

Рис. 5.3

Если в схеме есть ключ на замыкание, то до коммутации в месте ключа до коммутации был разрыв, а после замыкания – коротко замкнутое соединение. Если же ключ на размыкание, то в схеме до коммутации было коротко замкнутое соединение, а после коммутации появился разрыв.

Рассмотрим, например, схему с ключом на замыкание (рис. 5.4,а).До коммутации в схеме был разрыв в месте ключа, то есть источник э.д.с. был отключен, ток не проходил. После коммутации в месте ключа появилось коротко замкнутое соединение (рис. 5.4,б).

а) б)

Рис. 5.4

С точки зрения физики переходные процессы – это переход от одного энергетического состояния (в схеме до коммутации) к другому энергетическому состоянию (в схеме после коммутации).

Так, в приведенной схеме (рис. 5.4,а) до коммутации емкость не заряжена, поэтому ее энергия равна нулю. В схеме после коммутации емкость заряжается. То есть в неё поступает энергия электрического поля.

Таким образом, необходимыми условиями переходного процесса являются, во-первых, коммутация, а во-вторых, наличие в схеме после коммутации реактивных элементов – емкости или индуктивности, энергия которых изменяется. Что касается активного сопротивления, то там тоже могут быть переходные процессы, но связаны они с изменением энергии теплового поля. Эти изменения проходят гораздо медленнее, чем изменения электрического или магнитного полей.

Переходные процессы подчиняются законам коммутации. Любой реальный источник энергии может отдавать только конечную мощность, поэтому суммарная энергия, запасенная в схеме, может изменяться только плавно, не скачком.

Рассмотрим схему (рис. 5.5):

Рис. 5.5

По II закону Кирхгофа после коммутации

.

Ток i(t) и э.д.с. Е могут принимать только конечные значения.

Допустим, что ток i(t) изменился скачком, то есть за бесконечно малый промежуток времени t → 0 ток изменился на конечную величину Δi . Тогда Δi(Δt)⁻¹ → ∞, Е → ∞, то есть не выполняется второй закон Кирхгофа.

Первый закон коммутации

Ток индуктивности не может изменяться скачком, то есть ток индуктивности в схеме до коммутации равен току индуктивности в схеме после коммутации и определяется в момент коммутации.

Математически закон записывается в виде:

.

Если момент коммутации принять за начало отсчета времени, то есть , то закон может быть записан в виде:

,

где − ток индуктивности в схеме до и после коммутации соответственно.

Второй закон коммутации

Напряжение на емкости не может изменяться скачком, то есть напряже-

ние на емкости в схеме до коммутации равно напряжению на емкости после коммутации и определяется в момент коммутации:

.

Если , то .

Задача анализа переходных процессов заключается в определении мгновенных значений токов и напряжений всех ветвей схемы за определенный промежуток времени.

Функционирование схемы по законам Кирхгофа описывается системой дифференциальных уравнений. Такую систему можно решить классическим или операторным методами.

,