4.4. Особенности составления системы по муп в схемах с управляемыми источниками

В систему уравнений по МУП должны входить только потенциалы, которые определяются, и заданные параметры элементов, в том числе токи независимых источников э.д.с.

Если в схеме ИНУН или ИТУН , то необходимо управляющее напряжение выразить через потенциалы узлов схемы

( рис. 4.18 и рис. 4.19).

Если − напряжение на полюсах ветви, то , где − потенциалы узлов, которые войдут в систему МУП.

Рис. 4.18

Е сли − напряжение на участке ветви, то уравнение по II закону Кирхгофа для ветви примет вид:

или

Рис. 4.19 ,

.

Потенциалы узлов входят в систему МУП.

Если в схеме ИНУТ , то необходимый ток j-ой ветви выразится через потенциалы узлов, прилегающих к j-ой ветви (рис. 4.20 и рис. 4.21):

Рис. 4.20

и ли

→ .

Рис. 4.21

Если в схеме ИТУТ , то необходимо управляющий ток выразить через потенциалы (аналогично предыдущему случаю).

Пример 28. Рассмотрим схему (рис. 4.22):

1

− независимые источники э.д.с.

4

− управляемый напряжением источник тока:

.

2

3

Требуется составить систему

уравнений по МУП.

k

Рис. 4.22

Примем = 0, тогда:

для узла 1:

,

для узла 3:

.

Учитывая, что , запишем или .

Подставляя полученный результат в уравнение для узла 3, получим:

или

.

В последнем уравнении остаются два неизвестных . Оно легко решается совместно с уравнением для узла 1.

Таким образом, к алгоритму МУП добавляется ещё один пункт. После составления канонической системы уравнений необходимо выразить параметры управляемых источников через их управляющие параметры, а затем выразить управляющие параметры через потенциалы узлов схемы.

4.5. Метод контурных токов

Суть метода контурных токов (ИКТ) заключается в том, что вводятся условные контурные токи, как правило, равные токам главных ветвей, для которых составляется система уравнений по II закону Кирхгофа. Следовательно, число Х_МКТ уравнений по МКТ равно числу главных ветвей схемы, числу независимых контуров и числу уравнений по II закону Кирхгофа: Х_МКТ = Х_II.

Каждое уравнение системы составляется для конкретного независимого контура. Система решается относительно контурных токов, а затем токи ветвей определяются через контурные токи.

Каноническая система уравнений по МКТ имеет вид:

где − соответственно 1-й, 2-й, 3-й …n-ый контурные токи, относительно которых решается система уравнений;

− собственное сопротивление соответственно 1-го, 2-го, 3-го …n-го контура;

, где j ≠ m – общее сопротивление между j-ым и m-ым контурами;

− контурные э.д.с. соответственно 1-го, 2-го, 3-го, … n-го контуров.

Собственное сопротивление контура определяется как сумма сопротивлений, входящих в данный контур ( рис. 4.23).

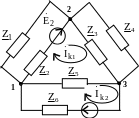
Рис. 4.23

Например, контур, контурный ток которого обозначен на схеме , включает сопротивления . Его собственное сопротивление определится .

Сомножители с собственными сопротивлениями входят в каноническую систему уравнений для МКТ со знаком плюс.

Общее сопротивление между j-ым и m-ым контурами определяется как сумма сопротивлений, входящих в j-ый и m-ый контуры.

Например, контур, контурный ток которого обозначен на схеме , содержит сопротивление , общее с контуром . Можно записать .

Сомножители с общим сопротивлением входят в каноническую систему уравнений для МКТ со знаком плюс, если направления контурных токов в нем совпадают, и со знаком минус – если не совпадают. В данном случае они не совпадают, поэтому сомножители должны входить в каноническую систему уравнений со знаком минус.

Контурная э.д.с. определяется как алгебраическая сумма э.д.с., входящих в данный контур:

,

где N_d – число э.д.с., входящих в d-ый контур.

Правило знаков. Э.д.с. берется со знаком плюс, если ее направление совпадает с направлением контурного тока, для которого составляется уравнение, и со знаком минус, если не совпадает. (рис. 4.24)

Рис. 4.24

Пример 29. Дана схема (рис. 4.25). Требуется составить систему уравнений по МКТ.

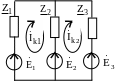
Рис. 4.25

Определяем число главных ветвей. Для этого строим граф схемы

(рис. 4.26):

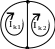
Рис. 4.26

Из графа видно, что в схеме две главных ветви. Обозначим направления контурных токов . Очевидно уравнений по МКТ будет два.

Для первого контура:

,

где − собственное сопротивление первого контура;

− общее сопротивление первого и второго контура;

− э.д.с. первого контура;

для второго контура:

,

где − собственное сопротивление второго контура;

− э.д.с. второго контура.

Система уравнений по МКТ имеет вид:

Если в схему включены источники тока, то нужно вводить дополнительные контурные токи, равные по величине токам источников тока и совпадающие с ними по направлению.

Дополнительный контур выбирается так, чтобы в него входил только один источник тока – тот, для которого вводится этот контур, и любые другие ветви схемы.

Дополнительные контурные токи не увеличивают количество уравнений МКТ, то есть порядка системы. Дополнительные контурные токи входят в левую часть канонической системы уравнений, если их контуры имеют общее сопротивление с независимыми контурами.

Пример 30. Рассмотрим схему, отличающуюся от предыдущей наличием ветви с источником тока (рис. 4.27).

Рис. 4.27

Очевидно, что граф схемы не изменится, так как ветвь с источником тока не входит в граф. Следовательно, как и в предыдущей схеме, будет два независимых контурных тока . Обозначим их в схеме.

Но поскольку включен источник тока , необходимо ввести дополнительный контурный ток , по величине равный и совпадающий с ним по направлению. Обозначим его в схеме = .

Теперь можно составить систему из двух уравнений по МКТ, исходя из канонической.

для первого контура:

.

Изменений в уравнении нет, так как нет общего сопротивления с контуром тока .

для второго контура:

,

Слагаемое вызвано дополнительным контурным током . Здесь − общее сопротивление между вторым и дополнительным контурами.

Записывая систему в канонической форме, необходимо слагаемое

перенести в правую часть, как величину известную, подставив = :

Алгоритм решения задачи МКТ

1. Задаемся направлениями токов ветвей.

2. Строим дерево и граф схемы, из которого определяем количество главных ветвей и независимых контуров.

3. Задаемся направлениями контурных токов независимых контуров(произвольно, по или против часовой стрелки).

4. Если в схеме есть источники тока, то вводим дополнительные контурные токи.

5. Составляем и решаем систему уравнений по МКТ, исходя из канонической.

6. Определяем токи ветвей как алгебраические суммы проходящих через данные ветви контурных токов, при этом контурный ток берется со знаком "+", если его направление совпадает с направлением тока ветви, и со знаком минус , если не совпадает.

П ример 31. Дана схема с четырьмя источниками э.д.с и двумя источниками тока (рис. 4.28). Требуется определить токи ветвей по МКТ.

Рис. 4.28

Строим дерево и граф схемы (рис. 4.29).

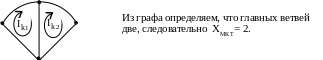
Рис. 4.29

Выбираем направления контурных токов . Поскольку в схеме имеется два источника тока и , необходимо ввести два дополнительных контурных тока, соответственно равных по величине токам источников и совпадающих с ними по направлению: и .

О бозначим направления всех контурных токов в схеме: независимых – сплошной линией, а дополнительных – пунктирной (рис. 4.30).

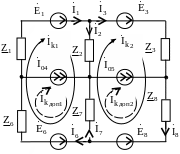Дополнительные контуры в принципе можно было выбрать

и иначе, например по ветвям:

для ,

для .

Нельзя выбирать дополнитель- ный контур лишь так, чтобы в него входили оба тока: и , и .

Рис. 4.30

Записываем уравнения по МКТ:

для первого контура:

;

для второго контура:

.

Переписываем систему в канонической форме:

Определяем токи ветвей, считая, что система решена относительно токов :

Несколько слов о матричной форме решения канонической системы уравнений по МКТ.

Как уже отмечалось, контурные токи можно определить по формулам:

где

, ,

, … , .
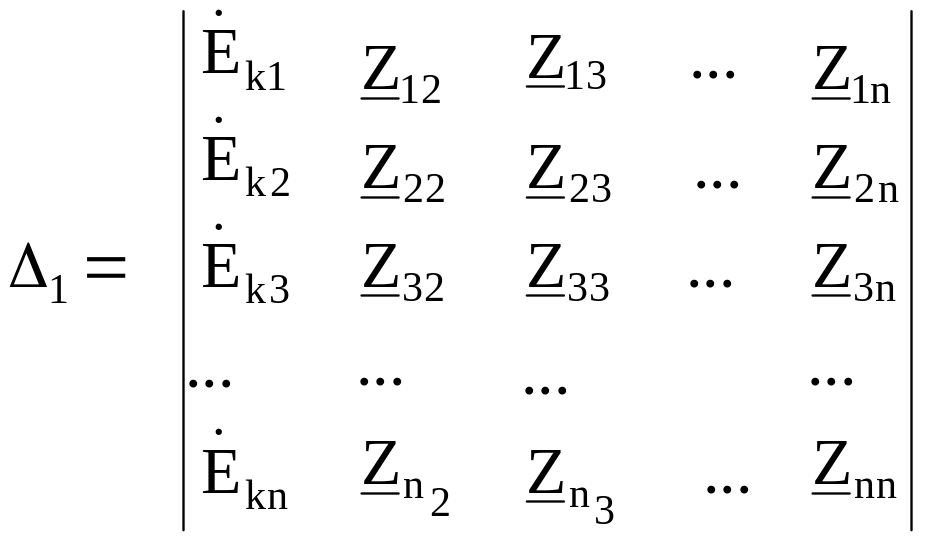