4.2. Особенности составления систем уравнений по законам Кирхгофа для схем с управляемыми источниками

Пусть задана схема (рис. 4.5) с управляемыми ИТУТ и ИНУН.

Рис. 4.5

Заданы полюсные уравнения:

где .

Следуя алгоритму составления системы уравнений, строим дерево и граф схемы (рис. 4.6):

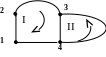
Рис. 4.6

Поскольку в графе две главные ветви, то имеем два независимых контура (I и II).

Задаемся направлениями токов в ветвях и направлениями обхода контуров и составляем уравнения по законам Кирхгофа.

Х_I = у – 1 = 4 – 1 = 3.

1. ;

2. ;

3. .

Х_II = 2.

для контура I: ;

для контура II: .

Подставим полюсные уравнения ИТУТ и ИНУН в систему уравнений по закону Кирхгофа:

Таким образом, в алгоритм решения задачи добавляется операция выражения всех управляемых источников через управляющие величины с помощью полюсных уравнений, при этом управляющие напряжения выражаются через токи, так как система уравнений решается через токи ветвей.

4.3. Метод узловых потенциалов

Суть метода узловых потенциалов (МУП) заключается в том, что из системы у − 1 уравнений определяются потенциалы узлов схемы по отношению к базисному узлу, а потом токи ветвей выражаются через потенциалы узлов, примыкающих к каждой из ветвей.

Таким образом, число уравнений по МУП равно числу Х_I уравнений по

I закону Кирхгофа Х_МУП = Х_I = у− 1. Прежде, чем составлять систему уравнений, потенциал одного из узлов (любого, но одного) принимается равным нулю. Такой узел называется базисным.

Каноническая система уравнений МУП имеет вид:

Здесь неизвестные потенциалы 1-го, 2-го, 3-го, …, n-го узлов;

− собственные проводимости 1-го, 2-го, 3-го, …, n-го узлов;

, где j ≠ k − общая проводимость между j−м и k−м узлами;

− узловые токи 1-го, 2-го, 3-го, …, n-го узлов.

Собственная проводимость узла определяется как сумма проводимостей всех ветвей, подходящих к данному узлу. Например, для n-го узла (рис. 4.7) собственная проводимость определится:

Рис. 4.7

,

где − проводимость первой ветви;

− проводимость ветви с источником тока (его внутреннее сопро- тивление равно ∞), в дальнейшем она в уравнениях не учиты- вается;

− проводимость ветви, в которую последовательно включены сопротивления ;

− проводимость ветви с последовательно включенными источ- ником (его внутреннее сопротивление равно нулю) и со- противлением .

Сомножители с собственными проводимостями входят в каноническую систему уравнений для МУП со знаком плюс.

Общая проводимость , определяется как сумма проводимостей ветвей, соединяющих j−ый и k−ый узлы (рис. 4.8). Например, общая проводимость между м и k−м узлами определится:

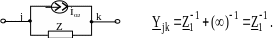
Рис. 4.8

Справедливо равенство

Сомножители с общими проводимостями входят в каноническую систему уравнений для МУП со знаком "минус".

Узловой ток узла равен алгебраической сумме токов от всех источников, включенных в ветвях, подключенных к данному узлу. Причем токи от источников тока учитываются алгебраической суммой , а токи от источников э.д.с. − алгебраической суммой , где N_i, N_e – соответственно число ветвей с источниками тока и источниками э.д.с., подходящих к данному узлу.

Правило знаков

Составляющая узлового тока берется со знаком плюс, если источник направлен к узлу, и со знаком минус , если от узла.

Например, для узла "n" (рис. 4.9) ток определится:

Рис. 4.9

В ветви с сопротивлением Z₃ нет тока, так как нет источника. Если ни в одной из ветвей, подходящих к узлу, нет тока, то узловой ток такого узла равен нулю.

Составим систему уравнений по МУП для схемы (рис. 4.10):

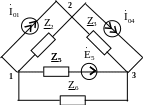
Рис. 4.10

Выберем базисный узел. Пусть . Х_МУП = 3 – 1 = 2.

Каждое уравнение системы составляется для конкретного узла схемы. Следовательно, система из двух уравнений составляется для узла "2" и узла "3".

Для узла 2:

.

Для узла 3:

.

Здесь − собственная проводимость узла 2;

− общая проводимость между узлами 2 и 3;

- узловой ток узла 2;

− собственная проводимость узла 3;

− общая проводимость между узлами 3 и 2;

- узловой ток узла 3.

Система уравнений по МУП принимает вид:

Потенциалы можно определить, например, по формулам:

,

где

− определитель системы,

, .

Токи ветвей можно определить через известные потенциалы узлов на основании закона Ома для участка цепи.

Для ветвей вида (рис. 4.11):

Рис. 4.11

Для ветвей вида (рис. 4.12 и рис. 4.13):

Рис. 4.12

Рис. 4.13

то есть если э.д.с. включается по направлению тока ветви, то она берется со знаком плюс, если против тока – со знаком минус.

В ветвях с идеальным источником э.д.с. ток определяется из уравнения по I закону Кирхгофа для любого из двух узлов, примыкающих к данной ветви. Например, для узла n (рис. 4.14):

Рис. 4.14

.

В канонической системе уравнений МУП такую ветвь описать нельзя, так как ее проводимость бесконечно большая. Поэтому есть два пути решения задачи.

Первый путь. Если ветвь с идеальным источником в схеме одна, то целесообразно выбрать один из узлов, примыкающих к данной ветви, в качестве базисного. Например, ветвь с источником (рис. 4.15):

Рис. 4.15

описывается уравнением (стрелка источника направлена к большему потенциалу). Если за базисный узел принять узел "n", то и для узла "k" . Если же за базисный узел принять узел "k", то уравнение для узла "n" имеет вид .

В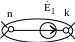 торой путь. Если в схеме больше одной ветви с идеальным источником э.д.с., то нужно вводить обобщенный узел или узлы. Обобщенный узел надо вводить так, чтобы замкнутый контур охватывал ветвь с идеальным источником э.д.с. (рис. 4.16):

Рис. 4.16

Для такого обобщенного узла, включающего два простых узла, будут справедливы два уравнения по МУП.

Уравнение внутренней связи – уравнение ветви с идеальным источником э.д.с.:

.

Уравнение внешней связи – это уравнение по структуре из канонической системы МУП, но так как два простых узла входят в обобщенный узел, то будет в два раза больше слагаемых слева и справа:

.

Алгоритм определения токов по МУП

1. Определить число уравнений Х_МУП = у− 1.

2. Выбрать базисный узел ( в общем случае произвольно).

3. Если в схеме включены ветви с идеальным источником э.д.с., то необходимо ввести обобщенные узлы.

4. Составить систему по МУП, исходя из канонической.

5. Решить систему относительно неизвестных потенциалов узлов.

6. Определить токи ветвей через известные потенциалы, задавшись их направлением.

Пример 27. Составить систему расчетных уравнений для следующей схемы (рис. 4.17):

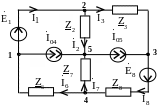
Рис. 4.17

Число Х_МУП уравнений по МУП:

Х_МУП = 5 – 1 = 4.

Выбираем базисный узел:

.

Вводим обобщенный узел 1−2 из узлов 1 и 2.

Уравнение внутренней связи:

.

Уравнение внешней связи:

,

для узла 3:

.

для узла 4:

.

Система уравнений в канонической форме:

Потенциалы определяются по формулам:

где Δ − определитель канонической системы,

Δ₁, Δ₂, Δ₃, Δ₄ – определители, полученные заменой в определителе Δ столб- ца, составленного из коэффициентов при соответственно столбцом из свободных членов.

Определим токи ветвей через потенциалы:

Для определения тока составляем уравнение по I закону Кирхгофа для узла 1:

.

Составим систему расчетных уравнений, принимая за базисный узел, примыкающий к ветви 1−2. Принимаем = 0, тогда:

для узла 2:

,

для узла 3:

,

для узла 4:

,

для узла 5:

.

Нельзя одновременно вводить обобщенный узел и брать за базисный один из узлов, примыкающих к ветви с идеальным источником э.д.с.

При расчете второй системы уравнений потенциалы узлов будут другие. Однако, токораспределение в схеме не зависит от абсолютных значений потенциалов узлов, а зависит лишь от разности потенциалов между узлами.