3.5. Измерение мощности

В ЭЦ мощность измеряется ваттметром. Ваттметр – прибор электродинамической системы, в котором есть две катушки: токовая и напряжения.

На электрических схемах ваттметр изображается следующим образом (рис. 3.43):

Рис. 3.43

У ваттметра на схемах две пары полюсов: токовые полюсы 1 – 2 и полюсы напряжения 3 – 4. Одноименные полюсы обозначаются звездочкой "*" и соединяются 3 – 1. Таким образом, через ваттметр идет ток от полюса со звездочкой *"1" к полюсу "2" и прикладывается напряжение к полюсам *"3" со звездочкой и "4". Ваттметр показывает активную мощность:

] .

Пример 24. Рассчитать баланс мощностей в приведенной схеме (рис. 3.44).

Рис. 3.44

Переходим к комплексной схеме замещения (рис. 3.45):

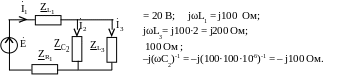
Рис. 3.45

Методом эквивалентных преобразований рассчитываем токи в ветвях схемы:

–j100·j200·(–j100+j200) = –j200 Ом;

Ом .

Схема приводится к виду (рис. 3.46):

Рис. 3.46

Из промежуточной схемы по формуле разброса определяем токи :

= 0,1414 ·j200·(–j100+j200)^–1 = 0,1414 ·2 = = 0,2828 А.

= 0,1414 ·(–j100)·(j100)^–1 = 0,1414 = = 0,1414 А.

В процессе расчета появился минус перед модулем. Это значит, что вектор необходимо развернуть на π, что и сделано.

Определяем полную комплексную мощность источника:

= 20·0,1414 = (2 – 2j) ВА.

Следовательно Р_ИСТ = 2 Вт, Q_ИСТ = –2 ВАР.

Определим активную мощность потребления

Р_ПОТР = ·R₁ = 0,1414² · 100 = 1,999 Вт.

Определим реактивную мощность потребления:

Q_ПОТР = = 0,1414²·100 + 0,1414²·200 – 0,2828²·100= = 0,01999·100 + 0,01999·200 – 0,07998·100 = 1,999 + 3,998 – 7,998 = –2,001 ВАР.

Определяем погрешность баланса:

Расчет показывает, что погрешность в пределах допустимой, следовательно, баланс мощностей выполняется.

3.6. Резонанс в электрических схемах с источниками гармонического сигнала

Параметры последовательного резонансного контура

Резонансом называется такой режим пассивной электрической схемы, содержащей индуктивности и емкости, при котором входное реактивное сопротивление или входная реактивная проводимость схемы равны нулю, следовательно, равна нулю реактивная мощность на входе схемы, а напряжение и ток на входе совпадают по фазе.

Рассмотрим пассивный двухполюсник, подключенный к источнику гармонического сигнала (рис. 3.47).

1

Рис. 3.47

Входное сопротивление двухполюсника – это эквивалентное сопротивление схемы, содержащейся в пассивном двухполюснике, относительно полюсов

1 – 2. Любое комплексное сопротивление можно представить в алгебраической форме:

= R_ВХ + jХ_ВХ,

где R_ВХ и jХ_ВХ – соответственно активное и реактивное сопротивление входа.

Комплексная входная проводимость может быть представлена в виде:

= g_ВХ + jb_ВХ ,

где g_ВХ и jb_ВХ – соответственно активная и реактивная составляющие входной проводимости.

По определению резонанс наступит в схеме, если Х_ВХ = 0 или b_ВХ = 0. Следовательно, сопротивление и проводимость при резонансе носят активный характер.

Различают два типа резонанса.

Резонанс напряжений наблюдается в схеме с последовательным соединением участков, содержащих индуктивности и емкости. При резонансе напряжений индуктивное сопротивление одной части схемы компенсируется емкостным сопротивлением другой части схемы:

X_L = X_C.

Резонанс токов наблюдается в схеме с параллельным соединением участков, содержащих индуктивности и емкости. При резонансе токов индуктивная проводимость одной части схемы компенсируется емкостной проводимостью другой части схемы, параллельно соединенной с первой:

b_L = b_C.

Рассмотрим подробно резонансный контур при последовательном соединении R, L, C элементов (рис. 3.48):

Рис. 3.48

Такой контур называется последовательным колебательным контуром, потому что идет перекачка магнитной и электрической энергий.

Комплексная схема замещения имеет вид (рис. 3.49):

Рис. 3.49

Существует пять параметров резонансного контура:

– частота резонанса ω₀ или f₀ ;

– волновое или характеристическое сопротивление ρ ;

– добротность контура Q;

– затухание контура d;

– полоса пропускания контура Δω₀ или Δf₀ .

Резонансная частота ω₀ определяется из основного соотношения:

X_L(ω₀) = X_C(ω₀) или X_L(ω₀) – X_C(ω₀) = 0.

Можно записать:

ω₀L = (ω₀С)^–1 или ω₀ = .

Таким образом, резонансная частота не зависит от активного сопротивления R контура.

Круговая ω₀ и линейная f₀ частоты связаны соотношением:

ω₀ = 2πf₀ .

В общем случае пассивного двухполюсника для определения резонансной частоты необходимо определить входное комплексное сопротивление , выделить его реактивную составляющую и приравнять её к нулю. Таким образом,

Х_ВХ(ω₀) = 0 – это уравнение для определения частот резонанса в любом пассивном двухполюснике.

Волновое (характеристическое) сопротивление ρ резонансного контура – это сопротивление индуктивности или емкости на резонансной частоте:

ρ = X_L(ω₀) = X_C(ω₀) = ω₀L = (ω₀С)^–1.

С учетом формулы для расчета ω₀ можно записать:

ρ = .

Добротность Q – это отношение волнового сопротивления к активному сопротивлению контура или, что то же самое, отношение напряжения на реактивном элементе к приложенному:

Q = ρ · R^–1 , но поскольку ρ = X_L(ω₀)

Q = R^–1 · .

При последовательном соединении ток один и тот же во всех элементах, следовательно U_L = I·X_L , U_C = I·Х_С, U_R = I·R = U_ВХ, так как Z_ВХ = R при

X_ВХ = 0.

Таким образом, Q = U_L(ω₀)· (ω₀) = I·X_L(ω₀)· (I·R)^-1 = U_С(ω₀)· (ω₀).

При увеличении активного сопротивления R контура его добротность Q уменьшается.

Добротность Q показывает, во сколько раз напряжение на реактивном элементе (индуктивности или емкости) превышает напряжение на входе контура.

Добротностью Q_К катушки индуктивности называется отношение:

Q_К = Х_K·R ,

где Х_K и R_К – сопротивления последовательно включенных индуктивного и активного элементов в схеме замещения катушки индуктивности.

Добротностью Q_С конденсатора называется отношение

Q_С = X_С·R ,

где X_С и R_с – сопротивления последовательно включенных емкостного и активного элементов в схеме замещения конденсатора.

Затухание d контура – величина, обратная добротности.

d = R·ρ^-1 = R · .

Полоса пропускания Δω₀ резонансного контура – это полоса частот вблизи резонансной частоты ω₀, на границах которой ток снижается до 0,707 резонансного тока I_max.

Рассмотрим зависимости I(ω), U_L(ω) и U_С(ω). Построим их в одних координатах (рис. 3.50). Для последовательного контура модуль тока I связан с модулями сопротивлений R, ωL и (ωС)^-1 соотношением:

.

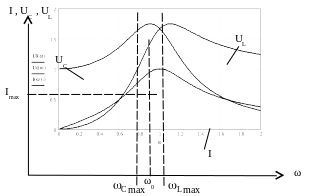
Рис. 3.50

Рассмотрим зависимость I(ω) при трех значениях частоты ω.

Пусть ω = 0. Это режим постоянного тока. С позиции физики индуктивность превращается в коротко замкнутое соединение, а емкость – в обрыв. Схема замещения контура примет вид (рис. 3.51):

Рис. 3.51

При ω → ∞ сопротивление индуктивности ωL→ ∞, а емкости (ωС)^-1 → 0, то есть индуктивность становится обрывом, а емкость – коротко замкнутым соединением (рис. 3.52). Схема замещения примет вид:

Рис. 3.52

Рассмотрим режим, когда ω = ω₀. В этом случае ωL = (ωС)^-1, то есть

Z == Z_min = R, следовательно на резонансной частоте ток имеет максимальное значение i(ω₀) = I_max.

Рассмотрим зависимости U_L(ω) и U_С(ω) при постоянных R , L, С.

Зависимость U_L(ω)

U_L = I·X_L = .

При ω = 0 Х_L = 0, следовательно U_L = 0.

При ω → ∞ U_L → Е, так как на индуктивности обрыв и напряжение Е прикладывается к полюсам индуктивности.

При 0 < ω < ω₀ растет ток I, растет Х_L, следовательно растет и U_L.

При ω₀ < ω < ∞ ток I уменьшается, растет Х_L, следовательно, в этом диапазоне частот наступает максимум U_L(ω) при ω_Lmax > ω₀. Можно показать, что ω_Lmax связана с ω₀ соотношением:

.

Зависимость U_С(ω)

U_С = I·X_С = .

При ω = 0 емкость представляет собой разрыв, и э.д.с. прикладывается к её полюсам, то есть U_С(0) = Е.

При ω → ∞ сопротивление емкости Х_С → 0, следовательно и U_С(∞) = 0.

При 0 < ω < ω₀ ток I растет, a Х_C уменьшается с ростом ω, следовательно, при ω_Сmax < ω₀ наступает максимум функции U_С(ω). Можно показать, что ω_Сmax связана с ω₀ соотношением:

Чем больше затухание d, то есть чем больше активное сопротивление R,

тем больше расхождение частот . Чем меньше R, тем ближе

частоты к частоте ω₀ и друг к другу.

Рассмотрим зависимость φ(ω)

Для последовательного контура из треугольника сопротивлений следует соотношение (рис. 3.53):

Рис. 3.53

φ = arctg (X·R^-1) = arctg {R^-1·[ωL – (ωC)^-1]}

Исследуем эту зависимость и построим её график (рис. 3.54).

Рис. 3.54

При ω → 0 arctg (−∞) → − 0,5π. Нельзя рассматривать режим ω = 0, так как при постоянном токе угол сдвига фаз φ не имеет смысла.

При ω → ∞ arctg (∞)→ 0,5π.

При ω = ω₀ arctg0 = 0.

Если R₂ > R₁ , то Q₂ < Q₁ и φ₂ < φ₁.

Построим зависимость Z(ω) при R = Var.

Построим зависимости X_L = ωL, X_C = (ωC)^-1, (X_L – X_C), Z(ω) в одних координатах (рис. 3.55).

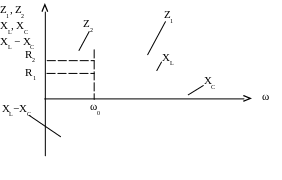
Рис. 3.55

На графиках (рис. 3.55) приведены зависимости X_L(ω), X_C(ω), их разность

X_L(ω) − X_C(ω) и две зависимости Z₁(ω) и Z₂(ω) для модуля комплексного сопротивления Z(ω), рассчитанные по формуле:

.

Зависимость Z₁(ω) соответствует R = R₁, а зависимость Z₂(ω) соответствует R = R₂, при этом R₂ > R₁ .

Нетрудно видеть, что модуль Z комплексного сопротивления имеет минимум, равный активному сопротивлению R контура на резонансной частоте ω₀. Модуль Z возрастает с отклонением частоты ω от резонансной и с уменьшением добротности Q контура.

В заключение несколько слов о влиянии резонансных явлений. Напряжения на индуктивности и емкости в режиме резонанса напряжений могут быть очень большими, а в сумме дают ноль. Это явление называется перенапряжением, оно отрицательно сказывается на изоляции, иногда ведет к пробою − повреждению изоляции.

Пример 25. Дана схема (рис. 3.56).

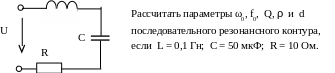
Рис. 3.56

Резонансная частота ω₀ определится:

ω₀ = = 10³∙( )^-1 = 447,2 рад/с;

f₀ = ω₀∙(2π)^-1 = 447,2∙(2∙3,14)^-1 = 71,2 Гц;

Q = X_L(ω₀)∙R^-1 = ω₀LR^-1 = 447,2∙0,1∙10^-1 = 4,472;

ρ = X_L(ω₀) = ω₀L = 447,2∙0,1 = 44,72 Ом ;

d = Q^-1 = (4,472)^-1 = 0,2236.