3.4. Метод эквивалентных преобразований в простых схемах

Два участка электрической схемы называются эквивалентными, если в результате замены одного другим токи и напряжения остальной части схемы не изменятся.

Преобразования схем называют эквивалентными, если некоторые участки этих схем заменяются эквивалентными.

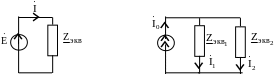Суть метода эквивалентных преобразований заключается в том, что исходная схема с помощью эквивалентных преобразований участков последовательного и параллельного соединений элементов сводится к одноконтурной, если в исходной схеме находится источник э.д.с (рис. 3.33,а), или к двухконтурной, если в исходной схеме источник тока (рис. 3.33,б):

а) б)

Рис. 3.33

В полученной одноконтурной схеме ток определяется на основании ΙΙ закона Кирхгофа. В схеме с источниками тока токи ветвей определяются на основании формулы разброса, которая гласит: ток в одной из двух параллельных ветвей равен току, подходящему к узлу, умноженному на сопротивление смежной ветви и деленному на сумму сопротивлений ветвей, включенных параллельно.

Таким образом, алгоритм решения задачи следующий.

1. Переходим к комплексной схеме замещения.

2. Сворачиваем схему к эквивалентной, начиная с ветвей, наиболее удаленных от источника.

3. Определяем ток ветви с источником.

4. Определяем токи остальных ветвей.

Рассмотрим схему с источником э.д.с. (рис. 3.34)

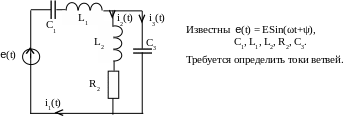
Рис. 3.34

В соответствии с алгоритмом переходим к комплексной схеме замещения (рис. 3.35):

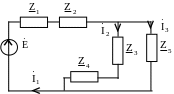
Рис. 3.35

Параметры комплексной схемы:

Начнем эквивалентные преобразования ветвей с , а также с и (рис. 3.36).

1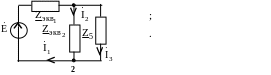

Рис. 3.36

1

В полученной схеме включены параллельно, поэтому схему можно преобразовать к виду (рис. 3.37):

Рис. 3.37

В полученной схеме включены последовательно, поэтому схему можно привести к окончательному виду (рис. 3.38):

Рис. 3.38

В полученной схеме ток определяется по ΙΙ закону Кирхгофа:

По формуле разброса из схемы с

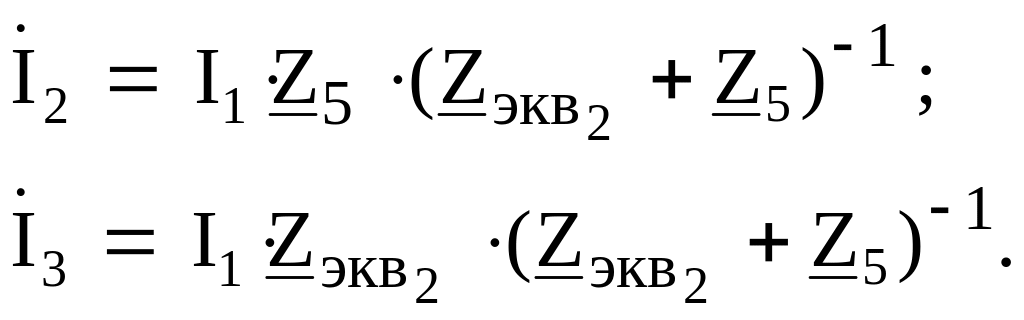
Формула разброса справедлива при указанных направлениях токов.

Пример 23. Дана схема (рис. 3.39).

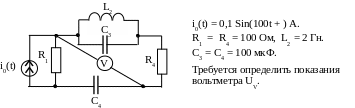
Рис. 3.39

Переходим к комплексной схеме замещения (рис. 3.40):

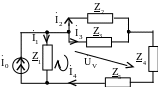
Рис. 3.40

= R₁ = 100 Ом ; Ом ;

Ом ;

= R₄ = 100 Ом ; Ом .

Комплексное действующее значение тока источника определится:

А.

Для определения напряжения, к которому подключен вольтметр, выберем контур, в который входит это напряжение, и составим для него уравнение по

ΙΙ закону Кирхгофа:

Для определения показания вольтметра предварительно нужно найти токи .

Для этого от исходной схемы переходим к эквивалентной (рис. 3.41):

Рис. 3.41

j200·(–j100)·(j200 – j100)^-1 = –j200 Ом.

Следующим этапом эквивалентных преобразований сворачиваем последовательное соединение (рис. 3.42):

Рис. 3.42

= –j200 + 100 –j100 = 100 – j300 = 316·е^–j0,4π.

В полученной схеме можно определить по формуле разброса:

А

А

А .

Определяем показания вольтметра: