3.2. Параллельное соединение элементов r, l, c
Соединение элементов называется параллельным, если к ним приложено одно и то же напряжение (рис. 3.15).
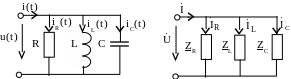
Рис. 3.15
По определению
.
По Ι закону Кирхгофа
.
,
где
.
Здесь
– эквивалентная проводимость
параллельного соединения.
Для приведенной
схемы
,
а в общем случае при параллельном
включении n элементов можно записать:
.
Если элементов
только два, то
следовательно
.
Таким образом,
.
Эквивалентная проводимость для приведенного соединения может быть представлена в виде:
,
–
модуль эквивалентной
проводимости парал-
лельного соединения.
Модуль Y может быть представлен в виде:
,
где bC = ωC и bL = (ωL)−1 – модули комплексной проводимости емкости и индуктивности соответственно.
В зависимости от соотношения модулей bC и bL возможны три режима работы параллельного контура:
bC > bL – характер соединения емкостной;
bC < bL – характер соединения индуктивный;
bC = bL – режим резонанса тока.
Рассмотрим первый режим (bC > bL)
Строим совмещенную ВД напряжения и токов (рис. 3.16):
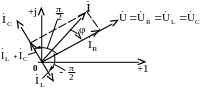
Рис. 3.16
Отложим вектор
напряжения
и
совпадающий с ним по направлению вектор
тока
.
Поскольку bC
> bL,
вектор тока
опережает вектор
на угол
,
а вектор тока
отстает от него на угол
,
причем длина вектора тока
меньше длины вектора тока
.
Сложив вектора
,
получим вектор
,
который по модулю равен разности
модулей этих векторов. Сложив вектор
с вектором
, получим вектор тока на входе параллельного соединения.
Из ВД следует, что угол сдвига фаз φ < 0.
Треугольники токов (рис. 3.17) и проводимости (рис. 3.18) имеют вид:
Рис. 3.17
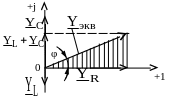
Рис. 3.18
Модули токов Ι, ΙR, ΙL и ΙC связаны соотношениями:
;
.
Рассмотрим теперь второй режим (bC < bL).
Строим совмещенную ВД токов и напряжения на входе (рис. 3.19):
Рис. 3.19
Из ВД видно, что
угол между векторами напряжения
и тока
> 0.
Модули токов Ι, ΙR, ΙL и ΙC связаны между собой соотношением:
.
В режиме резонанса
тока (bC
= bL)
выполняются условия ΙL
= ΙC,
=
ΙR.
Эквивалентная проводимость
при этом носит чисто активный характер
.
Совмещенная ВД токов и напряжения на входе принимает вид (рис. 3.20):
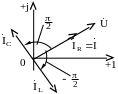
Рис. 3.20
Треугольники токов и проводимостей вырождаются: φ = 0.
Рассмотрим частотную зависимость параллельного контура. Графики зависимостей bL(ω) = (ωL)−1 и bC(ω) = ωC, построенные в одних координатах, имеют вид (рис. 3.21):
b
bС
bL
bL
= bС
ω
ω0
0
Рис. 3.21
В диапазоне частот 0 ≤ ω < ω0 bL > bC, характер соединения индуктивный.
В диапазоне ω0 < ω < ∞ bС > bL, характер соединения емкостной. При ω = ω0 bL = bC имеет место резонанс токов.