3. Анализ простых схем замещения с источниками гармонического сигнала

Схема называется простой, если она включает только один источник энергии, соединение элементов последовательное и (или) параллельное.

3.1. Последовательное соединение элементов

Соединение элементов называется последовательным, если через элементы идет один и тот же ток. Рассмотрим последовательное соединение элементов

R, L и C (рис. 3.1):

Рис. 3.1

Перейдем к комплексной схеме замещения (рис. 3.2):

Рис. 3.2

Поскольку элементы соединены последовательно, через них идет один и тот же ток, то есть .

Из ΙΙ закона Кирхгофа следует:

– = 0,

[−j(ωC)^-1] =

или

,

где – эквивалентное сопротивление последовательно соединенных элемен- тов.

j(ωC)^-1 = R + j[ωL – (ωC)^-1].

В общем случае для последовательного соединения элементов

.

Здесь n – число последовательно включенных элементов.

Для приведенной схемы R + j(X_L – X_C).

Очевидно, возможны три режима работы:

Х_L > X_C – схема носит индуктивный характер;

Х_L < X_C – схема носит емкостной характер;

Х_L = X_C – в последовательном контуре резонанс напряжений .

Рассмотри все три режима подробней.

Обозначим разнопотенциальные точки на комплексной схеме замещения (рис. 3.3):

Рис. 3.3

При индуктивном характере последовательного соединения Х_L > X_C, но

Ι_L = Ι_C, а U_L= Ι_L·X_L, U_C =Ι_C·X_C, следовательно, U_L > U_C.

Топографическая ВД напряжений для последовательного контура

Отложим вектор тока (с произвольной фазой, если нет расчета) на комплексной плоскости (рис. 3.4):

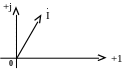
Рис. 3.4

Положим потенциал точки "0" равным нулю, φ₀ = 0, то есть поместим её в начало координат. Отложим вектор напряжения на емкости . Он отстает от вектора тока на угол . Длину вектора берем в отсутствие расчета произвольной (рис. 3.5).

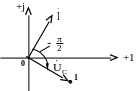
Рис. 3.5

Получим точку "1" на комплексной плоскости. Из точки "1" отложим вектор под углом к вектору тока , причем длина вектора , то есть

модуль U_L > U_C (по условию). Проведем его рядом, чтобы вектора

не сливались на ВД. Получим точку "2" на комплексной плоскости (рис. 3.6).

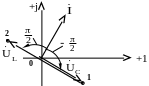
Рис. 3.6

Из точки "2" проведем вектор произвольной длины параллельно вектору тока , проходящему через сопротивление R. Получим точку "3" на комплексной плоскости. Соединим точки "О" и "3", получим вектор напряжения

на входе последовательного соединения (рис. 3.7):

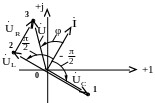
Рис. 3.7

Причем стрелка направлена к точке "3", так как φ₃ > φ₀, потому что ток течет от большего потенциала к меньшему. При построении ВД лучше идти всегда против тока, обходя контур, чтобы потенциал каждой последующей точки был выше предыдущей, тогда получим цепочку векторов.

Из ВД определим угол φ сдвига фаз, то есть угол, на который вектор напряжения опережает вектор тока или отстает от него.

– при индуктивном характере сопротивления. При φ = 0 – чисто активное сопротивление, а при – чисто индуктивное.

Из ВД можно построить треугольник напряжений (рис. 3.8).

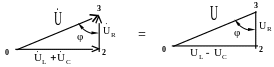
Рис. 3.8

Очевидно, для модулей напряжений (U_L – U_C)² + = U², следовательно , но U_R = Ι ·R, U_L = Ι ·X_L, U_C = Ι ·X_C, поэтому

, следовательно

,

φ = arctg [(U_L – U_C) · ] = arctg [(X_L – X_C) · R^–1].

Кроме треугольника напряжений можно построить треугольник сопротивлений (рис. 3.9).

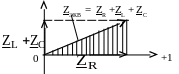
Рис. 3.9

Модули комплексных сопротивлений связаны соотношением:

.

Аналогичная ВД для емкостного режима, когда X_C > X_L и U_L < U_C, имеет вид (рис. 3.10):

Рис. 3.10

Треугольники напряжений (рис. 3.11) и сопротивлений (рис. 3.12), соответствующие этому режиму, имеют вид:

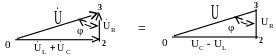
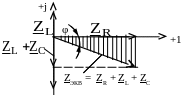Рис. 3.11

Рис. 3.12

Третий режим – режим резонанса напряжений, когда Х_С = X_L, u_L = u_C ,

, φ = 0. Напряжение на входе совпадает по фазе с током, проходящим в контуре (рис. 3.13):

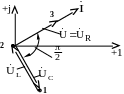
Рис. 3.13

Треугольники напряжений и сопротивлений вырождаются. Подробней об этом режиме будет сказано ниже.

Частотные зависимости последовательного контура

Ранее мы рассмотрели зависимости X_L(ω) и Х_С(ω). Совместим их в одних координатах рис. 3.14).

Рис. 3.14

Нетрудно видеть, что в диапазоне частот 0 ≤ ω < ω₀ Х_С > X_L, следовательно характер соединения емкостной. При ω = ω₀ Х_С = X_L имеет место резонанс напряжений. При ω₀ < ω < ∞ Х_L > X_С, следовательно характер соединения индуктивный.