5. Отклонение падающих тел к востоку от вертикали

Пусть точка М массы m падает без начальной скорости на Землю с высоты Н. Сопротивлением воздуха будем пренебрегать, а величину Н считаем малой по сравнению с радиусом Земли и поэтому не учитываем зависимость силы веса от расстояния. Возьмем систему координат, жестко связанную с Землей. Начало координат «О» совместим с точкой поверхности Земли, лежащей на одной вертикали с начальным положением падающего тела. Ось Z направим по истинной вертикали вверх, проведя ее через положение, занимаемое точкой в начальный момент времени. Ось X проведем по касательной к меридиану с севера на юг, ось У – по касательной к параллели с запада на восток (рис. 6). Полученную систему координат с достаточной степенью можно считать прямоугольной.

Для составления уравнения относительного движения к силе (притяжение Земли), нужно добавить силу инерции переносную и силу инерции Кориолиса , причем

Учитывая, что , уравнение относительного движения запишем в виде или проекциях на оси х, у, z.

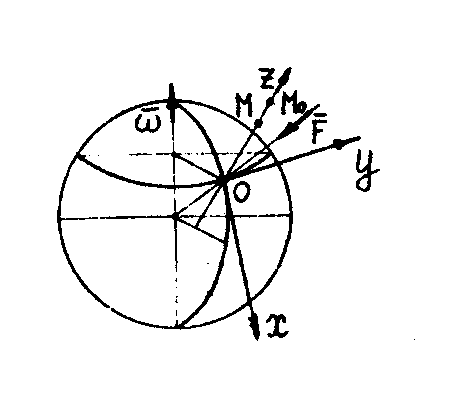
Рис. 6

(15)

Начальные условия при (16)

Так как сила Кориолиса очень мала по сравнению с силой тяжести, то в первом приближении можно считать вектор скорости направленным по вертикали, т.е. вдоль линии .

Тогда и уравнения (15) примут вид

. (17)

Используя начальные условия (16), решение системы дифференциальных уравнений (17) представим в виде

Найдем максимальное отклонение точки к востоку. При z=0 находим - время, за которое тело упадет на землю:

.

Подставляя в формулу для у, получим

.

Пусть тогда = 12,55 мм.

Неоднократно проводившиеся опыты подтверждают наличие восточного отклонения, близкого к теоретическому значению.

7. Вес и невесомость

Все, как было сказано выше, характеризуется силой давления тела на неподвижную относительно Земли горизонтальную опору, на которой тело расположено.

Под невесомостью материальной точки в какой-либо системе координат понимают отсутствие давления этой точки на тела, покоящиеся в этой системе координат. В качестве примера рассмотрим движение груза в лифте. Подвижную систему координат свяжем с лифтом, движущимся ускоренно относительно Земли, принятой за инерциальную систему отсчета. Груз будем считать материальной точкой, подвешенной на тросе к потолку (рис. 7).

7.1. Пусть лифт движется вверх с ускорением . На трос действуют две силы: сила тяжести натяжение троса . Чтобы составить уравнение относительного равновесия груза, нужно к силам, действующим на него, приложить переносную силу инерции . 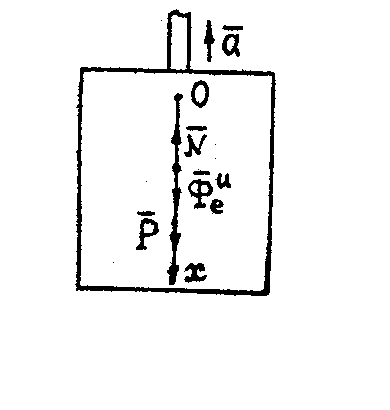Рис. 7

Уравнение относительного равновесия в проекции на подвижную ось x, скрепленную с лифом, примет вид O = P + ma - N. (18) Из уравнения (18) находим

N=P+ma=m (g+a). (19)

Наблюдаемое явление – кажущееся увеличение веса, ибо динамометр, вставленный между тросом и грузом, покажет силу m(g+a). Этот пример иллюстрирует те «перегрузки», которые возникают при ускоренном движении лифта, космического корабля и т.п.

7.2. Пусть теперь ускорение лифта направлено вниз . В этом случае наблюдаемые явления таковы: все незакрепленные предметы сближаются с потолком кабины ускоренным движением; если же предмет прикреплен при помощи троса с динамометром, то динамометр покажет силу N=m(g-a), т.к. сила инерции теперь направлена вверх. Так как сила инерции больше веса, предмет падает не на пол, а на потолок. Наблюдатель, находящийся в лифте, не может объяснить физический источник силы. С его точки зрения получается, что Земля не притягивает, а отталкивает груз.

Наблюдатель на Земле видит, что груз падает свободным падением с ускорением силы тяжести g, а лифт движется вниз с ускорением, большим, чем g, - поэтому лифт в своем движении перегоняет груз и потолок лифта ускоренным движением приближается к грузу.

7.3. Пусть теперь a=g, а лифт движется вниз. Наблюдаемые явления таковы: все предметы, даже незакрепленные, висят в воздухе, реакции всех тросов, на которых висят грузы, равны нулю, маятник, выведенный из вертикального положения, остается отклоненным и не колеблется (покажите последнее!)

Наблюдатель в кабине прикладывает к любому телу силу инерции, равную и противоположную силе веса; с его точки зрения в кабине как бы перестали действовать силы тяжести и все предметы находятся в состоянии невесомости (N=0).

Наблюдатель на земле видит, что лифт и все находящиеся в нем предметы падают с одним и тем же ускорением, т.е. движутся одинаково – поэтому перемещение предмета относительно кабины лифта равно нулю и он неподвижен относительно него. Такая же картина наблюдается в кабине космического корабля, движущегося в гравитационном поле Земли; как корабль, так и космонавт перемещаются с одним и тем же ускорением под действием одной и той ж силы притяжения к Земле – поэтому космонавт не передвигается относительно кабины, вися в ней. Наилучшей иллюстрацией этого является выход космонавта в космическое пространство.

8. План решения задач

1. Разложить «абсолютное» движение точки на относительное и переносное; выбрать неподвижную систему отсчета и подвижную, связанную с подвижной средой

2. Записать начальные условия относительного движения материальной точки

3. Изобразить силы, приложенные к материальной точке

4. Определить ускорение материальной точки в переносном движении , ускорение Кориолиса - , найти силу инерции в переносном движении , кориолисову силу инерции Добавить эти силы к силам, действующим на точку.

5. Составить дифференциальные уравнения относительного движения в проекциях на подвижные оси.

6. Проинтегрировать уравнения относительного движения, определить искомые величины, исследовать решение.

Замечание. Материальную точку следует изображать в промежуточном положении, соответствующем положительным координатам этой точки, и предположить, что точка движется в сторону возрастания этих координат. При относительном криволинейном движении удобно пользоваться дифференциальными уравнениями движения в проекциях на оси натурального триодра.

9. Пример. Ползун G (рис. 8) может скользить по хорде АВ равномерно вращающегося диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами с жесткостью с/2 каждая. Принимая ползун за точку массы m и пренебрегая трением, определить зависимость периода T его колебаний в относительном движении по хорде от угловой скорости диска.

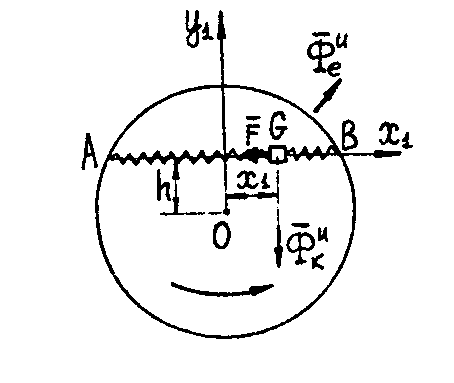
Рис. 8

Начало подвижной системы координат поместим в точке (положение статического груза). На груз действуют силы: сила тяжести, нормальная реакция хорды , упругая сила пружин . Первые две силы перпендикулярны плоскости чертежа и на рис. 8 не показаны. Сила упругости пропорциональна деформации пружин

.

Чтобы составить уравнения относительного движения, нужно к силам, действующим на точку, добавить переносную и кориолисову силы инерции:

.

Направления этих сил показаны на рис. 8.

.

В фигурных скобках указаны проекции переносной и кориолисовой силы инерции на подвижной оси и .

Дифференциальное уравнение относительного движения в векторной форме имеет вид

.

Или проектируя его на ось , получим

.

После элементарных преобразований это уравнение приводится к виду

.

Последнее уравнение выражает гармоническое колебание с периодом и не зависит от положения хорды.