Аналитическое представление логических функций. Дизъюнктивная и конъюнктивная нормальные формы
Аналитическое представление предполагает запись произвольной логической функции (ЛФ) в виде формул, переменными в которых являются известные ЛФ.
Дизъюнктивная нормальная форма(ДНФ) – это ЛФ, представляющая собой дизъюнкцию отдельных термов, каждый из которых есть некоторая ЛФ,
содержащая только конъюнкции и инверсии.
Например:
F(A,B,C)
=
Конъюнктивная нормальная форма (КНФ) - это ЛФ, предоставляющая собой конъюнкцию отдельных термов, каждый из которых есть ЛФ, содержащая только дизъюнктивную и инверсии.
Например:F(A,B,C)=
(
)(
).
Для однозначного представления ЛФ используются совершенные дизъюнктивная и конъюнктивная нормальные формы (СДНФ и СКНФ).
СДНФ - это дизъюнктивная форма, в которую входят конъюнкции только максимальные для данной ЛФ ранга.
Например, для функции трех переменных F(A,B,C) совершенной ДНФ будет представление:
F(A,B,C)=
v
v
v
v
.
Где каждая элементарная конъюнкция содержит три буквы.
Аналогично определяется СКНФ.
При получении нормальных форм ЛФ, а также при переходе от нормальных форм к совершенным формам обычно пользуются:
известными свойствами элементарных функций И, ИЛИ, НЕ
x
v
x
= x; x
v
1 = 1; x
v
0 = x; 
;
x
x
= x;
x
1 = x;
x
0 = 0;
.
законами:
ассоциативным (сочетательным):
x1 (x2x3) = (x1x2)x3 ,
x1 v (x2 v x3) = (x1 v x2) v x3 ;
коммутативным (переместительным):
x1x2 = x2x1
x1 v x2 = x2 v x1 ;
дистрибутивным (распределительным):
x1(x2 v x3) = (x1x2) v(x1x3) ,
x1 v (x2x3) = (x1 v x2) v(x1 v x3);
де Моргана:
,
склеивания и поглощения:
v
x1x2
= x1
,
(
)
v
x2
= x1
v
x2
.
Пример:
Упростить функцию в ДНФ:
F(x1,x2,x3)
=
.
Прежде всего, необходимо перевести эту функцию в СДНФ, т.к. только СДНФ дает единственное представление ЛФ, для чего воспользуемся свойствами дизъюнкции и конъюнкции.
x v x = 1; x 1 = x; x v 1 = 1.
Две
последних конъюнкции домножаем на (
)
и (
)
и приводим подобные члены:
F(x1,x2,x3)
=
=
=
=
=
=
=
.
Задачи:
1. Упростить ЛФ четырех переменных:
F(x1,x2,x3,x4)
=
.
2. Доказать, что F1(x1,x2,x3) = F2(x1,x2,x3), если
F1(x1,x2,x3)
=
;
F2(x1,x2,x3) = x1 v x2.
3. Преобразовать в СДНФ и СКНФ следующие функции, представление в ДНФ и КНФ:
а)
F1(x1,x2,x3)
=
;
б)
F1(x1,x2,x3)
=
.
4. Представление ЛФ в ДНФ и КНФ:
а)
F1(x1,x2,x3)
=
;
б)
F1(x1,x2,x3
) =
.
5. Упростить ЛФ, используя свойства элементарных функций:
а)
F1(x1,x2,x3)
=
;
б) F1(x1,x2,x3) = v1(1,2,3,4,5,6,7).
Практическая работа №2 Методы минимизации логических функций Логические функции небольшого числа переменных (n 3) можно минимизировать, используя тождества алгебры логики и законы алгебры логики.
При увеличении числа переменных (n < 6) можно использовать метод карт Карно.
Метод карт Карно
Алгоритм метода заключается в следующем:
а) объединяются клетки, составляющие полные квадраты из 4-х или 16-ти клеток;
б) объединяются клетки, составляющие полные столбцы или ряды из 2-х, 4-х или 8-ми клеток, а также 2 рядом расположенных столбца или ряда из 4-х, 16-ти или 8-ми клеток;
в) объединяются 2 соседние клетки в столбце или ряду.
В каждое объединение должно входить максимальное число клеток, одна клетка может входить в несколько объединений.
Если объединить клетки, незанятые , можно получить минимальную ДНФ (МДНФ) для инверсии функции F. Применив к F еще инверсию и закон де Моргана, можно получить минимальную КНФ (МКНФ).
Пример:
Минимизировать функцию
Карта Карно имеет вид:
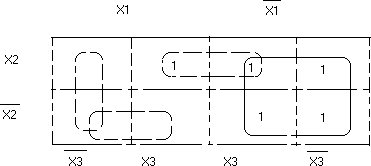
Получаем
F1(x1,x2,x3)
=
.
Объединяя клетки, не занятые 1, получаем МДНФ для инверсии функции
.
Инвертируя это выражение и применяя закон де Моргана, получаем МКНФ:
.
При большом числе переменных для минимизации ЛФ можно использовать метод Квайна-Мак-Класки или метод декомпозиции.
Метод декомпозиции
Он заключается в выделении более простых составляющих ЛФ и минимизации их по картам Карно, при этом
,
где функции F1 и F2 получаются из F путем подстановки в нее
значений x1=0 для x1=1 для F2.
Например,
F
=
=
3) Минимизация ЛФ в базисе И-НЕ
Алгоритм метода состоит в следующем:
а) получить МДНФ;
б) произвести двойную инверсию над полученной МДНФ;
в)
преобразовать по теореме де Моргана
инверсию дизъюнкции в конъюнкцию
инверсий по формуле
.
В результате получается ЛФ, содержащая только операции И-НЕ.
Например, пусть имеется МДНФ:
.
Производится двойная инверсия
=
и применяется закон де Моргана
=
.
4) Минимизация ЛФ в базисе ИЛИ-НЕ
Алгоритм метода состоит в следующем:
а) получить МДНФ;
б) произвести двойную инверсию конъюнкций в дизъюнкцию
инверсий;
в) преобразовать инверсию конъюнкций в дизъюнкцию инверсий:
.
В полученной ЛФ содержатся только операции ИЛИ-НЕ.
Например:
.
5) Минимизация ЛФ в базисе И - ИЛИ – НЕ
Алгоритм:
а) получить МДНФ для инверсии заданной ЛФ по картам Карно;
б) произвести инверсию полученной МДНФ:
Например,
;
.
Среди алгоритмов минимизации ЛФ от большого числа переменных, легко реализующихся на ЭВМ, наиболее распространен метод Квайна-Мак-Класки.
Задачи:
1. Минимизировать следующие ЛФ четырех с помощью карт Карно:
а)F = v1(0,2,5,7,8,10,15);
б)F = v1(1,3,4,5,6,7,10,11);
в)F = v1(0,2,7,8,13,15);
г)F = v1(0,2,3,4,5,7,13,15);
д)F = v1(0,3,5,7,8,11,12,15);
е)F = v1(5,6,7,9,10,11,14);
ж)F = v1(0,5,8,11,13,14,15);
з)F = v1(0,1,2,8,9,10,12,13,14,15).
2. Найти МДНФ методом Квайна-Мак-Класки:
а) F = v1(0,1,2,3,4,5,6,10,12,13,14);
б) F = v1(0,1,2,6,7,9,11,14,15).
3. Минимизировать с помощью карт Карно ЛФ:
F
=
(1,2,3,4,6,7,10,11,12,14).
4. Представить МДНФ, найденные в задаче 1, в базисах И-НЕ, ИЛИ-НЕ.
Литература
1) В.А. Горбатов. "Основы дискретной математики". М.: Высшая школа, 1986.
2) О.П. Кузнецов, Г.М. Адельсон-Вельский. "Дискретная математика для инженера", М.: Энерготомиздат, 1988.
3)
Лекции по теории графов / Емелигев В.А.
и др. - М.: Наука, 1990
Техника безопасности
при выполнении лабораторных работ
Общие требования безопасности
Опасные производственные факторы: воздействие на человека электрического тока, электрического поля, рентгеновского излучения, ультрафиолетового излучения.
Действия факторов: вследствие неисправности кабеля, электрической вилки (розетки), замыкания в цепи пользователь компьютера попадает под напряжение.
1.1. Студенты допускаются к работе в лаборатории после прохождения ими вводного инструктажа с оформлением соответствующей записи в журнале по технике безопасности, первичного инструктажа на рабочем месте с записью в журнале по охране труда. Инструктаж проводит заведующий кабинетом, лабораторией.
1.2. Запрещается оставлять рабочие места и ходить по лаборатории во время занятия.
1.3. Запрещается перестановка мониторов, клавиатуры, системных блоков, «мышей» и ковриков для «мышей» с одного рабочего места на другое.
1.4. Запрещается самостоятельное устранение неисправностей оборудования.
1.5. Запрещается нахождение в лаборатории в верхней одежде.