Підставимо останню формулу в диференціальне рівняння (12). Дістанемо

Розкриваємо косинус і синус суми аргументів і прирівнюємо множники при cos(t) і sin(t), оскільки ці функції є лінійно не­залежними:

З другого рівняння знаходимо рівняння для кута :

(13)

З першого рівняння знаходимо вираз для амплітуди струму

З рівняння (13) можна знайти cos і sin . Підставляючи їх у формулу для амплітуди струму I₀, дістанемо

(14)

Нагадаємо, що для схеми на рис. 5 R= R_мА. Повний опір кола, складеного з резистора з опором R_мА і конденсатора з ємністю С, є:

(15)

Отже, остаточно

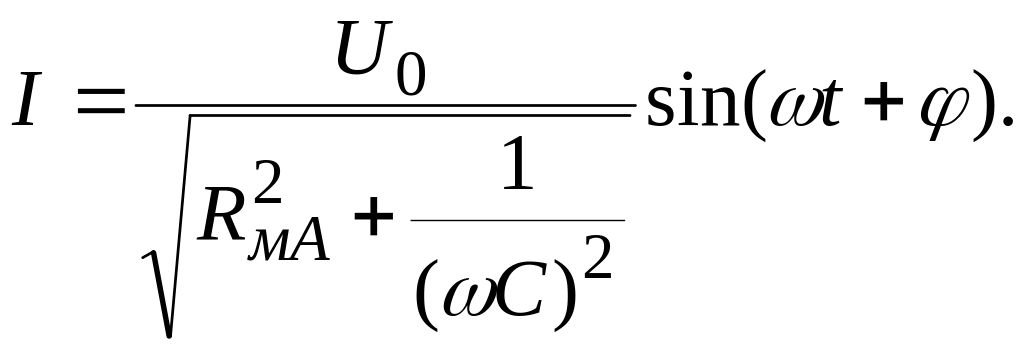(16)

Проаналізуємо останній вираз. Перше, що ми бачимо, це те, що амплітуда струму залежить як від R, так і від 1/(C). 1/C входить у формулу точно так, як і R. Тому 1/C називають ємнісним опором. Розмірність 1/C в системі СІ є Ом.

Це є закон Ома для кола, складеного з резистора і конденсатора і зображеного праворуч відносно штрихової лінії (рис. 5а).

Друге, що ми бачимо, це зсув фаз між напругою U (11) і струмом I (16). Струм випереджає напругу на кут  або на час t=/. Це подано на векторній діаграмі (рис. 6).

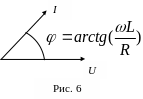
3. Розглянемо електричне коло, зображене на рис. 7а. Тут з джерелом змінного струму з’єднані послідовно реостат з опором R_р, котушка індуктивності L, конденсатор С і прилад для вимірювання сили струму (міліамперметр). Паралельно до котушки, конденсатора і приладу для вимірювання сили струму підключено прилад для вимірювання напруги (вольтметр). Еквівалентна схема електричного кола, зображеного на рис. 7а, наведена на рис. 7б. Вона відрізняється від схеми електричного кола на рис. 7а тим, що в ній явно представлено опір приладу для вимірювання сили струму (міліамперметра) і опір котушки. Знову ж таки, опір конденсатора є доволі малим і ним ми знехтували. Далі, як і в підрозділах 1, 2, будемо розглядати лише праву відносно штрихової лінії частину цього електричного кола.

Як і раніше, будемо вважати, що напруга у точках, до яких підключено вольтметр, змінюється у часі за законом.

(17)

Застосуємо до розглядуваного контуру друге правило Кірхгофа [6]:

(18)

Перший доданок – падіння напруги на резисторі R=R_L+R_мА. Напруга на конденсаторі де q – заряд конденсатора. Другий доданок у правій частині – це ЕРС самоіндукції (згідно з законом електромагнітної індукції Фарадея).

Підставляючи вираз для U_C у формулу (18), взявши від результату похідну за часом і врахувавши, що

,

одержимо:

Розділимо останнє рівняння на L. Одержимо:

(19)

Це також є лінійне неоднорідне диференціальне рівняння, але другого порядку. З наведеного вище, права частина диференціального рівняння є гармонічною функцією часу, рівняння лінійне, тому є сенс вважати, що і розв’язок рівняння буде гармонічною функцією часу. Тому приймаємо, що

де амплітуда струму I₀ і початкова фаза  підлягають визначенню.

Підставимо вираз для струму в диференціальне рівняння (19). Дістанемо

Розкриваємо косинус і синус суми аргументів і прирівнюємо множники при cos(t) і sin(t), оскільки ці функції є лінійно не залежними:

З другого рівняння знаходимо формулу для кута :

(20)

З першого рівняння знаходимо вираз для амплітуди струму

З рівняння (20) можна знайти cos і sin . Підставляючи їх в останню формулу, знаходимо амплітуду сили струму I₀

(21)

Отже, сила струму

(22)

Проаналізуємо останній вираз. Перше, що ми бачимо, це те, що амплітуда струму залежить як від R, так і від 1/( C) і від L. (1/C)–L входить у формулу точно так, як і R. Тому (1/C)–L називають реактивним опором послідовного з’єднання L і C і позначають також як Z. Розмірність (1/C)–L в системі СІ є Ом. Враховуючи, що R=R_L+ R_мА, запишемо

(23)

Отже, формула (22) – це закон Ома для кола, складеного з резистора, конденсатора і котушки індуктивності і зображеного праворуч відносно штрихової лінії (рис. 7а).

Друге, що ми бачимо, це те, що зсув фаз між напругою (17) і струмом (22) залежить від співвідношення між ємнісним і індуктивним опорами. Струм випереджає напругу, якщо 1/( C)>L (>0). При L>1/( C) струм відстає від напруги ( < 0).

При L=1/(C) зсув фаз дорівнює нулю. Реактивний опір, як це бачимо з формули (21) – (23) дорівнює нулю. Струм у колі досягає найбільшого значення. Його амплітуда

(24)

Це є резонанс.

З формули L=1/(C) випливає, що резонансу можна досягти, змінюючи L, C або . Частота, при якій настає резонанс, називається резонансною. Циклічна або колова резонансна частота

частота

(25)

а період

Останню формулу називають формулою Томсона. Її широко використовують у радіотехніці.

Сформулюємо основні особливості розглянутого резонансу:

1. зсув фаз між напругою і струмом дорівнює нулю;

2. повний опір кола мінімальний і дорівнює активному опору;

3. амплітуда струму має найбільше значення ;

4. амплітуда напруги на активному опорі дорівнює амплітуді прикладеної напруги; напруги на реактивних елементах мають протилежні фази і компенсуються (їхня сума, тобто напруга на послідовно включених котушці і конденсаторі дорівнює нулю);

5. потужність джерела струму передається тільки активному опору, корисна потужність змінного струму максимальна.

Резонанс у такому колі називають послідовним або резонансом струмів.