2.7 Параллельное соединение конденсатора с активно индуктивным токоприемником. Резонанс токов
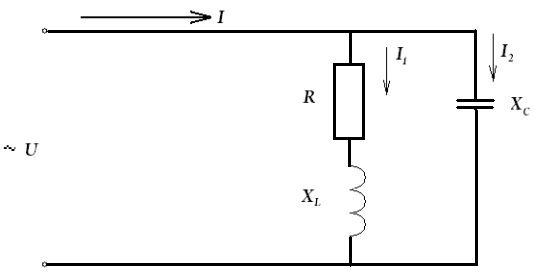
Рис. 2.36
В цепи (рис. 2.36) обе параллельные ветви находятся под одним и тем же приложенным напряжением U. Построим векторную диаграмму токов и напряжения.
Исходным вектором выберем вектор входного напряжения. Ток
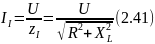
и отстает по фазе от напряжения на угол φ1:
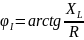(2.42)
Построенный
вектор тока
разложим на две составляющих IIR=IIcosφI
и IIL=IIsinφI
(рис. 2.37).
Рис. 2.37
Величину
вектора тока
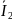определим из соотношения
.
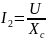Ток I2
опережает напряжение на
.
Ток в неразветвленной части цепи равен
векторной сумме:
(2.43)
Длина
вектора
(2.44)
Угол сдвига фаз между током в неразветвленной части цепи и напряжением:
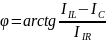(2.45)
Активную и реактивную составляющие тока II можно получить, зная проводимость первой ветви. Проводимость - величина, обратная сопротивлению
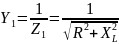(2.46)
Проводимость имеет активную и индуктивную составляющие. Легко показать:
активная
проводимость:
индуктивная
проводимость:
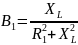(2.47)
Полная
проводимость первой ветви:
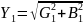(2.48)
Теперь
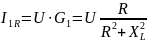(2.49)
(2.50)
Из векторной диаграммы видно, что длина и положение вектора тока I зависят от соотношения между реактивными токами I1L и Ic, а значит и от соотношения реактивных проводимостей.
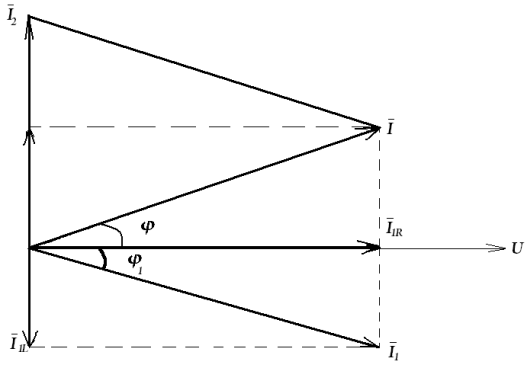
Рис. 2.38
При
I1L
> Ic
и В1
<B2=
.
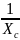Общий ток отстает по фазе от напряжения.
При I1L
< Ic
и В1
>B2,
ток опережает напряжение.
При равенстве реактивных проводимостей и, соответственно, реактивных токов I1L = Ic и В1 =B2 в цепи наступает резонанс токов (рис. 2.39).
Рис. 2.39
Ток в неразветвленной части цепи будет минимальным и равным активной составляющей тока I1, то есть для внешней цепи все процессы происходят так же, как если бы в цепь был включен только активный токоприемник.
Угол сдвига фаз между током I и напряжением U φ=0. В этом случае реактивные мощности Q1=U∙I1sinφ1 и Q2=U∙I∙sin параллельных ветвей одинаковы Q1=Q2 и взаимно компенсируют друг друга.
Этот режим используется в электрических цепях, питающихся активно-индуктивные токоприемники для компенсации реактивной мощности, т.к. позволяет увеличивать коэффициент мощности cosφ в питающей цепи.
Режим резонанса токов может быть получен изменением L, C или частотой ω из условия:
На практике рассчитывают емкость компенсационной батареи конденсаторов:
3. Трехфазные электрические цепи
3.1. Получение трехфазной системы эдс
Мы рассмотрели в 2.1. получение синусоидальной ЭДС путем вращения в магнитном поле проводника в виде рамки. Однако конструкция генератора может быть иной: когда магнит вращают вокруг катушки. Это удобнее, так как для присоединения цепи нагрузки не требуются контактные кольца.
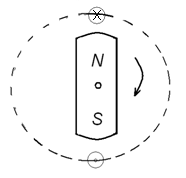
Рис 3.1 (a)
Если вместо одной взять три одинаковых обмотки и разместить их равномерно по окружности статора, то ЭДС индуцируются в каждой из обмоток (рис. 3.1 (а)).
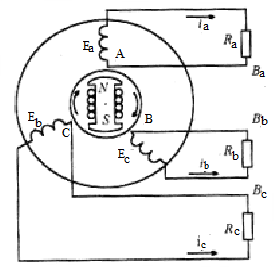
Рис. 3.1 (б)
Ось магнитного поля будет пересекать оси обмоток через одну треть периода вращения магнита, поэтому фазные ЭДС сдвинуты относительно друг друга на 1200.
Термин фаза имеет два значения:
Во-первых – это параметр синусоидального тока, напряжения, ЭДС;
Во-вторых – наименование одной из трех составных частей трехфазной цепи.
Трехфазный синхронный генератор, трехфазный синхронный и асинхронный двигатели, трехфазный трансформатор, а также трехфазные электрические цепи были изобретены М. О. Доливо-Добровольским в 1888-1891 годах, и достаточно быстро была распространена в мировой электротехнике благодаря своим достоинствам.
Временные и векторные диаграммы фазных ЭДС даны на рис. 3.2 (а и б- соответственно).
а)
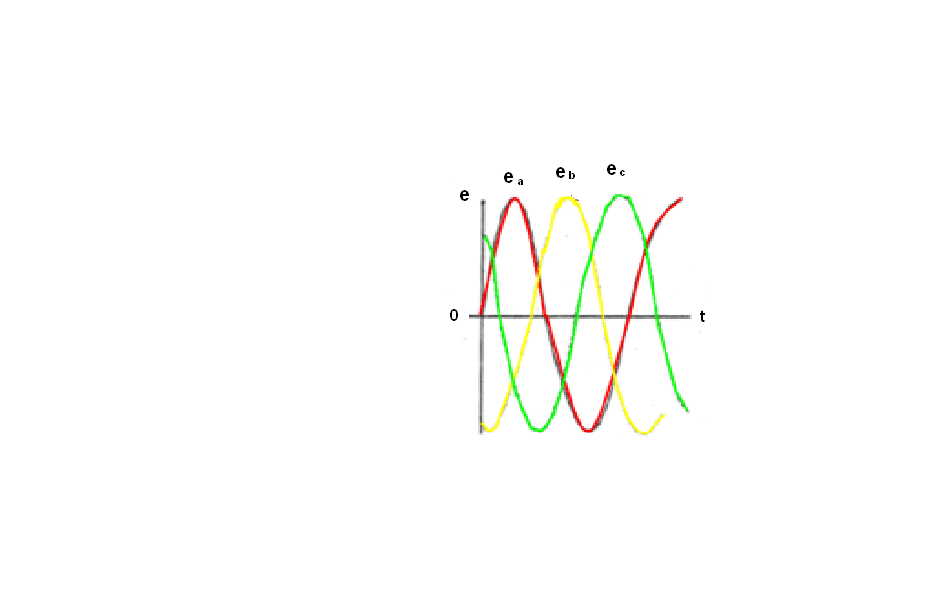б)
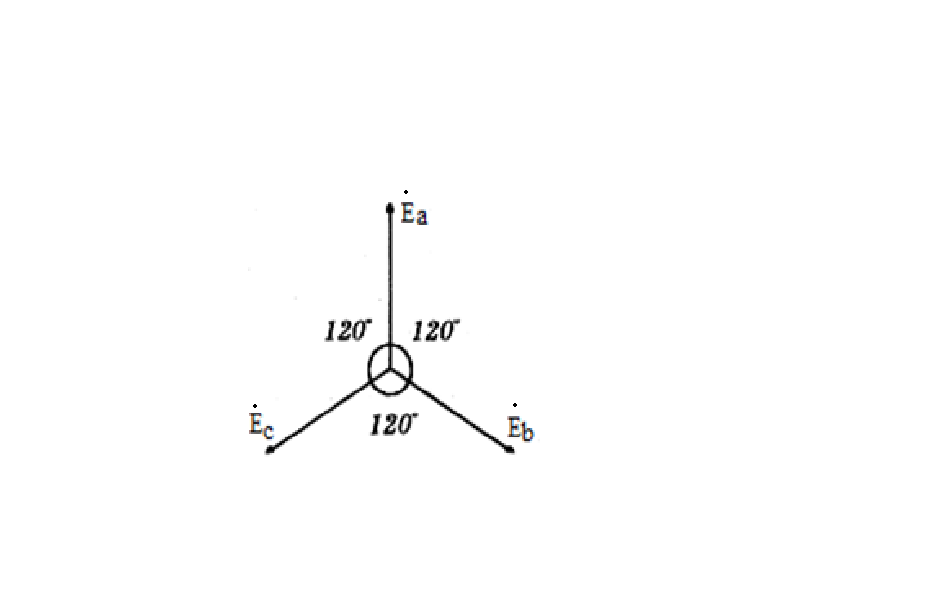
Рис. 3.2
Трехфазная система называется симметричной, если фазные ЭДС равны и нагрузка в фазах одинакова.
Мгновенные значения фазных ЭДС равны:
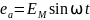
3.1
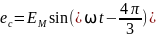
Комплексы действующих значений:
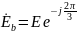3.2
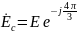
Если сложить в любой момент времени ЭДС (напряжения или токи), то получим замечательный результат: сумма фазных ЭДС:
3.3
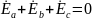3.4
В трехфазных системах применяется соединение обмоток звездой и треугольником (рис 3.3 а и б – соответственно).
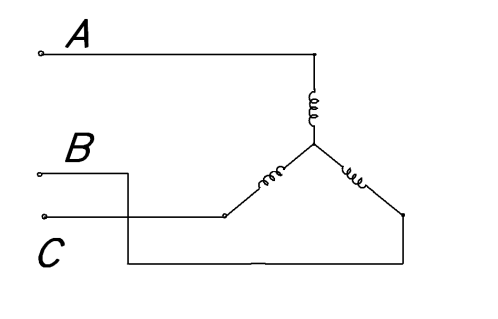
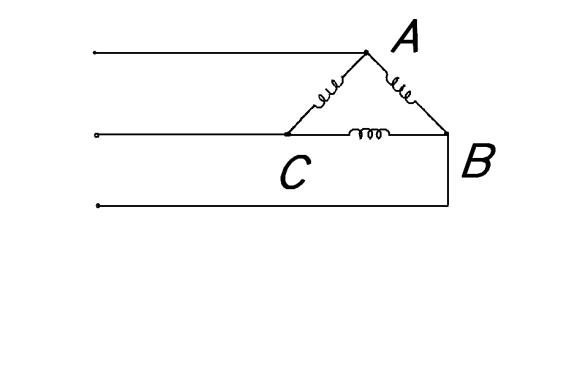
Рис 3.3 (а) Рис 3.3 (б)