2.5 Цепи синусоидального тока с активно-индуктивной нагрузкой

Большинство токоприемников имеют активно-индуктивный характер и имеют схему замещения, показанную на рис. 2.29. Рассмотрим основные соотношения в этой цепи для действующих значений токов и напряжений.

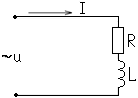
Рис. 2.29

Через индуктивный и активный элементы протекает один и тот же ток I. Определим напряжение на зажимах цепи, для чего определим падение напряжения на элементах, а входное напряжение определим по второму закону Кирхгофа:

(2.29)

Напряжение на активном элементе U_R=I∙R и совпадает по фазе с током (рис. 2.30).

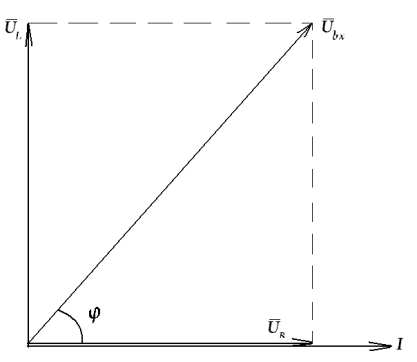
Рис. 2.30

Напряжение на индуктивности U_L=I∙x_L и опережает ток по фазе на . Вектор входного напряжения построим, складывая вектора U_L и U_R

Как видно из векторной диаграммы, модуль вектора 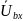равен:

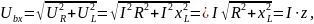(2.30)

где z - полное сопротивление цепи

(2.31)

Угол сдвига фаз между током и напряжением определим из векторной диаграммы:

Энергетический процесс в этом случае складывается из двух, рассмотренных выше. Часть электроэнергии, поступившей в цепь, преобразуется в другие виды, другой частью источник и индуктивный элемент периодически обмениваются.

Активная мощность Р характеризует процесс преобразования электроэнергии в другие виды:

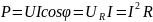(2.32)

Реактивная мощность - процесс обмена энергии между участком цепи и источником:

(2.33)

сosφ – коэффициент мощности. Является одним из показателей качества использования энергии: чем больше сosφ, тем больше количество энергии преобразуется в другие виды, т.е. тем лучше электроэнергия используется.

Произведение U·I=S (2.34) называют полной мощностью. Эта величина зачастую определяет эксплуатационные возможности электротехнических устройств (генераторов, трансформаторов, двигателей) и указывается в паспортных данных. Легко показать:

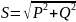(2.35)

Единицы измерения мощности P, Q, S одинаковы, но названы по-разному, чтобы показать разницу энергетических процессов, ими характеризуемых.

Активная мощность Р измеряется в Ваттах – Вт; реактивная мощность Q – в Варах (Вольт-Ампер реактивный); полная мощность S – в ВА (Вольт – Амперах).

2.6 Последовательная цепь r, l, c. Резонанс напряжений.

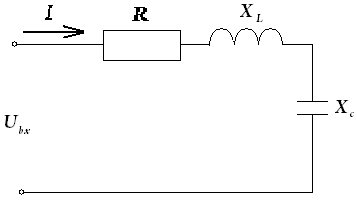
Рис. 2.31

В последовательной цепи через все элементы протекает один и тот же ток I, а входное напряжение найдем как сумму:

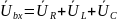, (2.36)

где U_R=IR и совпадает по фазе с током;

U_L=IХ_L и опережает ток на ;

U_C=IX_C и отстает от тока на .

Будем считать X_L>X_C, тогда векторная диаграмма соответствует рис. 2.32.

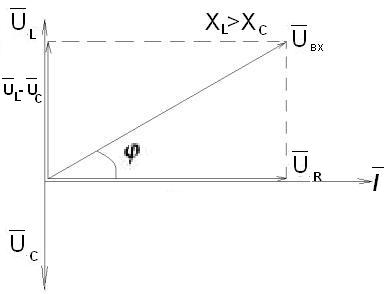
Рис. 2.32

Теперь можем определить модуль приложенного напряжения и сдвиг фаз между током и напряжением φ:

, (2.37)

где Z – полное сопротивление цепи.

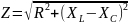(2.38)

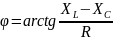(2.39)

Угол φ сдвига фаз между входным напряжением и током определяется соотношением реактивных сопротивлений. В данном случае угол φ >0, напряжение опережает ток по фазе.

При (рис. 2.33) напряжение по фазе отстает от тока и угол φ<0.

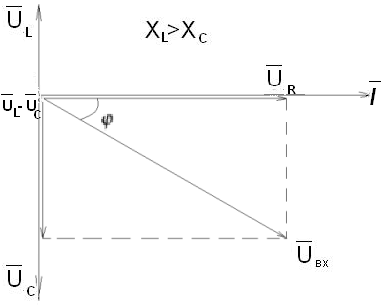
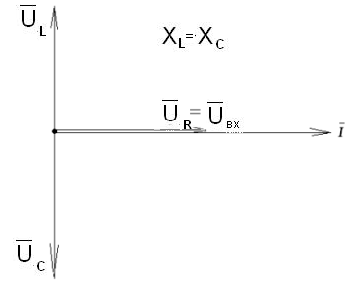
Рис. 2.33 Рис. 2.34

Из векторной диаграммы можно построить треугольник сопротивлений и треугольник мощностей, умножив соответствующее сопротивление на квадрат тока I².

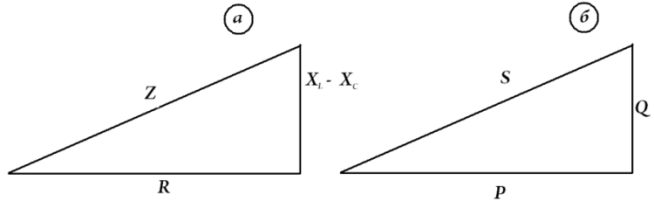
Рис.2.35

Из треугольника сопротивлений получим:

R=zcosφ; x=zsinφ.

Из треугольника мощностей:

P=Scosφ; Q=Ssinφ.

Особый интерес представляет режим работы последовательной цепи R, L, C, когда реактивные сопротивления равны между собой: X_L=X_C

В этом случае z=R.

Напряжения на индуктивности и на емкости находятся в противофазах и их сумма в любой момент времени равна нулю:

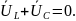
Входное напряжение равно напряжению на резистивном элементе.

Ток в цепи

- максимален и совпадает по фазе с напряжением. Напряжения на реактивных сопротивлениях при x_L=x_c>>R достигают больших значений, могут во много раз превышать входное напряжение.

Таким образом в цепи на отдельных участках могут возникать перенапряжения, опасные для изоляции.

Настроить цепь в резонанс напряжений, исходя из условия 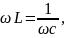можно изменением индуктивности L, емкости С или частоты ω. Частота при которой в цепи наступает резонанс напряжений называется резонансной ω:

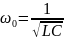(2.40)