2.2 Параметры переменного тока

Значение синусоидального тока в любой момент времени полностью характеризуется пятью параметрами: амплитудой, периодом, частотой, начальной фазой 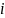и круговой частотой.

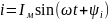(2.6)

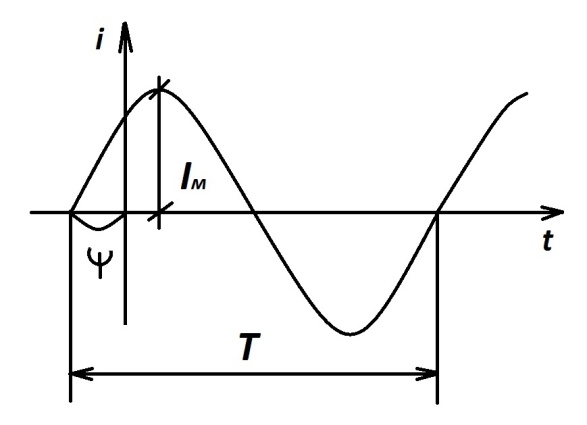
Рис.2.7

где 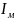- амплитуда тока определяет наибольшее отклонение заряженных частиц от положения равновесия;

T - период - время одного полного колебания;

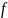- частота - количество полных колебаний, совершенных за одну секунду:

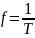(2.7)

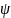- начальная фаза - определяет смещение синусоиды тока относительно начала координат, т.е. значение тока в нулевой момент времени;

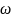- круговая частота тока;

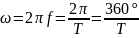(2.8) - определяет полный угол поворота рамки за период T. Аналогично току могут быть представлены мгновенные значения ЭДС и напряжения;

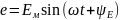
(2.9)

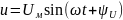
Для этих величин, характеризующих любой режим работы электрической цепи важно знать еще и действующее значение, которое определяют по тепловому действию переменного тока.

Значение постоянного тока, проходящего через одно и то же сопротивление в один и тот же промежуток времени, что и данный переменный ток, и выделяющего равное с ним количество теплоты называется действующим значением синусоидального тока.

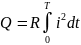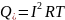, , отсюда

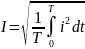(2.10)

Таким образом, действующее значение синусоидального тока определяется как среднее квадратичное за период.

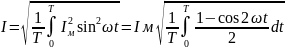
Т.к . 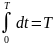и получим

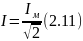
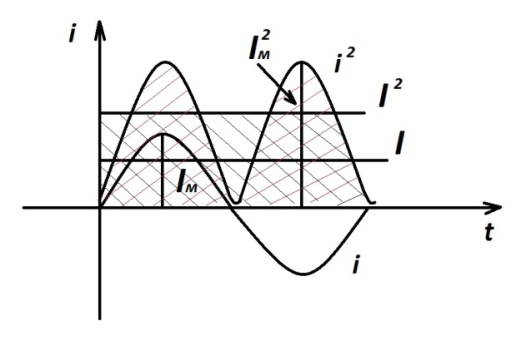
Рис.2.14

Аналогично, действующие значения ЭДС и напряжения:

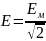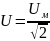; (2.12)

Действующие значения тока, напряжения, ЭДС выбраны в качестве основных, т.к. в большинстве случаев: действие тока пропорционально квадрату этого значения. Приборы, измеряющие значения электрических величин в цепях переменного тока, показывают действующие значения этих величин.

2.3 Векторные диаграммы

Переменный ток характеризуется двумя величинами - амплитудой и фазой .

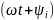Для математического описания переменного тока широко используется два метода: представление синусоизменяющихся величин вектором на плоскости или, для момента времени t=0, комплексными числами. Удобно строить векторные диаграммы. Вектор на плоскости имеет длину, равную максимальному или действующему значению тока, а угол наклона и горизонтальной оси - начальной фазе (рис.2.15).

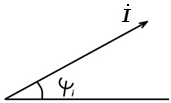
Рис.2.15

Комплексное число

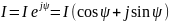(2.13)

имеет действительную и мнимую составляющие, а также модуль: 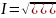, (рис.2.16)

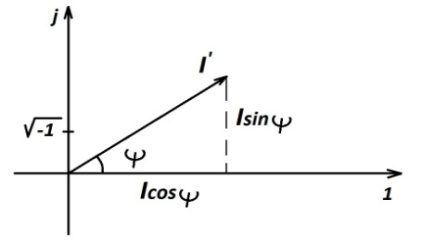
Рис.2.16

Применение векторных диаграмм позволяет упростить расчеты цепей синусоидального тока и получить наглядную картину количественных и фазовых соотношений электрических величин для данного режима.

2.4 Резистивный, индуктивный и емкостный элементы в цепях синусоидального тока

В любой электрической цепи может происходить три энергетических процесса:

• преобразование электрической энергии в другие виды (механическую, лучистую, тепловую);

• обмен электромагнитной энергией между магнитным полем индуктивного элемента и внешним усилием;

• обмен энергией между энергетическим полем конденсатора внешней цепью.

1. Активное сопротивление - параметр участка цепи, характеризующий способность участка цепи преобразовывать электромагнитную энергию в другие виды.

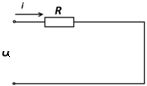
Рис.2.17

Рассмотрим цепь, содержащую активное сопротивление R. В цепи течет синусоидальный ток 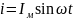. Согласно закону Ома:

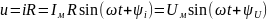(2.14)

Ток и напряжение совпадают по фазе. Это показано на временной (рис.2.18, а) и векторной (рис.2.18, б) диаграммах.

Мгновенная мощность - мгновенная скорость изменения энергии, всегда равна произведению мгновенных значений тока и напряжения:

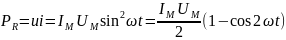(2.15)

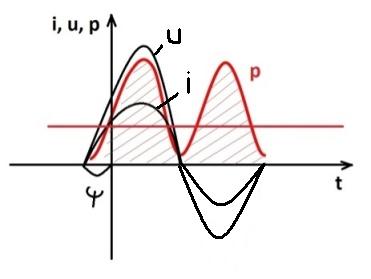
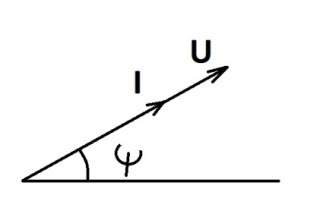
а) б)

Рис.2.18

Построив временную диаграмму мгновенной мощности, видим, что она всегда положительна. Это значит, что энергия всегда поступает в резистивный элемент из внешней цепи и преобразуется там в другие виды.

Активная мощность - среднее за период значение мгновенной мощности:

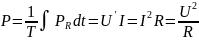(2.16)

2. Индуктивность - параметр, характеризующий способность участка цепи накопить магнитное поле:

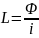
Измеряется в Генри 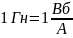, чаще принимают кратную единицу 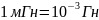. Один и тот же намагничивающий ток может создать разное по величине магнитное поле. Вокруг прямого тока (рис. 2.19, а) существует магнитное поле. Если проводник свернуть в контур - магнитное поле внутри него будет больше, чем у прямого тока (рис.2.19, б). В центре соленоида магнитное поле будет создано током во всех витках. Оно будет больше, чем в одном витке в W раз, где W - число витков. Если в соленоид вставить магнитный сердечник, магнитное поле усилится во много, раз за счет его внутренней намагниченности. Таким образом, индуктивность L зависит от конфигурации проводника с намагничивающим током, а так же от наличия магнитопровода.

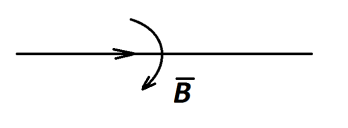
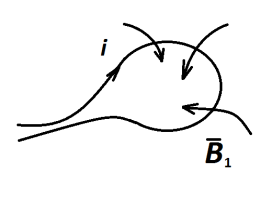
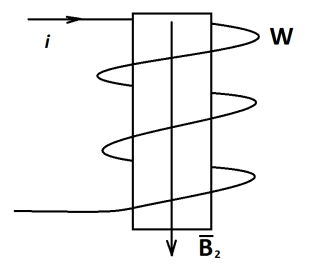
а) б) в)

Рис.2.19

Рассмотрим цепь, содержащую катушку индуктивности L без активного сопротивления (рис.2.20).

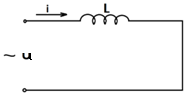
Рис.2.20

Ток, протекающий в ней , создает переменное магнитное поле, которое индуцирует в катушке ЭДС самоиндукции:

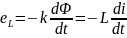(2.17)

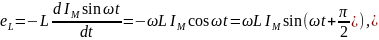(2.18)

Напряжение на индуктивности:

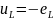
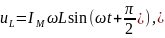
где 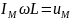- максимальное значение напряжения.

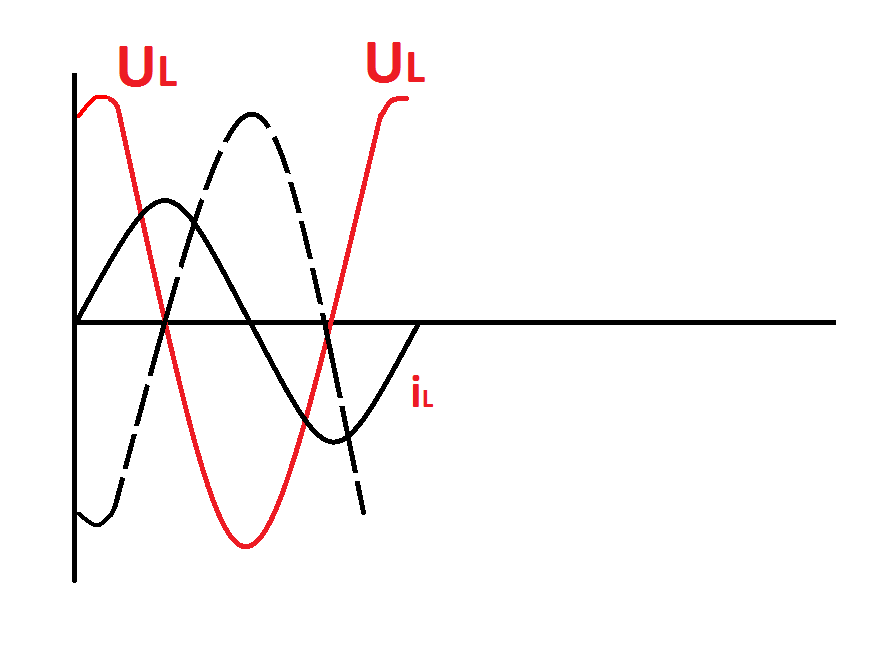
Рис.2.21

Временные диаграммы тока, ЭДС самоиндукции и напряжения показаны на рис.2.21.

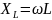- индуктивное сопротивление, имеет размерность - Ом, и как видно, пропорционально зависит от частоты. В цепи постоянного тока, при f=0, индуктивное сопротивление стремится к нулю, однако будет накоплена энергия:

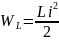(2.19).

Для действующих значений соотношения тока и напряжения:

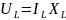(2.20)

На векторной диаграмме (рис.2.22) напряжение опережает ток на четверть периода.

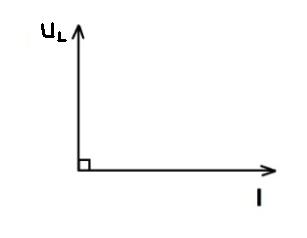
Рис.2.22

Мгновенная мощность

;

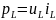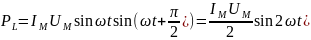(2.21)

изменяется с удвоенной частотой. В первой и третьей четвертях периода, когда ток возрастает по модулю, энергия поступает из внешней цепи в катушку индуктивности. Во второй и четвертой четвертях периода ток уменьшается, и энергия уходит из катушки во внешнюю цепь. Таким образом, происходит циклический обмен энергией между индуктивным элементом и внешней цепью.

Мощность, характеризующая такой процесс, называется реактивной, а индуктивный элемент - реактивным элементом.

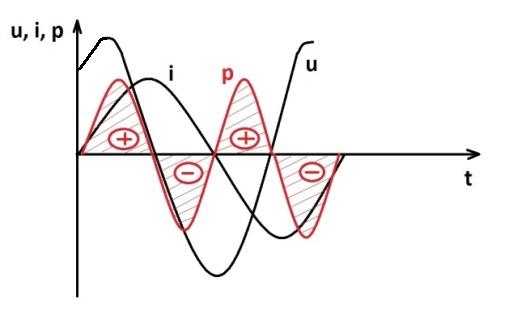
Рис.2.23

3. Электрическая емкость - параметр электрической цепи, характеризующий способность участка цепи накапливать электрическое поле. На пластинах плоского конденсатора накапливается заряд, пропорциональный приложенному напряжению. Это происходит за счет поляризации молекул диэлектрика, находящегося между пластинами конденсатора.

Рис.2.24

Величина этого заряда зависит от формы и размера пластины, а также расстояния между ними и от свойств диэлектрика:

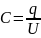(2.22)

Для плоского конденсатора:

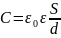(2.23)

где - электрическая постоянная: ;

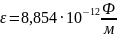𝜀 - относительная диэлектрическая проницаемость материала.

Измеряется емкость в Фарадах 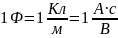, т.к. электрическая емкость в 1Ф очень велика, в электротехнике обычно используется дольные единицы емкости:

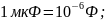
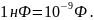
Рассмотрим электрическую цепь, содержащую конденсатор без активного сопротивления (рис.2.25), к которой приложено напряжение: .

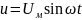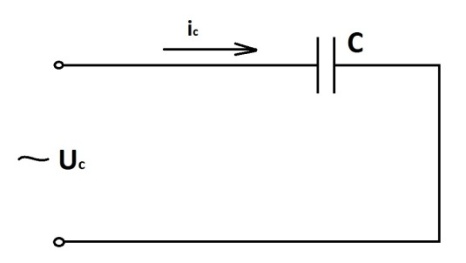
Рис.2.25

Мгновенное значение тока в этой цепи равно скорости изменения заряда на обкладках конденсатора:

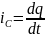(2.24)

Так как 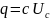, получим

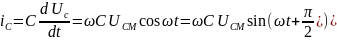(2.25)

где 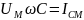- максимальное значение тока.

Ток на емкостном элементе определяет напряжение на четверть периода. Временные и векторные диаграммы тока и напряжения показаны на рис.2.26.

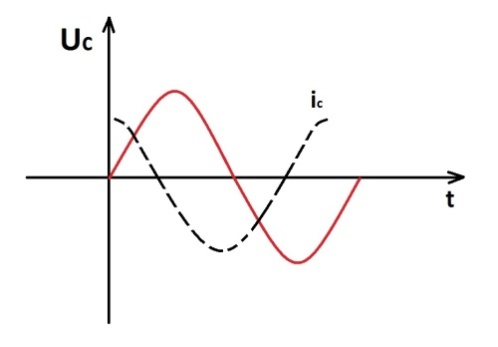
Рис.2.26

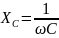- емкостное сопротивление, измеряемое в Ом, которое, как видно из формулы, обратно пропорционально частоте, т.е. при частоте f=0 - постоянный ток, сопротивление конденсатора бесконечно велико. Однако в нем будет накоплена энергия W_c :

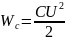(2.26)

Для действующих значений переменного тока получим:

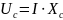(2.27)

Мгновенная мощность конденсатора:

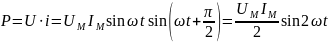(2.28)

Таким образом, мгновенная скорость изменяется с двойной частотой (рис. 2.27).

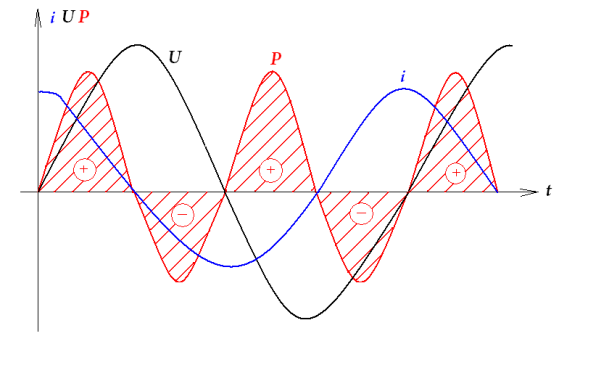
Рис. 2.28

При этом положительные значения мощности соответствуют заряду конденсатора (напряжение увеличивается по модулю), при отрицательных значениях мощности напряжение убывает, конденсатор разряжается.