1.4 Эквивалентные преобразования

Последовательным соединением элементов цепи называют такое, при котором конец предыдущего соединен с началом последующего. В одной точке последовательно могут быть соединены только два элемента.

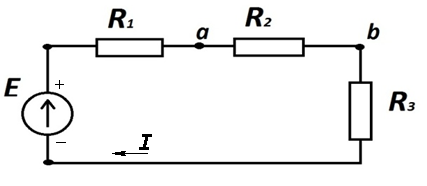
Рис.1.5

Ток в этом случае течет один и тот же на всех участках:

Если произвести эквивалентное преобразование трех резисторов одним с сопротивлением:

R_э= R₁+R₂+R₃ (1.10)

Ток в цепи не изменится. Т.е. при последовательном соединении элементов эквивалентное сопротивление равно сумме сопротивлений всех элементов цепи.

Параллельным соединением ветвей электрической цепи называют такое, когда начала всех ветвей собраны в один узел, а конец этих ветвей в другой (рис 1.6).

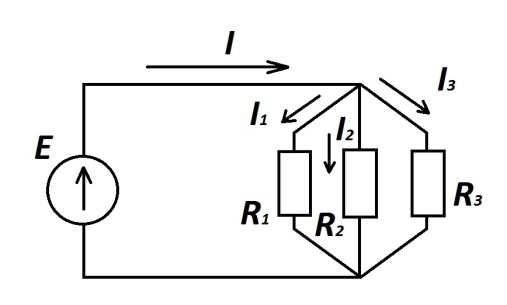
Рис.1.6

Напряжение на всех элементах одинаково и токи в них: 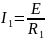; ; 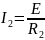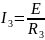. Ток в неразветвленной части цепи:

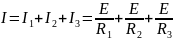или

Величина, обратная сопротивлению называется проводимостью: , измеряется в Сименсах: (1См = 1 Ом^-1).

Таким образом: I = E(G₁+G₂+G₃). Эквивалентное преобразование будет иметь место при замене трех параллельных ветвей – одной, с проводимостью:

G_э =G₁+G₂+G₃. (1.11)

Рассмотрим пример. В цепи на рис. 1.7. E = 60 В, R₁=3,6 Ом, R₂=6 Ом, R₃= 4 Ом.

Определить токи в ветвях, напряжение на зажимах параллельных ветвей U_ab. Составить уравнение баланса мощностей.

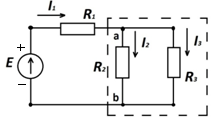
Рис. 1.7

Резисторы R₁и R₂соединены параллельно, их эквивалентная проводимость: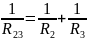 или . После преобразования цепь имеет вид (рис. 1.8):

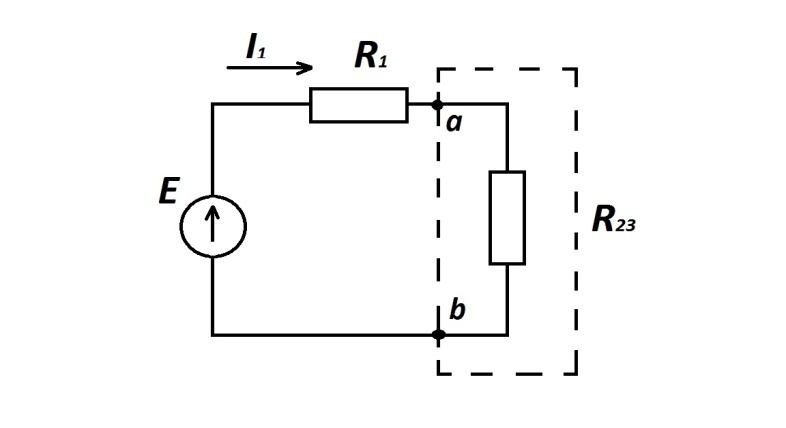
Рис.1.8

Резисторы R₁ и R₂₃ соединены последовательно. Эквивалентное сопротивление цепи: R_э = R₁+R₂₃ = 6 Ом.

Ток в неразветвленной части цепи: .

Ток в параллельных цепях обратно пропорционален сопротивлениям этих ветвей: .

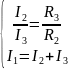Кроме того, решая эту систему уравнений, получим ;

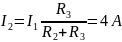
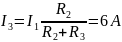
Уравнение баланса мощностей: .

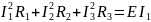1.5 Закон Кирхгофа

Два закона Густава Кирхгофа, открытые в 1845году, определяют параметры режима работы электрической цепи – ток I и напряжение U.

Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в одном узле электрической цепи равна нулю.

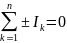, (1.12)

где n -число ветвей, сходящихся в узле.

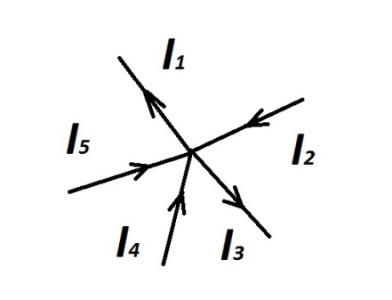
Рис.1.9

Токи, подтекающие к узлу и оттекающие от узла, в уравнения следует записывать с разными знаками. Для узла рис.1.9:

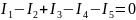
Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС, входящих в контур:

(1.13)

где m -число ветвей ,входящих в контур.

При составлении уравнения следует задаться положительным направлением обхода контура и направлением токов в ветвях.

Если направление стрелки тока или ЭДС совпадает с положительным направлением обхода контура, то падение напряжения или ЭДС записывают в уравнение со знаком «+».

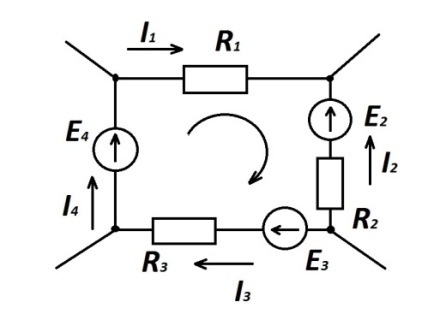
Рис. 1.10

Для контура рис.1.10:

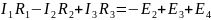
Используя закон Кирхгофа, можно рассчитать режим работы электрической цепи любой сложности. Общей задачей является расчет токов во всех ветвях электрической цепи при заданных сопротивлениях и ЭДС.

Если цепь содержит n узлов иm ветвей, то по первому закону можно составить (n−1) независимых уравнений, а по второму - столько, сколько независимых контуров содержит электрическая цепь. Независимым называется контур, в который входит хотя бы одна ветвь, не входящая в другие контуры. Число их в любой цепи m−(n−1).

Всего же система уравнений будет содержать столько уравнений, сколько ветвей содержит электрическая цепь.

Например, для цепи рис.1.11 можно составить три независимых уравнения:

Решив эту систему, получим токи во всех ветвях цепи. Правильность решения удобно проверить уравнением баланса мощности.

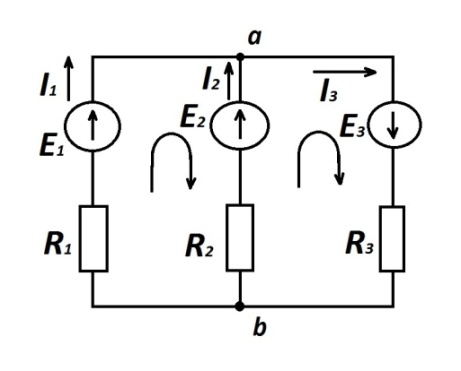
Рис.1.11