6 Пример решения задачи по определению коэффициента запаса для сосуда, работающего под давлением, с трещиной в стенке
6.1 Формулировка условия задачи
Определить запас прочности для цилиндрического сосуда, нагруженного при комнатной температуре внутренним давлением р. Нагрузка приложена статически. Сосуд изготовлен из стали, имеющей условный предел текучести 0,2 и предел прочности В.
При дефектоскопическом контроле на внутренней поверхности стенки сосуда обнаружена полуэллиптическая продольная трещина глубиной ℓ и протяженностью вдоль оси сосуда 2а.
6.2 Исходные данные для расчета приведены на рисунке 11.
Рисунок 11. Размеры сосуда и трещины на внутренней
поверхности стенки
Гипотеза прочности – III; внутреннее давление р =16 МПа; диаметр сосуда D = 0,52 м; толщина стенки сосуда H = 6,3 мм; глубина трещины в стенке сосуда ℓ = 2,8 мм; протяженность трещины 2а = 8,3 мм; сосуд изготовлен из стали, имеющей условный предел текучести σ0,2 = 622 МПа и предел прочности σВ = 950 МПа.
При испытании образца из той же стали, что и стенка сосуда с той же толщиной H = 6,3 мм и с шириной 2В = 40мм с центрально расположенной трещиной нормального отрыва длиной 2ℓобр. =8 мм разрушение произошло при номинальном разрушающем напряжении н =520 МПа.
6.3 Решение задачи
6.3.1 Определяем нормальные напряжения, действующие в стенке сосуда по формулам (3.1, 3.2):
окружные нормальные напряжения:
Меридиональные нормальные напряжения:
6.3.2 Определяем эквивалентные напряжения по значениям главных напряжений (3.4, 3.5) в соответствии с заданной третьей теорией прочности:
6.3.3 Определяем коэффициент интенсивности напряжений для материала сосуда КIc.
Коэффициент интенсивности напряжений определяется по результатам статических испытаний на растяжение при комнатной температуре плоских образцов (рисунок 12) из того же материала и той же толщины, что и стенка сосуда. Результаты эксперимента переносятся на основную конструкцию.
Рисунок 12. Образец с центрально расположенной трещиной нормального отрыва, нагруженный номинальными разрушающими напряжениями
В образцах шириной 2В выполняется центрально расположенная трещина нормального отрыва длиной 2ℓобр.. В данном примере указанные размеры заданы условием задачи.
По результатам испытаний (см. условие задачи) получено значение номинального разрушающего напряжения по минимальному сечению н = 520 МПа.
Разрушающее напряжение по неослабленному сечению (5.4):
Эффективную длину трещины в исследуемом образце ℓэфф.об. (см. рисунок 7) определяем по формуле (5.5), с учетом размеров пластической зоны в вершине трещины:
где – величина разрушающего напряжения по неослабленному сечению, определенная по формуле (5.4);
0,2 – условный предел текучести материала стенки сосуда.
Для пластины с центрально-расположенной трещиной поправочную функцию fIк об. определяем по формуле (5.6). Этой функцией учитываются условия нагружения и положение трещины в образце.
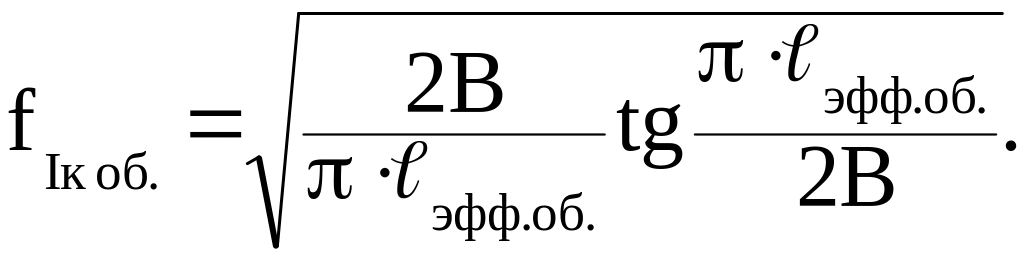
По формуле (5.3) рассчитываем коэффициент интенсивности напряжений К1с для материала, из которого изготовлен сосуд.
6.3.4 Определяем критическое (номинальное разрушающее напряжение) в стенке сосуда. Используем метод последовательных приближений.
Глубина трещины в стенке сосуда с учетом размеров пластической зоны в вершине трещины ℓэфф. неизвестна, поэтому расчет начинаем с определения этих напряжений по начальной глубине трещины ℓ = 2,8 мм и начальной длине трещины 2а = 8,3 мм.
Порядок расчета и расчетные формулы приведены в пп. 5.5 – 5.8.
В
соответствии с формулами 5.7 – 5.9, расчет
необходимо начинать с определения
коэффициента Ф0,
величина которого определяется по
графику, приведенному на рисунке 10 [1],
по отношению
Для найденного значения отношения глубины трещины ℓ к её полудлине а, равного 0,68 > 0,1 по графику (рисунок 13) Ф0 = 1,397.
На последующих этапах расчета величина Ф0 остается постоянной.
Рисунок 13. К определению значения функции Ф0
Для заданных условием задачи размеров и расположения трещины, а также толщины стенки сосуда Н = 6,3 мм, по формуле 5.8 определяем поправочную функцию:
Края трещины (стенка сосуда в месте разрушения) под действием внутреннего давления выгибаются наружу (см. рисунок 9).
Учитываем поправку на увеличение интенсивности напряжений при выгибании стенки сосуда при образовании сквозной трещины (см. формулу 5.9). Диаметр сосуда D = 0,52 м, толщина стенки Н = 6,3 мм.
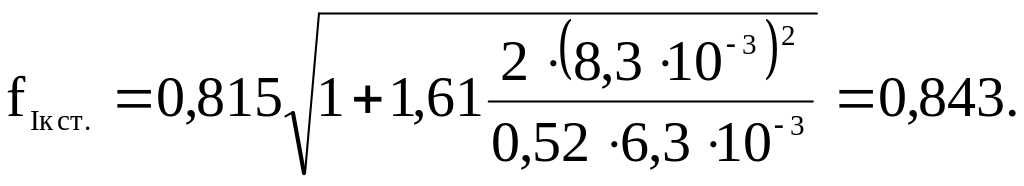
В случае, если 0,1 значение поправочной функции fIк = 1,12.
Значение критического коэффициента интенсивности напряжений материала сосуда КIс, полученное по результатам испытаний образца (п. 6.3.3), равно КIс = 52,92 МПа√м.
Определяем величину критического напряжения в стенке сосуда в соответствии с формулой 5.7.
где ℓ – глубина трещины в сосуде (задана по условию задачи);
fIк – поправочная функция.
Выполняем первое приближение в соответствии с п. 5.6. Полученное выше значение критического напряжения используем для определения глубины трещины с учетом пластической деформации в ее вершине (формула 5.10). Условный предел текучести материала стенки задан σ0,2 = 622 МПа.
Длина трещины в стенке возрастёт с тем же коэффициентом пропорциональности, что и глубина трещины:
В
формулу (5.12) подставляем найденное
значение
и определяем новое значение (в первом
приближении) поправочной функции:
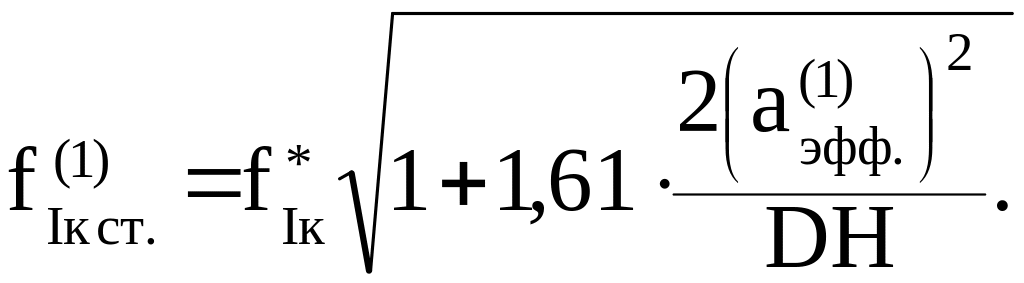
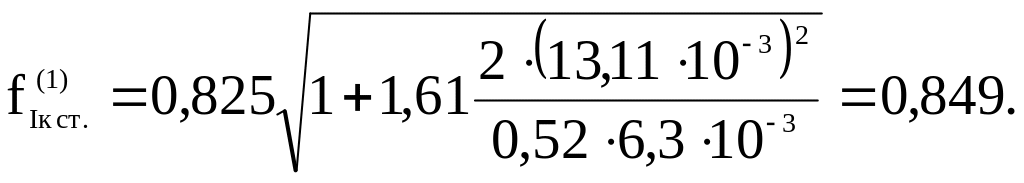
Величина критических (разрушающих) напряжений кр в первом приближении (5.13):
Выполняем второе приближение, повторяя расчеты по аналогии с первым приближением.
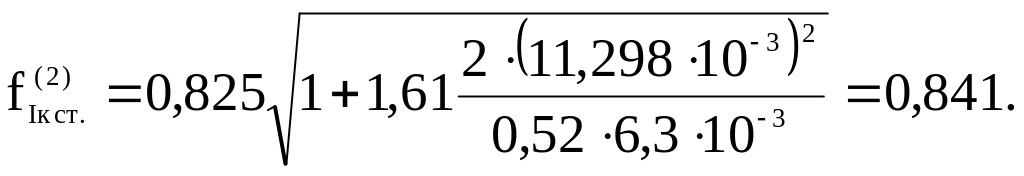
Определяем погрешность (процент расхождения) расчета критических напряжений:
Погрешность расчета
более 5%.
Выполняем третье приближение.
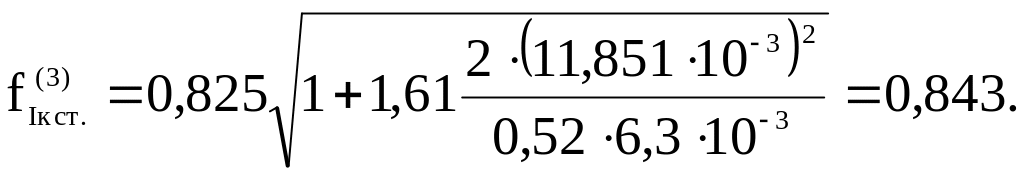
Определяем погрешность (процент расхождения) расчета критических напряжений:
Погрешность расчета
менее 5%.
6.3.5 Определяем коэффициент запаса для сосуда с трещиной в стенке по формуле (5.1)
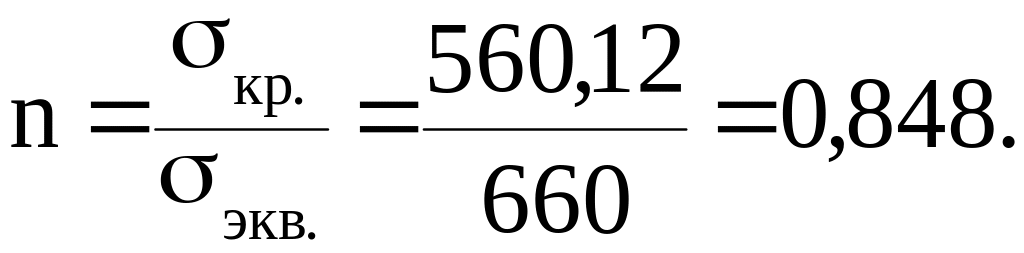
Коэффициент запаса меньше единицы, поэтому нагружение сосуда при заданных условием задачи исходных данных недопустимо.