§ 6. Параллельный перенос плоскости и пространства

п.1. Определение и свойства параллельного переноса

Параллельным переносом пространства (плоскости) на вектор называется отображение пространства (плоскости) на себя, при котором для всякой точки M и её образа выполняется равенство

(1)

Иначе говоря, все точки смещаются в одном и том же направлении на одно и то же расстояние. Часто параллельный перенос называют просто переносом.

Теорема 1. Параллельный перенос есть движение, сохраняющее направление.

Доказательство. Докажем, что параллельный перенос есть движение. Пусть произвольные точки A и B переходят в точки и (рис. 4). Тогда и из равенств

AB = AA + A B; AB = AB + BB

следует AB = AB.

Из этого равенства следует, во-первых, что AB=AB, т.е. что параллельный перенос является движением, и, во-вторых, что векторы AB и AB сонаправлены, т.е. что параллельный перенос сохраняет направление.

Нетрудно доказать, что движение, сохраняющее направление, есть перенос. Действительно, из равенства AB = AB следует, что AA = BB, т.е. что все точки переместились на один и тот же вектор AA = a. Доказанное свойство является признаком параллельного переноса.

Теорема 2. Композиция переносов есть перенос . Эта композиция коммутативна.

Доказательство. Пусть M – произвольная точка и

Тогда Так как , , то

, т.е. . Коммутативность композиции следует из коммутативности сложения векторов.

Теорема 3. Движение, обратное параллельному переносу на вектор , есть перенос на вектор .

Доказательство предоставляется читателю.

п.2. Аналитическое задание параллельного переноса

Теорема 1. В декартовой системе координат параллельный перенос на вектор (a₁, a₂, a₃) задаётся равенствами:

И обратно, всякая система вида (2) задаёт в декартовых координатах параллельный перенос на вектор (a₁, a₂, a₃).

Доказательство. Пусть точка O – начало координат, точка M(x, y, z) – образ точки M (x, y, z) при параллельном переносе на вектор . Тогда , откуда следуют равенства (2).

Пусть теперь точке M (x,y,z) сопоставляется точка M(x+a₁, y+a_2, z+a₃). Тогда = (a₁, a₂, a₃). Следовательно, равенства (2) задают параллельный перенос.

Из формул (2) видно, что параллельный перенос есть движение I рода, так как

§ 7. Поворот плоскости

п.1. Определение и аналитическое задание поворота плоскости

Неподвижной точкой преобразования называется точка, отображающаяся на себя.

Фигура (множество точек) называется неподвижной при данном преобразовании, если все её точки неподвижны.

Фигура называется инвариантной при данном преобразовании, если она содержит свой образ.

Например, при параллельном переносе на ненулевой вектор нет неподвижных точек; всякая прямая, параллельная вектору переноса, инвариантна.

Поворотом (вращением) плоскости вокруг точки О называется движение плоскости, при котором либо точка О является единственной неподвижной точкой (центром поворота), либо все точки неподвижны (тогда любая точка считается центром поворота).

Найдём формулы, задающие поворот в декартовых координатах. Известно (§ 4), что всякое движение задаётся одной из двух систем:

или

Выясним, какая из этих систем и при каких условиях задаёт поворот.

Чтобы найти неподвижные точки преобразования, заданного системой вида

x= f(x,y),

y= g (x,y),

нужно найти решения системы уравнений:

x= f(x,y),

y= g (x,y).

Для преобразования (1) получим систему уравнений:

x =x cos - y sin+a,

y = x sin + y cos+b

или:

(cos -1)x - y sin+a=0,

x sin + (cos-1)y+b=0 (3)

Вычислим определитель  системы уравнений (3):

Если  ≠ 0, то ∆ ≠ 0, система имеет единственное решение, а преобразование (1) является поворотом.

Если  = 0, a=b=0, то преобразование (1) является тождеством, а значит – поворотом.

Если  = 0 и a² + b² ≠ 0 (т.е. хотя бы одно из чисел a или b отлично от нуля), система уравнений (3) не имеет решений и преобразование (1) является параллельным переносом.

Рассмотрим преобразование (2). Система уравнений для отыскания неподвижных точек приводится к виду:

(cos -1)x + y sin+a=0,

x sin  - (cos +1)y+b=0. (4)

Вычислим определитель системы уравнений (4)

Это значит, что преобразование (2) либо не имеет неподвижных точек, либо их бесконечно много. Докажем, что преобразование (2) не является тождеством ни при каких значениях , a, b.

Действительно, если преобразование (2) является тождеством, то точки A(0,0), B(1,0), C(0,1) неподвижны. Из неподвижности точки A следует a=b=0 , из неподвижности точки B следует =0, из неподвижности точки C следует  = π. Таким образом, условия неподвижности точек A, B, C несовместны и преобразование (2) не является тождеством. Поскольку преобразование (2) не может иметь единственную неподвижную точку и не является тождеством, то оно не поворот.

Полученный результат можно сформулировать в виде следующей теоремы.

Теорема 1. Система (1) задаёт поворот плоскости при любых ,, a, b, кроме { = 0 и a² + b² ≠ 0}. Всякий поворот плоскости может быть задан в декартовых координатах системой вида (1).

Поскольку определитель системы (1) равен 1, то поворот есть движение первого рода.

п.2. Свойства поворота плоскости

Теорема 2. Для любого луча l с началом в центре поворота и его образа l угол (l,l) при данном повороте один и тот же.

Доказательство. Введём декартовы координаты с началом в точке O – центре поворота. Тогда в формулах (1), задающих поворот, a=b=0. Луч l зададим единичным направляющим вектором , координаты точки A обозначим (a₁, a₂), a₁²+a₂² =1. Через A (a₁,a₂), обозначим образ точки A, при этом a₁²+a₂² =1. По формулам (1) получим

a₁ =a₁ cos - a₂ sin,

a₂ = a₁ sin + a₂ cos .

Поэтому

cos(l,^{^}l)=cos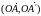 = =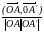 = a₁²cos  - a₁a₂sin +a₁a₂sin + a₂² cos  = cos .

Таким образом, все лучи с началом в центре поворота поворачиваются на один и тот же угол, что соответствует наглядному представлению о повороте плоскости. В дальнейшем удобно обозначать поворот с центром O на угол  символом R_O^.

Теорема 3. Композиция R_O^ R_O^, где  и  – ориентированные углы, есть поворот R_o^θ+φ. Эта композиция коммутативна.

Доказательство. За начало координат примем центр поворотов – точку O. Тогда повороты R_O^,и R_O^ задаются системами:

R_O^ : x =x cos - y sin

y = x sin + y cos (5)

R_O^ : x =x cos - y sin

y = x sin + y cos (6)

Подставляя в равенства (6) вместо x, y их значения, выраженные равенствами (5), получим:

R_O^ R_O^ : x =(x cos - y sin)cos - (x sin + y cos)sin

y =( x cos - y sin)sin + (x sin + y cos)cos

Из формул для синуса и косинуса суммы следует

x =x cos(+) - y sin(+)

y = x sin(+ )+ y cos(+) (7)

Коммутативность композиции очевидна.

Теорема 4. Для любых двух лучей l и m с общим началом O существует единственный поворот вокруг точки, отображающий луч l на луч m.

Доказательство. Примем за начало координат общее начало данных лучей, а за положительную полуось Ox – луч l. Угол (l,^ m) обозначим . Будем искать поворот R_O в виде

x =x cos - y sin

y = x sin + y cos (8)

Этот поворот будет определён, если мы найдем угол . Выберем на луче l точку A (1,0). При повороте на угол  она перейдёт в точку

A (cos, sin ). Из уравнений (8) получим: cos  =cos , sin =sin , т.е.  = и поворот определён однозначно.

Частным случаем поворота является центральная симметрия – поворот на угол . Очевидно, что центральную симметрию можно определить иначе: каждой точке M сопоставляется такая точка M, что выполняется равенство: .

В декартовых координатах симметрия относительно точки A(x₀, y₀) задаётся формулами:

x = -x +2x₀,

y = - y + 2y₀ , (9)

а если точка A совпадает с началом координат, то формулами

x = -x,

y = - y (10)

Симметрию относительно точки A будем обозначать Z_A.

Точка O называется центром симметрии фигуры, если при этой симметрии фигура переходит в себя (инвариантна относительно центральной симметрии). Например, окружность имеет единственный центр симметрии – центр окружности; любая точка прямой является её центром симметрии.

Задача. Дано преобразование плоскости

1.Докажите, что это поворот.

2.Найдите: а) его центр; б) обратное преобразование; в) образ и прообраз точки М (0,2); г) образ и прообраз прямой l: 2x – y - 3 = 0.

Решение.Так как и то это движение. Так как , то это движение 1 рода. А так как это не параллельный перенос, то это – поворот.

1. а) Центром поворота является его неподвижная точка, т.е. та, для которой выполняются равенства: x = x, y = y. Поэтому

Решая эту систему, находим неподвижную точку – центр поворота – С(1,2).

б) Обратное преобразование. Пользуясь способом, указанным в §4, зададим обратное движение f ^–1 системой

Полагая (x,y)=(0,0), получим (x`,y`)= откуда

Обратное движение f ^–1 задаётся системой:

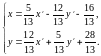
Замечание. Формулы преобразования f ^–1 можно получить иначе.

Движение f есть поворот вокруг точки С(1, 2) на угол Обратное движение есть поворот вокруг точки С на угол (-φ). Для любой точки M (x,y) вектор при повороте f ^–1 поворачивается на угол (-φ). Обозначим f ^–1(M)=M(x, y). Координаты вектора преобразуются по формулам:

в) Координаты образа и прообраза точки М (0,2) получаются при подстановке координат точки М соответственно в системы уравнений, задающих движения f и f ^–1. Это точки и

г) Пусть фигура Q задана уравнением

F(x,y) = 0 .

Чтобы найти уравнение образа f(Q) фигуры Q, нужно установить зависимость между координатами точек M'(x,y) и точек M(x,y) при условии, что M' – образы точек М, принадлежащих фигуре Q. Поэтому нужно выразить x и y через x и y подставить в уравнение F(x,y) = 0 .

Уравнение прообраза фигуры Q получится, если подставить в уравнение фигур Q вместо (x,y) соответственно (x,y), выраженные системой, задающей данное движение.

Уравнение образа прямой l 2x – y + 3 = 0:

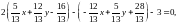
После упрощения получим:

f (l): 22x + 19y - 99=0.

Уравнение прообраза прямой l:

После упрощения получим:

f ^–1 ( l ): 2x + 29y + 21=0.