4. Изображение фигур в параллельной проекции.

Параллельное проектирование

4.1. Какие фигуры могут быть спроектированы а) в отрезок; б) в луч; в) в треугольник; г) в параллелограмм; д) в трапецию?

4.2. Докажите, что две взаимно перпендикулярные прямые, вообще говоря, проектируются не во взаимно перпендикулярные прямые.

4.3. Докажите, что параллельное проектирование, вообще говоря, не сохраняет а) расстояние между точками; б) величину угла; в) равенство отрезков; г) равенство углов.

4.4. Сохраняются ли при параллельном проектировании следующие свойства фигур: а) центральная симметричность; б) симметричность относительно прямой; в) выпуклость?

4.5. Найдите ошибку в рассуждениях: «Всякий параллелограмм может быть спроектирован в четырехугольник произвольной формы. Докажем это. Пусть АВСD - параллелограмм, А₁В₁С₁D₁ - плоский четырехугольник. Разобьем АВСD и А₁В₁С₁D₁ диагоналями ВD и В₁D₁ соответственно. Мы знаем, что треугольник АВD может быть спроектирован в треугольник произвольной формы, в том числе и треугольник, подобный треугольнику А₁В₁D₁, а треугольник ВСD - в треугольник, подобный В₁С₁D₁. Таким образом, параллелограмм АВСD может быть спроектирован в четырехугольник, подобный А₁В₁С₁D₁.»

4.5. Каково может быть взаимное расположение проекций двух скрещивающихся прямых на плоскость?

4.6. Известно, что А₁,B₁,С₁,D₁ - проекции точек А, В, С, D на плоскость . Определите по рисунку 39, является ли четырехугольник АВСD плоским.

4.7. Является ли прямой такая линия, у которой прямой является проекция а) на одну плоскость; б) на каждую из двух данных плоскостей (рассмотрите различные случаи расположения этих плоскостей)?

4.8. Даны два четырёхугольника АВСD и А₁В₁С₁D₁, не лежащие в одной плоскости, такие, что АО:ОС = А₁О₁:О₁С₁ и ВО:ОD = В₁О₁:О₁D₁ (О и О₁ - точки пересечения диагоналей АВСD и А₁В₁С₁D₁ соответственно). Докажите, что один из этих четырёхугольников подобен некоторой параллельной проекции другого на плоскость первого.

Изображение плоских фигур.

4.9. На изображении квадрата АВСD постройте изображения перпендикуляров, опущенных из середины Е стороны ВС на прямые ВD, АС, АN и DM, где M и N - середины сторон АВ и СD соответственно.

4.10. Дано изображение равнобедренного треугольника, высота которого равна основанию. Изобразите высоты этого треугольника и центр описанного круга.

4.11. Дано изображение прямоугольного треугольника с отношением катетов 3:4. Постройте изображение центров вписанной и описанной окружности.

4.12. Дано изображение окружности. Постройте изображение хорды, стягивающей дугу в α градусов (α = 90^о, 120^о, 60^о, 30^о, 45^о).

4.13. Дано изображение окружности. Постройте изображение прямоугольного треугольника, вписанного в эту окружность и имеющего угол 30^о.

4.14. Дано изображение окружности. Изобразите правильный треугольник, а) вписанный в эту окружность; б) описанный вокруг этой окружности.

4.15. Дано изображение окружности. Изобразите квадрат, а) вписанный в эту окружность; б) описанный вокруг этой окружности.

4.16. Дано изображение окружности. Изобразите правильный шестиугольник, а) вписанный в эту окружность; б) описанный вокруг этой окружности.

4.17. Дано изображение правильного треугольника ABC. Изобразите перпендикуляры, опущенные из середины F стороны AB на прямые AB и BC, на высоты AD и BE.

4.18. На изображении прямоугольного треугольника с острым углом 60° постройте изображение биссектрис внутреннего и внешнего углов при вершине этого острого угла.

4.19. На изображении прямоугольника ABCD с отношением сторон BC:CD = 2 постройте изображение а) перпендикуляра, опущенного из вершины C на диагональ BD; б) биссектрис внутренних углов при вершинах C и D.

4.20. Дано изображение равнобедренного прямоугольного треугольника. Изобразите квадраты, построенные на его сторонах.

4.21. Дано изображение квадрата. Изобразите правильный треугольник, построенный а) на стороне этого квадрата; б) на его диагонали.

4.22. Дано изображение правильного треугольника. Постройте изображения квадратов, построенных на сторонах этого треугольника.

4.23. Дано изображение правильного треугольника. Изобразите квадрат, вписанный в этот треугольник.

4.24. Дано изображение прямоугольного треугольника с углом 60°. Изобразите квадраты, построенные на его сторонах.

4.25. Дано изображение равнобедренного треугольника, высота которого равна основанию. Изобразите высоты этого треугольника и центр описанного круга.

4.26. Дано изображение прямоугольного треугольника с отношением катетов 3:4. Постройте изображение центров вписанной и описанной окружностей.

4.27. Дано изображение ромба с углом 60°. Изобразите правильный треугольник, построенный на его высоте.

4.28. Дано изображение прямоугольного треугольника с углом при основании, равным 30°. Изобразите биссектрисы внутреннего и внешнего углов при основании треугольника.

4.29. Дано изображение равнобедренного треугольника, основание которого в три раза меньше боковой стороны. Изобразите его медианы, биссектрисы, высоты.

4.30. Дано изображение треугольника, стороны которого относятся как 2:4:5. Изобразите высоты треугольника.

4.31. Дано изображение окружности. Изобразите два взаимно перпендикулярных диаметра этой окружности.

4.32. Дано изображение окружности. Постройте изображение прямоугольного треугольника, вписанного в эту окружность и имеющего угол 30°.

Изображение пространственных фигур.

4.34. На рисунке изображены некоторые многогранники и круглые тела. Некоторые из этих изображений неверные. Объясните, почему. Какие из них являются правдоподобными?

4.35. Изобразите куб так, чтобы ни одно из его рёбер не было изображено вертикальным отрезком.

4.36. Изобразите правильную треугольную пирамиду так, чтобы одно из его боковых рёбер было изображено горизонтальным отрезком.

4.37. Изобразите правильную четырёхугольную пирамиду и какой-нибудь прямоугольный параллелепипед, вписанный в эту пирамиду.

4.38. Изобразите сферу и какую-нибудь четырёхугольную пирамиду, вписанную в неё.

4.39. Изобразите сферу и какой-нибудь прямоугольный параллелепипед, вписанный в эту сферу.

Ответы

1.17. Гипербола.

1.18. Эллипс.

1.19. Пустое множество.

1.20. Парабола.

1.21. Парабола.

1.22. Две параллельные прямые.

2.1.

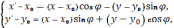
2.2.

2.3.

2.4.

2.5. Осевая или скользящая симметрия

2.6.

2.7. а) (5,0), (1,2); б) таких точек нет; в) x-2y = -11 ; г) д) параллельный перенос на вектор (2,-1);

е)

2.8. а) (-2,2), (8,-6); б) нет; в) x = -5, x = 5; г) 4x + 5y + c = 0; д) параллельный перенос на вектор (-5,4); е) x = x+5, y = y-4.

2.9. а) (1,2), (3,2); б) С (1,2); в) y = 1, y = 3; г) нет; д) ; е) x = y-1, y = -x+3.

2.10. а) (-1,-3), (-3,5), б) С(-2,1), в) x-2y = 3, г) нет; д) ; е) x = y-1, y = x+3.

2.11. а) (2,-2), (14/13,34/13); б) С(5/2,1/2); в) 12x-5y = 34, 12x+5y = 14; г) нет;

д) ,tg=-12/5;е)x=(5/13)+(12/13)+(14/13),y=(-2/13)x+(5/13)y+34/13.

2.12. a) (2,9), (-2,-1); б) С(-5/2, 5/2); в) 7x-y-5 = 0, x-7y-5 = 0; г) нет; д) , tg = 3/4; е) x = 4/5x+3/5y-2, y = (-3/5)x+4/5y-1.

2.13. a) (1,-2), (1,2); б) C(5/2,0); в) 4x – 3y -10 = 0, 4x + 3y – 10 = 0; г) нет; д) , tg = 4/3; е) x = (3/5)x + (4/5)y +1, y = (-4/5)x + (3/5)y + 2.

2.14. а) (-7/13, 17/13), (17/13, -7/13); б) О(0,0); в) 5x + 12 y = 13, 5x - 12y=13;

г) нет; д) , tg = 12/5; е) x = (5/13)x + (12/13)y, y = (-12/13)x + (5/13)y.

2.15. а) (-3,-2), (-3,-2); б) С(1,2); в) x-y = -2, x-y = -2; г) Ax+By-A-2B = 0; д) ; е) x = -x+2, y = -y+4.

2.16. а) (4/5, 12/5), (12/5,4/5); б) С(1,1); в) 4x-3y-6 = 0, 4x-3y-2 = 0; г) нет; д) , tg = -4/3; е) x = (-3/5)x-(4/5)y+12/5, y = (4/5)x-(3/5)y+4/5.

2.17. а) (1,2), (1,2); б) y = x; в) x-3y-5 = 0, x-3y-5 = 0; г) y=x, x+y = C; д) S_p, p: y=x;

е) x = y, y = x.

2.18. а) (5/13,12/13), (5/13,12/13); б) 2x-3y = 0; в)9x -46y = 0, 9x -46y = 0; г) 2x-3y = 0, 3x+2y = C; д) S_p, p: 2x-3y=0; е) x = (5/13)x+(12/13)y, y = (12/13)x-(5/13)y.

2.19. а) (-2,3), (-2,3); б) 4x+6y -13 = 0; в) 5x+12y = 39, 5x+12y = 39; г)4x-6y+13 = 0, 3x+2y+C = 0;д) S_p, p: 4x-6y+13 = 0;е) x = (5/13)x+(12/13)y-2, y = (12/13)x-(5/13)y+3.

2.20 a) (-1,-3), (-1,-3); б) y = - x; в) x = 0, х = 0; г) х+у = 0, х-у+С = 0; д) S_p, p: y = -x; e) x = -y, y = -x.

2.21 а) (3,-3), (3,-3); б) х-у = 2; в) 2х+у-2 = 0, 2х+у-2 = 0; г) х-у-2 = 0, х+у+С = 0; д) S_p, p: х-у-2 = 0; е) х = у+2, у = х-2.

2.22 а) , ; б) х-2у = 0; в) 7х+у = 0, 7х+у = 0; г) х-2у = 0, 2х+у = С; д) S_p, p: х=2у; е)

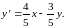
2.23 а) (-2,-7), (-2,-7); б) х+3у+8 = 0; в) 4х-3у = 8, 4х-3у = 8; г) х+3у+8 = 0, 3х-y+С = 0; д) S_p, p: х+3у+8 = 0; е) , .

2.24 а) (-4,-3), (-4,5); б) нет; в) 4х+3у+24 = 0, 4х = - 3у, г) 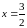; д) S_p,_a, р: , a(0,-4); e) x = -x+3, y = y+4.

1 Напомним, что ортоцентр треугольника – это точка пересечения прямых, содержащих его высоты.