С.А.Франгулов, Т.Г.Ходот

Преобразования плоскости и пространства

(учебное пособие для студентов педагогических вузов)

2012

Предисловие

В настоящем учебном пособии рассматриваются часто встречающиеся в разных областях математики и естественных наук линейные преобразования плоскости и пространства (преобразования, которые могут быть заданы в декартовых координатах линейными системами) и связанный с ними метод изображения на плоскости плоских и пространственных фигур при помощи параллельного проектирования.

Основным методом изучения преобразований плоскости и пространcтва в этом пособии является метод координат. При этом удобно во многих случаях при решении задачи применять разные системы координат. Поэтому необходимо уметь переходить от одной системы координат к другой, т.е. знать формулы перехода (преобразования) координат.

Следует иметь в виду, что слово «преобразование» употребляется здесь в разных смыслах.

В первом случае (§ 1.Преобразование декартовой системы координат) на плоскости введены две системы координат и ставится задача: зная координаты любой точки в одной системе, найти координаты этой точки в другой системе. Результаты § 1 применяются в § 2 к исследованию квадрик на плоскости.

Во втором случае слово «преобразование» означает отображение множества на себя. Преобразованиями в этом смысле являются рассматриваемые здесь движения, подобия, аффинные преобразования. Преобразования координат являются одним из способов изучения указанных отображений.

§ 1. Преобразования декартовых координат

Пусть в пространстве даны две декартовы системы координат, одну из которых будем называть старой, а другую – новой. Начало новой системы координат обозначим через O, базисные векторы – через , координаты произвольной точки в этой системе – через (x, y, z). Соответствующие элементы новой системы обозначим соответственно через O', , (x', y', z'). Надо, зная координаты точки в одной системе, найти её координаты в другой.

Эту задачу будем решать в два этапа: 1. Системы координат имеют общий базис и разные начала. 2. Системы координат имеют общее начало и разные базисы.3.Общий случай: и начала, и базисы систем координат различаются.

п. 1. Параллельный перенос осей

Будем говорить, что новая система получена параллельным переносом старой, если они имеют общий базис, то есть если направления старых и соответствующих новых осей совпадают.

Обозначим координаты точки O' относительно старой системы координат через (a, b, c). Поскольку базисные векторы обеих систем совпадают, то соответствующие координаты всякого вектора в обеих системах одни и те же.

Рассмотрим произвольную точку M. Её радиус-вектор в старой системе координат есть вектор (x, y, z), а в новой системе - 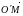(x', y', z'). Так как имеет место равенство:

,

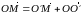где вектор имеет координаты (a, b, c), то зависимость между старыми и новыми координатами точки M имеет вид:

x = x'+a, y= y'+b, z= z'+ c. (1)

Формулы параллельного переноса осей на плоскости имеют вид:

x = x'+a, y= y'+b. (2)

В качестве примера использования полученных формул докажем, что график квадратного трёхчлена y = Ax²+Bx+C есть парабола.

Для этого выполним следующие тождественные преобразования:

y = A(x²+xB/A)+ C= = A(x²+xB/A+B²/4A²)+ C- B²/4A.

В результате получаем:

y – (C- B²/4A) = A(x +B/2A)² (3)