1. 1. Кинематика поступательного движения материальной точки и твердого тела.

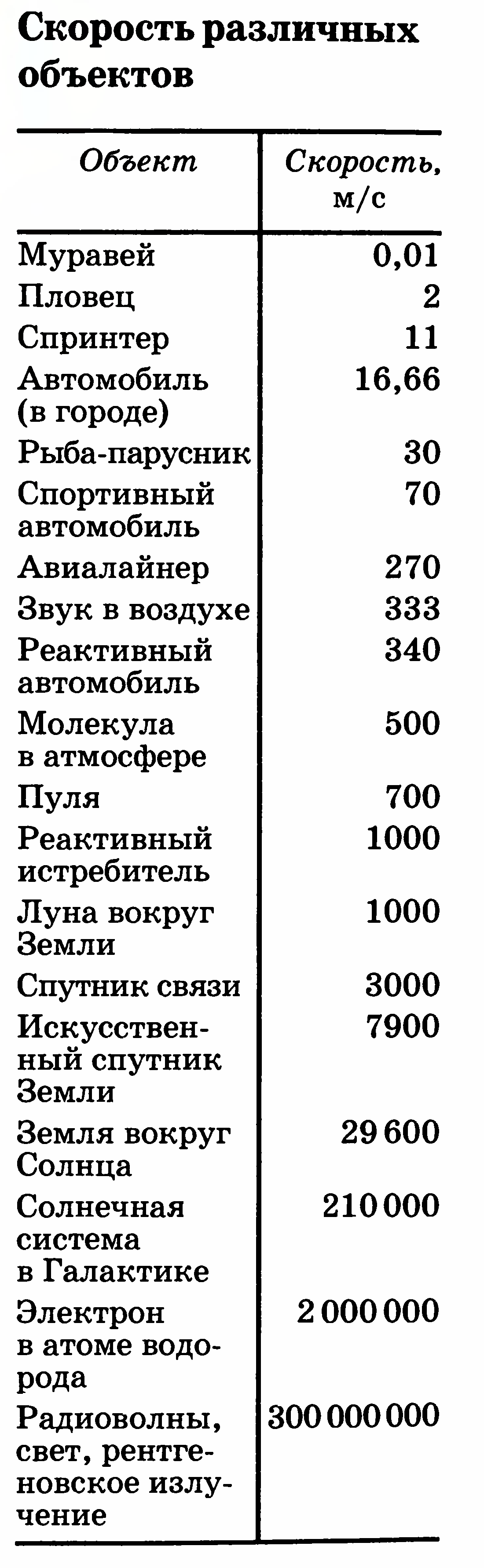
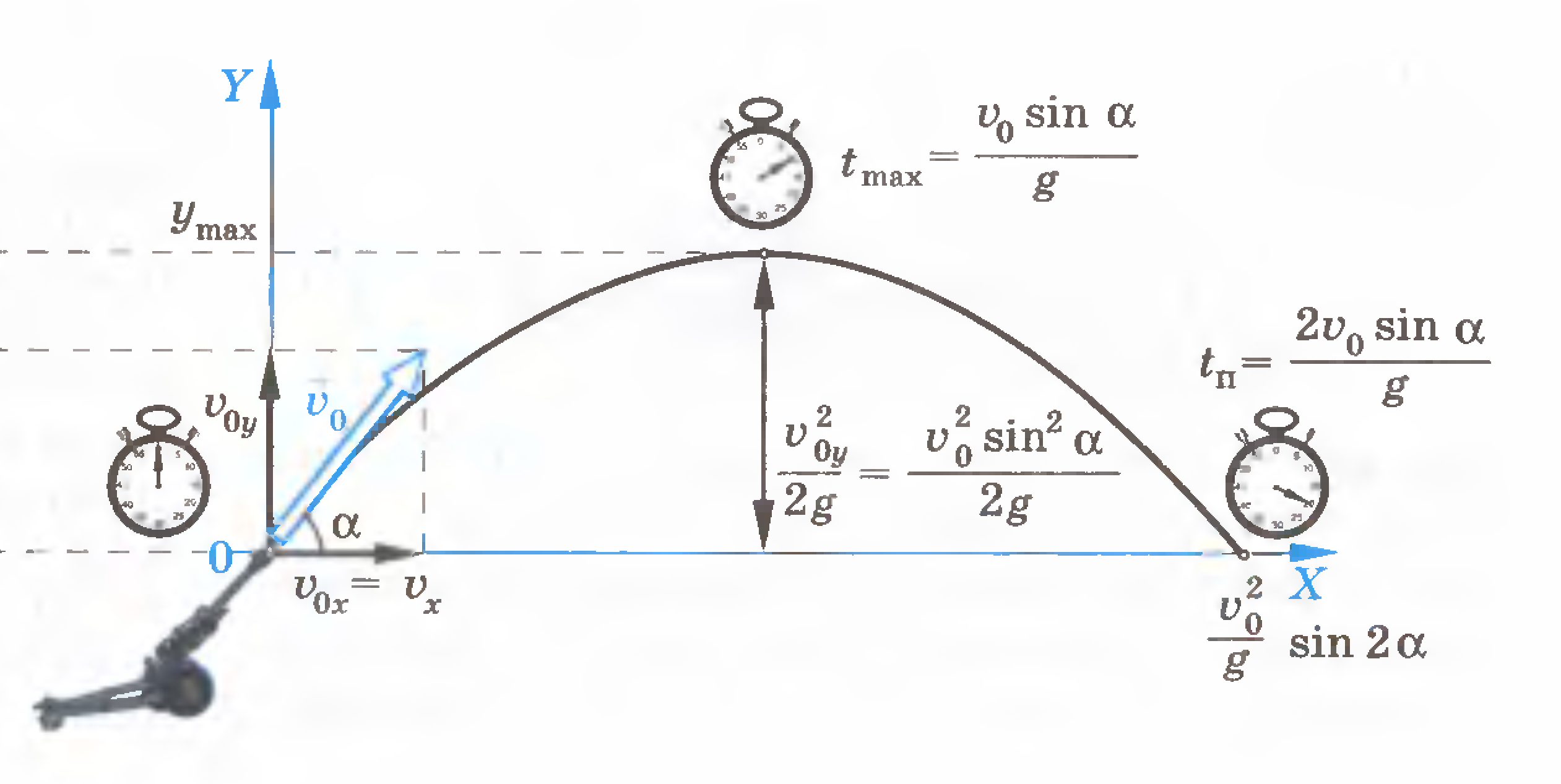
Понятия кинематики: материальная точка, траектория, путь, перемещение, уравнение движения. Способы задания уравнений движения. Скорость. Ускорение. Тангенциальное и нормальное ускорения.

Способы задания движения.

Скорость и ускорение.

1. Координатный способ – задаётся система координат X,O,Y,Z и точка, которая движется.

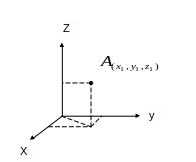
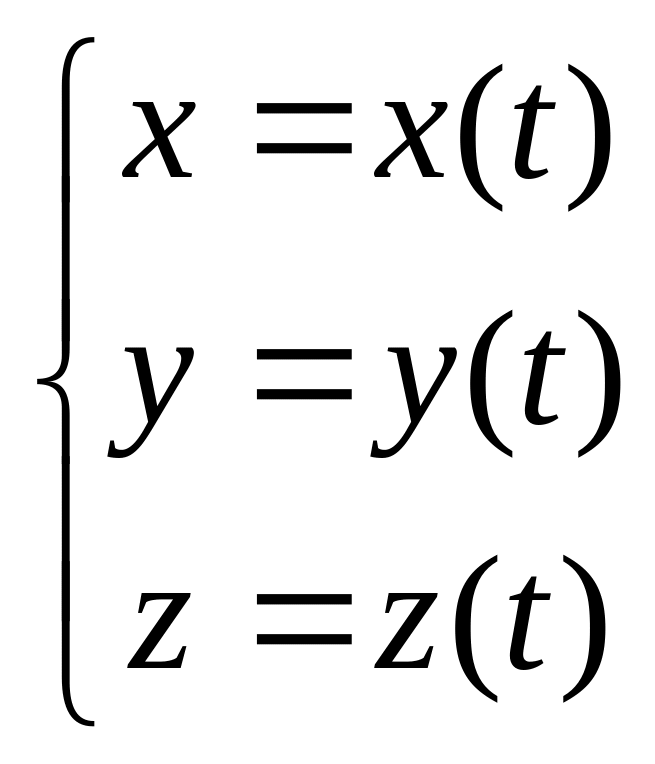
Параметрическое уравнение, где параметром является время (t).

Для того, что бы написать уравнение траектории, исходя из параметрических уравнений, необходимо исключить t.

Пример:

Пусть точка движется согласно уравнению

a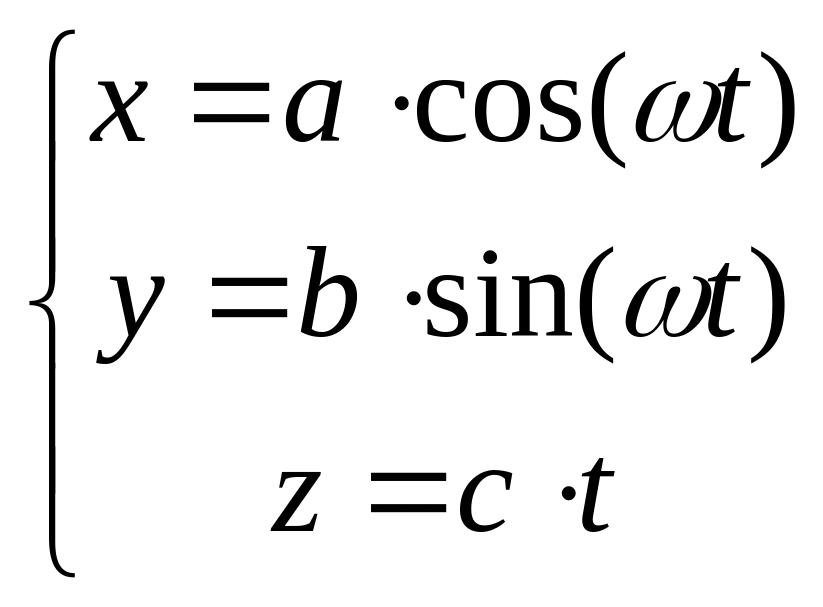 , b, c- постоянные, всегда положительные

t- время

Траекторией является спираль:

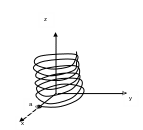
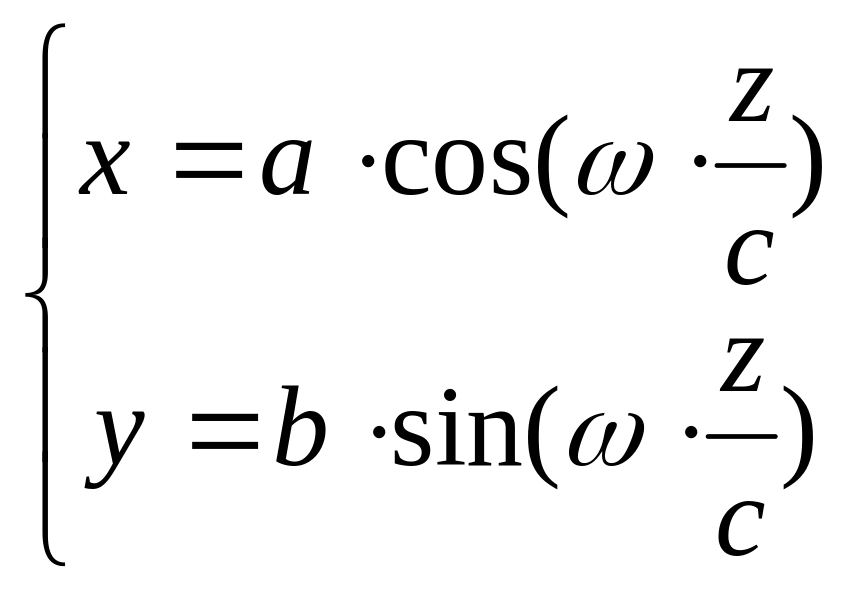
2) Естественный- задаётся кривая со стрелками по которым движется точка, стрелка показывает направление обхода кривой. Задаётся начало обхода по кривой, если точка движется по направлению стрелки, то S (путь) считается положительным, если точка движется против направления стрелки, то S отрицательный.

S=f(t)

П

S<0

уть равен ускоренному движению:

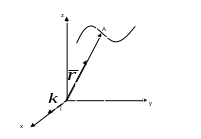
3) Векторный (главный) способ- задаётся система координат X,O,Y,Z траектория точки и вектор.

, где вектор функции.

Радиус вектор r, связан с осями x, y, z формулой

Для примера уравнения радиуса вектора можно использовать векторный способ:

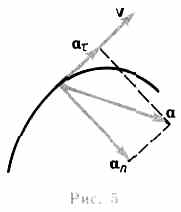
Скорость и ускорение

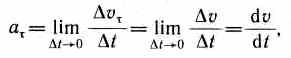
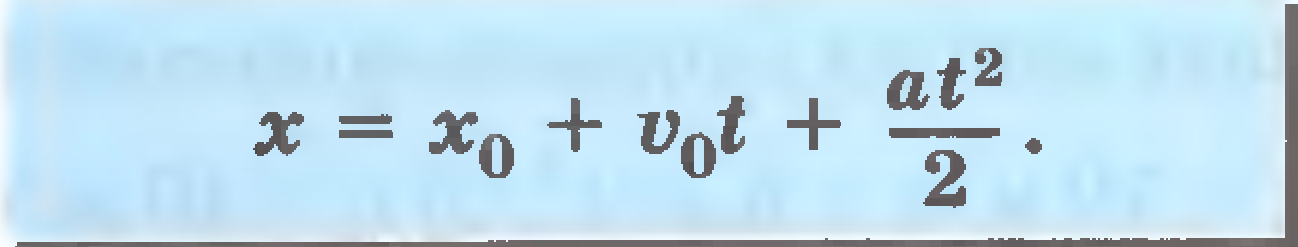
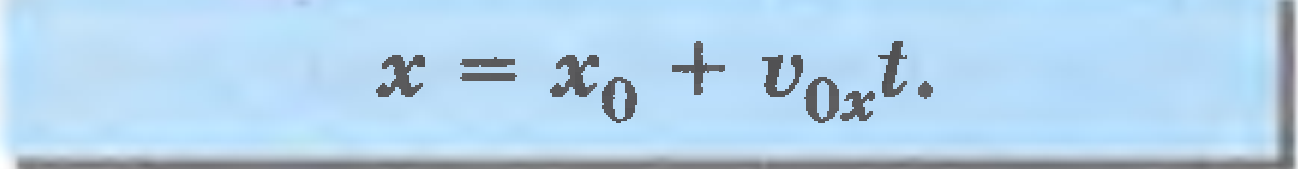
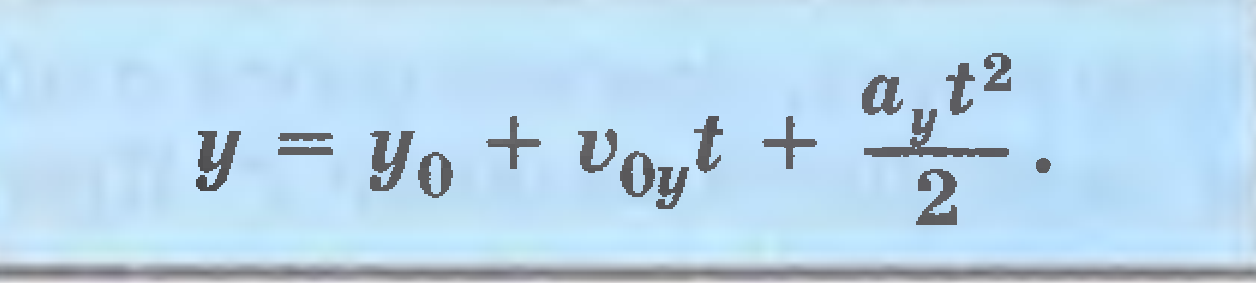
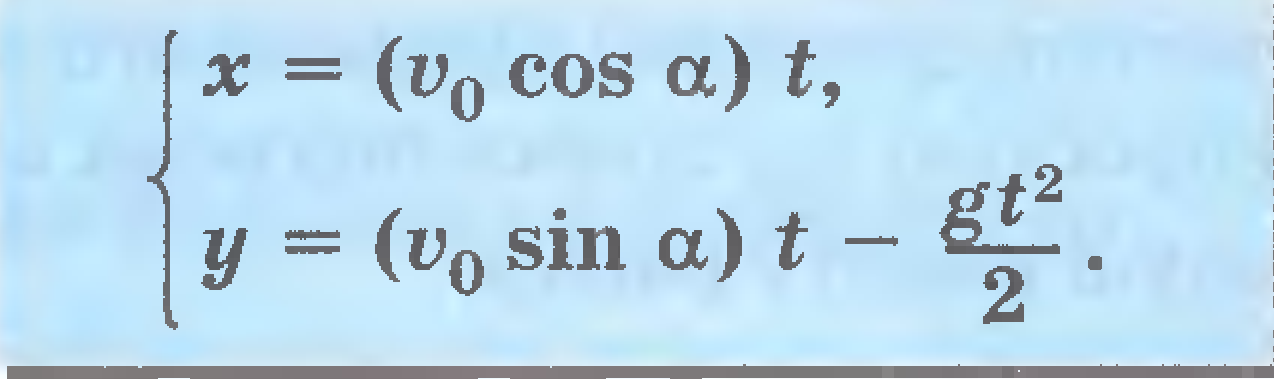
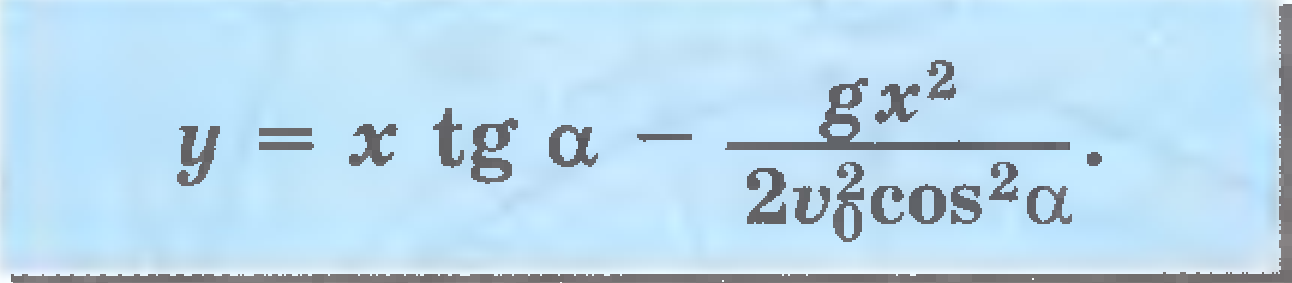
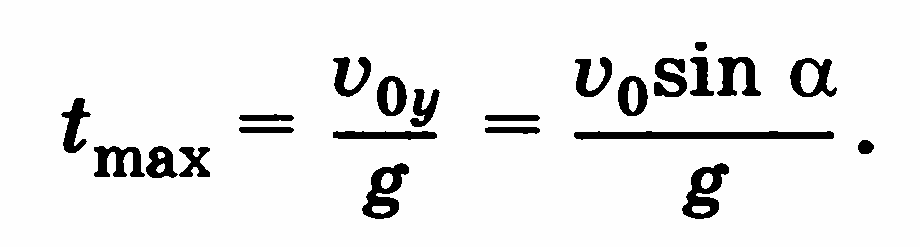
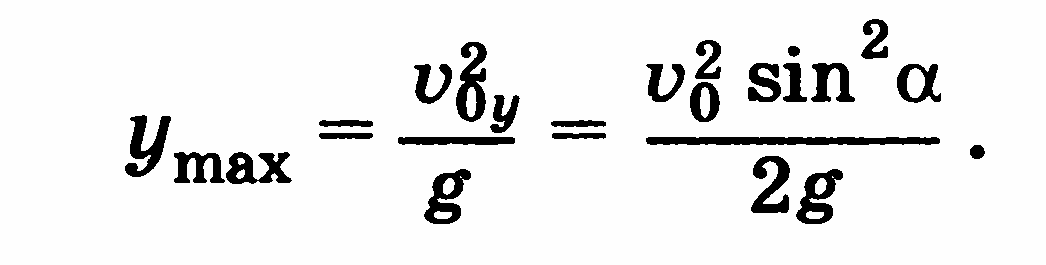
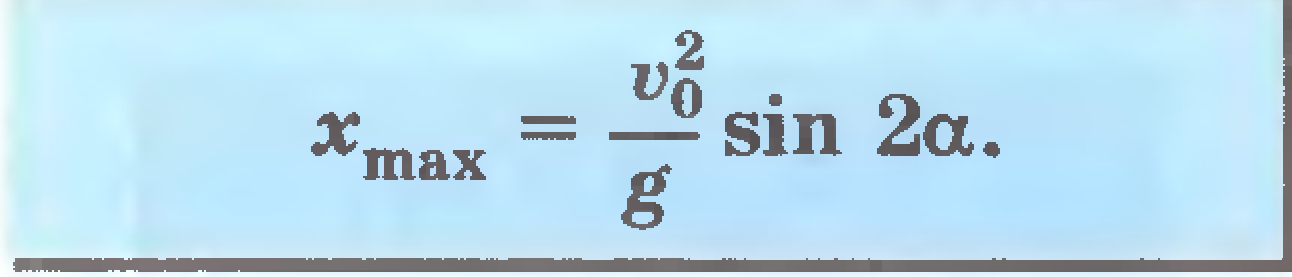2. 2. Динамика поступательного движения материальной точки и твердого тела.

Законы Ньютона. Принцип суперпозиции сил. Основные типы сил и взаимодействий. Механический принцип относительности. Механическая система. Центр масс системы материальных точек и закон его движения.

Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее ра­диус-вектор равен

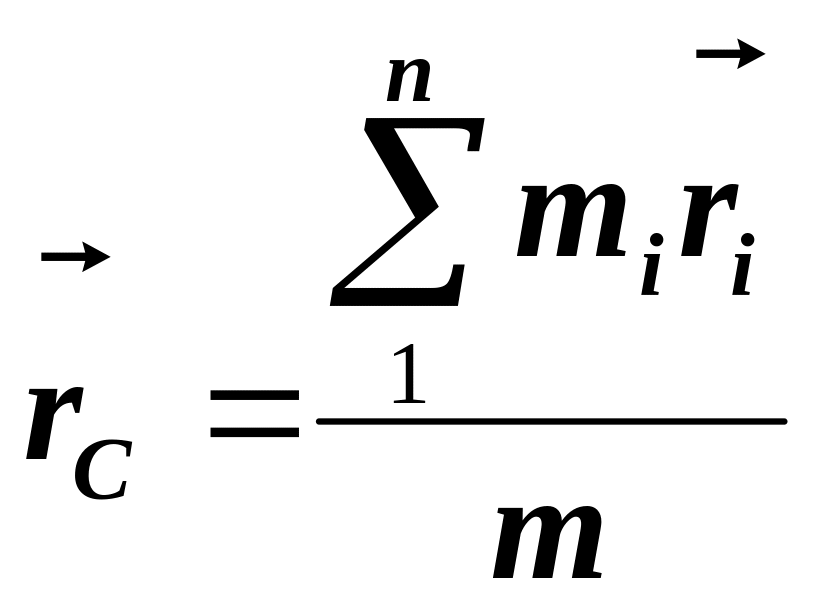
где m_i и r_i — соответственно масса и радиус-вектор i-й материальной точки; n — число материальных точек в системе; – масса системы. Скорость центра масс

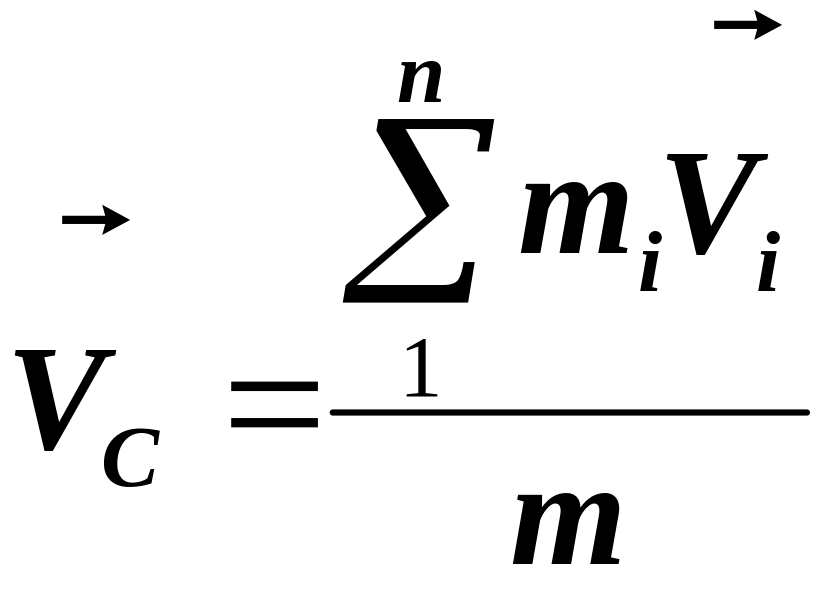
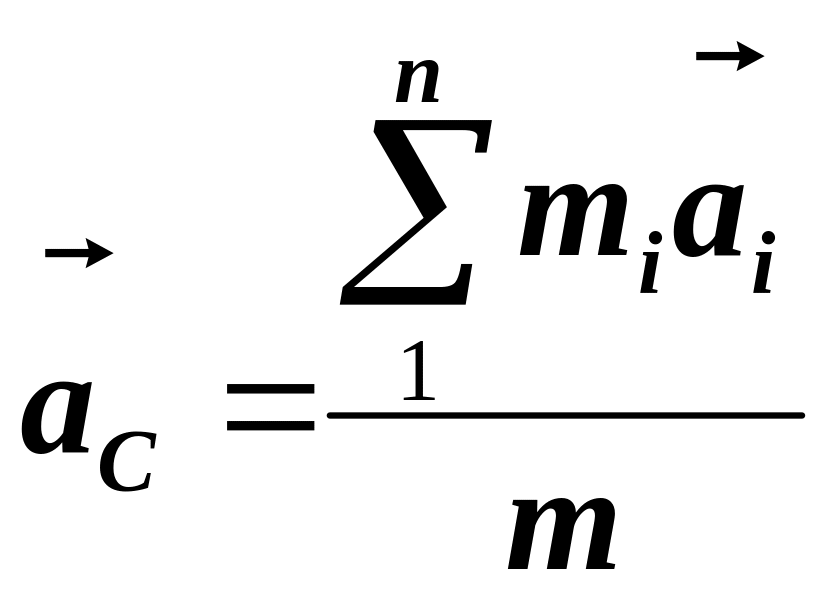
3.

3. Механическая работа. Кинетическая энергия. Потенциальная энергия. Законы сохранения в механике.

Определение и геометрический смысл работы. Работа силы. Работа силы тяжести и упругой силы. Связь работы с кинетической и потенциальной энергией. Движение точки в центральном поле. Закон сохранения.

Работа

Связь работы с кинетической и потенциальной энергией. Связь работы с кинетической энергией

= = = .

Связь работы с потенциальной энергией

Потенциальная энергия Условие потенциальности силового поля , оператор набла

Работа силы упругости, силы тяжести.

Сила упругости